1. 引言
视频会议网络系统是指各级保障机构的保障人员对所在单位范围内的人员或装备在训练、作战或演习过程中因指挥、控制与使用而产生的关联数据在节点流通中形成的一种网络。在实际作战过程中,各视频会议系统节点进入紧张有序的业务传输与吞吐,面对转瞬即逝的战机,个别节点会因时间紧、业务量大导致网络局部变得“脆弱”和“不堪”,随时面临“瘫痪”的风险。因此,如果能从网络全局考虑,对网络中传输的业务量进行合理规划和布局,合理调度、分配和优化各系统节点的传输业务,充分均衡各节点的业务处理时间,进而提高视频会议系统的作战保障效率 [1] [2]。该问题属于全局优化问题,即如何利用某种方法寻找全局最优解或者近似最优解,解决全局优化问题的方法有很多,本文选择模拟退火算法进行求解 [3] - [8]。
1982年Kirkpatrick等将固体退火过程引入大规模组合的全局优化领域,本文运用模拟退火算法解决视频会议网络系统的业务调度、分配和优化问题 [9] [10] [11]。
2. 模拟退火算法原理解析
对于某个固体,当使用一定的加热或其他手段让其温度达到很高程度,然后通过一定的降温方法逐渐降低其表面温度(即冷却过程):在温度抬升的过程中,根据分子运动理论,我们知道该固体的内部粒子的运动状态会无法捉摸,没有规律可循,同时粒子的能量会越来越大;但是冷却过程却恰恰相反,当该固体的温度慢慢降低时,其内部粒子的运动规律或状态则由高温状态下的无序变为低温状态下的有序,当达到常温状态时,粒子会达到一种状态,即基态,基态状态下的粒子能量达到最小 [12]。
Metroplis准则告诉我们,固体中的粒子在某一温度t时趋于有序或稳定状态的概率为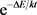 ,其中E为某一温度t时的粒子能量,
,其中E为某一温度t时的粒子能量,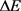 为粒子能量的变化值,k为玻尔兹曼常数 [13] [14]。
为粒子能量的变化值,k为玻尔兹曼常数 [13] [14]。
组合(最)优化问题是最优化问题的一类。我们可以借鉴模拟退火的原理去解决组合优化问题,即将粒子能量E设为目标函数值,而温度t为控制参数,模拟退火原理用算法描述如下 [15] [16] :
1) 设定某个参数变化区间,该区间可适用于模拟退火算法,同时设定目标函数的初值为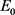 ;
;
2) 通过变化其中某个参数,得到一个新的目标函数值E,并且计算目标函数值的变化量,即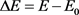 ;
;
3) 如果目标函数值的变化量 ,则目标函数值E被承认;如果目标函数值的变化量
,则目标函数值E被承认;如果目标函数值的变化量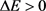 ,则目标函数值E被承认的概率为
,则目标函数值E被承认的概率为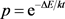 。并且当目标函数值E被承认后,
。并且当目标函数值E被承认后,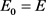 ;
;
4) 在某个温度值t下,重复步骤2)和步骤3);
5) 使温度t进一步降低;
6) 重复步骤2)和步骤5),直至满足函数收敛条件。
由模拟退火原理的算法描述,我们可以看出,结果收敛的关键因素取决于参数变化的初值和温度的衰减系数。
3. 问题的提出
现在有n种网络业务,这n种网络业务之间没有关联(即相互独立),需要某视频网络会议系统中m个节点对其进行加工处理,同时,这n种相互没有关联的网络业务所要求的网络性能和指标参数也不相同。与此同时,网络中各节点根据某视频会议系统保障的业务所到达的先后顺序,每次只能进行一种业务的信息处理,即完成输入输出的信息处理任务,每种业务所需的处理时间分别为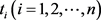 。现需要解决的问题是:为赢得战机,先敌一步夺得制信息权,如果各节点同时工作,怎么分配n种业务给视频会议网络系统节点,才能使节点处理所有业务的时间最短。
。现需要解决的问题是:为赢得战机,先敌一步夺得制信息权,如果各节点同时工作,怎么分配n种业务给视频会议网络系统节点,才能使节点处理所有业务的时间最短。
4. 具体解法
4.1. 问题描述
设有四种业务和三个网络节点,记集合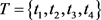 ,其中业务1和2要求平均网络延时和平均传送时间之和最小,业务3要求网络节点闲置率最小,业务4要求网络运行费用(即成本)最低。网络业务调度、分配和优化的目的是找出T中的三个不相交子集
,其中业务1和2要求平均网络延时和平均传送时间之和最小,业务3要求网络节点闲置率最小,业务4要求网络运行费用(即成本)最低。网络业务调度、分配和优化的目的是找出T中的三个不相交子集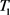 ,
,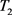 ,
,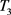 ,最终优化问题即为
,最终优化问题即为

由于平均网络延时、平均传送时间、网络节点闲置率、网络运行费用在网络节点业务调度中所占权重不同,因此这里采用AHP法算出权重系数。先建立四种性能指标的判断矩阵如表1所示:

Table 1. Judgment matrix of performance index
表1. 性能指标的判断矩阵
由表1,根据AHP法结算权重系数的方法:
第一步,求出判断矩阵的最大特征根对应的特征向量,即为评价指标的重要性排序。步骤如下:
1) 将矩阵每一列进行归一化处理:
 ,
,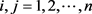 ,得到归一化矩阵
,得到归一化矩阵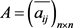 ;
;
2) 将归一化后的矩阵按行相加得: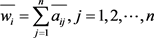 ;
;
3) 将列向量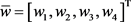 正规化处理:
正规化处理:
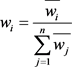 ,
,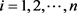
则 即为所求的特征向量。
即为所求的特征向量。
4) 计算矩阵的最大特征值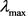 :
:
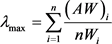
第二步,一致性检验:权重分配是否合理,需对判断矩阵进行一致性检验。
1) 计算判断的一致性检验指标C.I.有: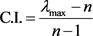 ;
;
2) 确定平均一致性指标R.I.,如表2所示。

Table 2. Random consistency index (R.I.)
表2. 随机一致性指标(R.I)
3) 计算一致性比例C.R.。C.R. = C.I/R.I.。当C.R. < 0.1时,认为判断矩阵的一致性是可以接受的。反之:
4) 当C.R. ≥ 0.1时,应该对判断矩阵作适当修正,以保持一定程度的一致性。
根据以上方法得出各权重系数为: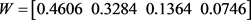 ,该判断矩阵满足一致性检验。则上述总优化目标可改为:
,该判断矩阵满足一致性检验。则上述总优化目标可改为:
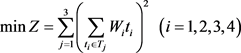
即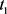 ——平均延迟时间,
——平均延迟时间,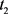 ——平均流通时间,
——平均流通时间,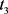 ——网络设备利用率,
——网络设备利用率,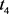 ——网络运行成本。
——网络运行成本。
这里我们采用排队论理论,即假设平均网络延时、平均传送时间均满足负指数分布,网络节点闲置率采用服务强度表示,网络运行费用由于某型视频会议系统网络节点业务处理过程中受各种因素影响,随时间变化,因此这里用随机数表示。
4.2. 模拟退火算法实现的主要步骤
1) 初始化 [17] [18] [19]
iter = 1; %迭代次数初值
a = 0.99; %温度衰减系数
t0 = 120;%初始温度
tf = 1;%最后温度
t = t0;
Markov = 10000; %Markov链长度
2) 模拟退火算法函数
function simulated annealing
N = 1; %迭代次数初始化
while t ≤ 0.001 %算法终止条件
for i = 1:Lk
f1 = fun(T1);
%约束参数的取值范围
T2(1) = exprnd(1.5); T2(2) = exprnd(2); T2(3) = 1-x2(1)/x2(2); T2(4) = rand;
%约束参数的取值范围
f2 = fun(x2);
if f2 − f1 < 0
T1 = T2; f(N) = f2; N = N+1;
else if exp((f1 − f2)/t) > rand
T1 = T2; f(N) = f2; N = N + 1;
end
t = t * a;
end
end
f1=fun(T1);
其中目标函数fun.m为:
function y=fun(T)
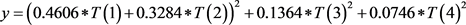
求得结果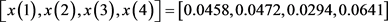 ,目标函数值为0.0018,这里的结果也是随时间变化的,解的变化如图1所示。
,目标函数值为0.0018,这里的结果也是随时间变化的,解的变化如图1所示。
5. 小结
由于模拟退火算法的本身特点,它毕竟只是一种随机算法,因此找到全局最优解的概率不会达到100%,只能确保找到近似最优解,而且运算起来比较快。同时,如果参数设置得当,模拟退火算法的搜索效率比穷举法要高 [19] [20]。