基于粒子群优化算法的股票指数追踪及投资分析

Stock Index Tracking and Investment Analysis Based on Particle Swarm Optimization Algorithm

摘要: 本文首先将二进制粒子群特征选择算法结合岭估计、Lasso估计和最小二乘估计利用成分股构建了三个关于上证50指数的指数追踪模型，三个模型都取得了非常优秀的追踪效果，其中无论是从追踪效果的角度还是投资角度出发，基于二进制粒子群特征选择算法结合最小二乘估计所得到的指数追踪模型都是最佳模型。然后利用三个指数追踪模型提取的成分股计算对上证50趋势的影响排名，其中贵州茅台的影响排名最高。最后在一定条件下进行投资行为的模拟和收益分析，发现基于三个指数追踪模型所提取的优质成分股进行投资可以获得比直接投资上证50指数更高的收益，达到了降低投资成本和投资风险的目的，为证50指数的投资提供科学合理的建议。

Abstract: In this paper, we first combine the binary particle swarm feature selection algorithm with ridge estimation, Lasso estimation and least square estimation to construct three index tracking models on SSE 50 Index using constituent stocks. The three models have achieved excellent tracking effects. The exponential tracking model based on binary particle swarm optimization feature selection algorithm and least squares estimation is the optimal model, whether from the perspective of tracking effect or investment. Then we use the constituent stocks extracted from the three index tracking models to calculate the impact ranking on the Shanghai Stock Exchange 50 trend, of which Kweichow Moutai ranks the highest, Finally, under certain conditions, the simulation and return analysis of investment behavior are carried out, and it is found that the investment of high-quality constituent stocks extracted based on the three index tracking models can obtain higher returns than direct investment in the SSE 50 Index, achieving the purpose of reducing investment costs and investment risks, and providing scientific and reasonable suggestions for the investment of the 50 Index.

1. 引言

近年来随着基金管理的日渐成熟，市场管理制度的不断完善，指数追踪 [1] 备受国内外投资者追捧。指数追踪的目的是从目标指数所包含的成分股中选择一组股票复制和跟踪目标指数的走势，从而获取与市场目标指数表现相近的收益，使得持有的股票与股指期货空单形成完全对冲以达到保值的效果。对于指数型基金管理者来说，常面临如何选取股票的问题，常见的方法有两种，分别是完全复制方法 [2] 和不完全复制方法 [3] 。若采用完全复制方法，则需购买目标指数的所有成分股票，根据每种成分股在目标指数中所占的权重来构建追踪组合，实现零误差复制目标指数收益率，但这种方法会产生较大的交易成本和高额的市场管理费用，特别是成分股较多的指数，如上证50指数包含了50只成分股，使用完全复制方法不符合实际；如果采用不完全复制方法，那么对上证50指数的优质成分股的提取及权重优化的分析与研究具有非常大的意义。本文将利用启发式粒子群优化算法 [4] 结合传统回归建模方法以最小化追踪组合走势和目标指数走势之间的误差获取优质成分股，以获得与指数差不多的收益率。虽然非完全复制方法存在一定的追踪误差，但投入的成本低，降低了投资风险，为较短期内投资者的投资选择提供合理可行的建议。

2. 数据介绍

本文研究数据来源于国内某证券交易网站，选取2021年6月10日至2023年5月31日上证50指数及其成分股日收盘价共479条数据作为研究对象。

上证50指数是上海证券交易所编制的一种综合指数，是从上市的所有股票中选取最具代表性的50只股票作为计算对象，并按成分股的调整股本数为权重进行加权计算得出的加权股价指数，其综合反映了上海证券市场最具市场影响力的一批龙头企业的整体状况。

本文研究的上证50指数成分股所属公司如表1所示：

Table 1. List of 50 constituent stocks on the Shanghai Stock Exchange

表1. 上证50成分股列表

3. 研究目的及分析流程

3.1. 研究目的

以上证50指数各成分股日收盘价作为自变量，优化成分股权重并构建上证50指数日收盘价的指数追踪模型，剔除不显著的成分股，最终提取出对上证50指数波动具有重要影响的优质成分股及其影响排名，并对其进行投资模拟分析，为上证50指数的投资提供科学合理的建议，减少投资者的交易成本和降低交易风险。

3.2. 分析流程

具体分析流程如图1所示。

第一步：通过通信达金融终端获取本文所研究的数据集，上证50指数及其成分股日收盘价。

第二步：将数据集按照时间先后顺序进行训练集(70%)和测试集(30%)划分。

第三步：将二进制粒子群特征选择算法分别结合岭估计、Lasso估计和最小二乘估计构建三个指数追踪模型并得到优质成分股。

第四步：对三个指数追踪模型的优质成分股进行影响分析并得到影响排名。

第五步：基于影响排名进行投资行为模拟并进行收益分析。

第六步：给出结论及投资建议。

Figure 1. Analysis flow chart

图1. 分析流程图

4. 研究方法

4.1. 多元线性模型

多元线性模型通常用来研究一个因变量依赖多个自变量的变化关系，如果二者的依赖关系可以用线性形式来刻画，则可以建立多元线性模型来进行分析与研究。

模型定义：

多元线性模型通常用来描述变量y与x之间的随机线性关系，即

$y={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_p{x}_p+\epsilon$ (1)

式中， $x_1,\cdots ,x_p$ 是非随机的自变量；y是随机的因变量； ${\beta }_0$ 是常数项； ${\beta }_1,\cdots ,{\beta }_p$ 是回归系数； $\epsilon$ 是随机误差项。

如果对y和x进行了n次观测，得到n组观测值 $y_i,x_{1i},\cdots ,x_{pi}\left(i=1,2,\cdots ,n\right)$ ，它们满足以下关系式

$y_i={\beta }_0+{\beta }_1{x}_{1i}+\cdots +{\beta }_p{x}_{pn}+{\epsilon }_i$ (2)

引入矩阵记号，记

$y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right],X=\left[\begin{array}{cccc}1& x_{11}& \cdots & x_{p1}\\ 1& x_{12}& \cdots & x_{p2}\\ ⋮& ⋮& \ddots & ⋮\\ 1& x_{1n}& \cdots & x_{pn}\end{array}\right],\beta =\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_p\end{array}\right],\epsilon =\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ ⋮\\ {\epsilon }_n\end{array}\right]$

则，模型(2)可以下位如下形式

$y=X\beta +\epsilon$ (3)

式中， $y$ 是观测向量； $X$ 是已知的设计矩阵； $\beta$ 是未知参数向量； $\epsilon$ 是随机误差向量。

如果模型(3)满足条件：1) $E\left(\epsilon \right)=0$ ，2) $Var\left(\epsilon \right)={\sigma }^{2}I$ ，3) $x_1,\cdots ,x_p$ 互不相关，则称模型(3)为普通线性回归模型。

在正态假定下，如果 $X$ 是列满秩的，则普通线性回归方程(3)的参数 $\beta$ 的最小二乘估计为：

$\hat{\beta }={\left(X^{{\rm T}}X\right)}^{-1}{X}^{{\rm T}}y$ (4)

于是得到回归方程

$\hat{y}=X\hat{\beta }$ (5)

4.2. 岭回归

1970年霍尔(Hoerl)和肯纳德(Kennard) [5] 提出了岭估计。可以有效解决传统回归模型在设计矩阵病态或者变量之间存在多重共线性时不再适用的问题。

考虑线性模型 $y=X\beta +\epsilon$ ，样本数据为 $y_i,x_{1i},\cdots ,x_{pi}\left(i=1,2,\cdots ,n\right)$ ，误差向量满足 $E\left(\epsilon \right)=0$ ， $Var\left(\epsilon \right)={\sigma }^{2}I$ ，假设这些样本是相互独立的，或者在给定 $x_{ij}$ 的情况下 $y_j$ 是独立的，同时也假设所有的 $x_{ij}$ 都进行了标准化处理，即

${\displaystyle \underset{j=1}{\overset{n}{\sum }}{x}_{ij}}=0,{\displaystyle \underset{j=1}{\overset{n}{\sum }}{x}_{ij}^2}=1$ (6)

可以通过解决如下条件极值问题获得

${\left(y-X\beta \right)}^{\prime }\left(y-X\beta \right)+k{\beta }^{\prime }\beta$ (7)

设 $\hat{\beta }={\left({\hat{\beta }}_1,\cdots ,{\hat{\beta }}_p\right)}^{\prime }$ ，则由(7)，岭估计其实就是使下式达到最小的参数估计

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-{\displaystyle \underset{j=1}{\overset{p}{\sum }}{\beta }_j{x}_{ji}}\right)}^2}+k{\displaystyle \underset{j=1}{\overset{p}{\sum }}{\beta }_j^2}$ (8)

其中k是拉格朗日乘数(Lagrangian Multipliers)，岭估计有如下表达式

$\hat{\beta }\left(k\right)={\left(X^{\prime }X+kI\right)}^{-1}{X}^{\prime }y$ (9)

其中 $k\ge 0$ 是岭参数。岭估计的分量 ${\hat{\beta }}_i\left(k\right)$ 作为k的函数，通过对k值的选择，可以减少多重共线性的影响，取不同的k值，可以得到不同的回归系数估计，因此岭估计 $\hat{\beta }\left(k\right)$ 是一个关于k的估计类。当k在 $\left[0,+\infty \right)$ 变化时，在平面直角坐标系所描出的图形称为岭迹，选择k的岭迹法是：将p个分量 ${\hat{\beta }}_i\left(k\right)$ 的岭迹画在同一个图上，选择k使得各个分量的值大致稳定，并且兼顾回归系数没有不合理的符号，残差平方和上升不太多等。当基于以上方法选择一个k值之后便可以得到岭估计 $\hat{\beta }=\left({\hat{\beta }}_1,\cdots ,{\hat{\beta }}_p\right)$ ，于是得到回归方程

$\hat{y}=X\hat{\beta }$ (10)

需要注意的是，当数据是标准化的时候有 $\bar{y}=0$ ，又有 ${\beta }_0$ 解 ${\hat{\beta }}_0=\bar{y}=0$ ，所以回归方程不含常数项。

4.3. 绝对约束估计

1996年蒂贝希拉尼(Tibashirani) [6] 提出了一种可以具有变量选择功能的估计方法——绝对约束估计(Lasso: the least absolute shrinkage and selection operator)。Lasso的基本思想是在回归系数的绝对值之和小于一个常数的约束条件下，使残差平方和最小化，从而能够产生某些严格等于0的回归系数，得到可以解释的模型，其等价于求下式达到最小值

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-{\displaystyle \underset{j=1}{\overset{p}{\sum }}{\beta }_j{x}_{ji}}\right)}^2}+\lambda {\displaystyle \underset{j=1}{\overset{p}{\sum }}\left|{\beta }_j\right|}$ (11)

其中 $\lambda \ge 0$ ，Lasso的复杂程度由λ，λ越大对变量较多的线性模型的惩罚力度就越大，从而最终获得更加简洁的模型。一般可以通过Cp准则、AIC准则、BIC准则和CV交叉验证得到最优λ下的最优回归模型。

4.4. 粒子群优化算法(PSO: Particle Swarm Optimization)

J. Kennedy和R. Eberhart [7] 等受到鸟类觅食的集群活动的启发而于1995年开发的一种演化计算技术.粒子群优化算法的思想是：假设空间中有一些粒子随机的分布在不同的空间位置上，每个粒子有两个属性——位置和速度。这两个属性的初始值都是随机的，位置代表了问题的解，而速度代表了每一次迭代中解的变化方向和快慢。在使用粒子群优化算法时，还要根据需要解决的问题设定合适的目标函数，根据目标函数可以计算出当前迭代为止每个粒子的最优解 $pbes{t}_i$ 以及所有粒子的全局最优解 $gbest$ 。每个粒子维护一个自身最优点 $pbes{t}_i$ ，整个粒子群维护一个全局最优点 $gbest$ 。然后进行迭代，迭代的过程可以描述为粒子按照自身最优 $pbes{t}_i$ 的方向和全局最优 $gbest$ 的方向按一定比例来改变速度，继而改变本次迭代粒子到达的位置。公式如下所示：

速度公式：

$v_i^{t+1}=w*v_i^t+c_1*rand1*\left(pbes{t}_i-x_i^t\right)+c_2*rand2*\left(gbest-x_i^t\right)$ (12)

其中 $w$ 、 $c_1$ 和 $c_2$ 为权重参数， $rand$ 是来自[0, 1]区间的随机数，t代表迭代次数，i代表第i个粒子。

位置公式：

$x_i^{t+1}=x_i^t+v_i^{t+1}$ (13)

位置公式就是简单的匀速直线运动公式(一次迭代相当于经过一个时间单位)。

4.5. 二进制粒子群优化算法(BPSO: Binary Particle Swarm Optimization)

粒子群优化算法是一个解决连续空间问题的算法，而要想应用到特征选择问题上需要做一些细微的修改以使它能解决离散空间问题。J. Kenedy和R. Eberhart在1997年开发出一个离散二进制版本简称(BPSO) [8] ，改进方法是速度公式不变，增加了一个二进制公式sigmoid函数，重新定义了位置公式。如下：

$x_{ij}=\{\begin{array}{l}1,rand<Sigmoid\left(v_{ij}\right)\hfill \\ 0,\text{otherwise}\hfill \end{array},Sigmoid\left(v_{ij}\right)=\frac{1}{1+{\text{e}}^{-v_{ij}}}$ (14)

经过二进制化后，粒子的位置x为仅包含0和1元素的向量，就具有了特征选择功能。 $gbest$ 中为1所对应的特征子集就是最终要选择的最优特征子集。

4.6. 模型评估指标

误差平方和(Sum of Squares due to Error, SSE)是在线性模型中衡量模型拟合程度的一个指标。模型的误差平方和越小表示模型拟合效果越好。其计算公式如下：

$\text{SSE}={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left({\hat{y}}_i-y_i\right)}^2}$ (15)

平均绝对误差(Mean of Absolute Error, MAE)描述了真实值与预测值之间误差的均值，因而可以准确反映实际预测误差的大小。模型的平均绝对误差越小表示模型拟合效果越好。其计算公式如下：

$\text{MAE}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|{\hat{y}}_i-y_i\right|}$ (16)

平均相对误差(Mean of Relative Error，MRE)指相对误差的平均值，这个平均相对误差一般是用绝对值，平均相对误差更能反映预测的可信程度，相对误差一般以百分数的形式进行表示。模型的平均相对误差越小表示模型拟合效果越好。其计算公式如下：

$\text{MRE}=\frac{100}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{\left|{\hat{y}}_i-y_i\right|}{y_i}}$ (17)

风险误差(Risk Error, RE)衡量了模型的预测稳定性。模型的风险误差越小表示模型预测效果更加稳定。其计算公式如下：

$\text{RE}=\sqrt{\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(\left({\hat{y}}_i-y_i\right)-\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left({\hat{y}}_i-y_i\right)}\right)}^2}}{n-1}}$ (18)

5. 实证分析

5.1. 划分训练集和测试集

本文所研究股票数据属于时间序列类型数据，为了更好的对上证50指数构建回归模型进行指数追踪，需要将数据按照时间先后顺序进行训练集(70%)和测试集(30%)划分，其中2021年6月10日至2022年10月28日共336条数据作为训练集，2022年10月31日至2023年5月31日共143条数据作为测试集。以训练集构建上证50指数追踪模型，利用测试集对指数模型进行质量评估。

5.2. 岭回归结合BPSO

在构建岭回归方程之前需要确定参数λ，λ的确定现在已经有了很多相对比较成熟的方法。本文基于广义交叉验证GCV [9] 最小值来确定岭回归建模时所使用的λ值。

本文首先利用向后选择法逐步剔除不显著的自变量，剔除的原则是：每次剔除最不显著的自变量，即剔除检验统计量绝对值最小或者P值最大所对应的自变量，直至剩余的自变量对因变量都有显著的影响为止。然后基于最小化岭回归模型在测试集预测误差下，结合二进制粒子群优化算法对剩余成分股进行变量筛选，最终共剔除24只成分股。最后利用剩余成分股构建关于上证50指数的岭回归方程如下所示：

$\begin{array}{l}\hat{y}=185.504-0.149x_1+0.684x_2+0.680x_3+0.795x_7+\cdots \\ +0.435x_{43}+8.600x_{44}-0.341x_{45}+5.980x_{48}+2.516x_{49}\end{array}$ (19)

利用该回归方程可以得到基于BPSO特征选择之后的岭回归模型的模型检验结果如表2所示：

Table 2. Testing results of ridge regression model

表2. 岭回归模型的检验结果

模型在测试集上各评价指标值如表3所示：

Table 3. Evaluation results of ridge regression model

表3. 岭回归模型的评估结果

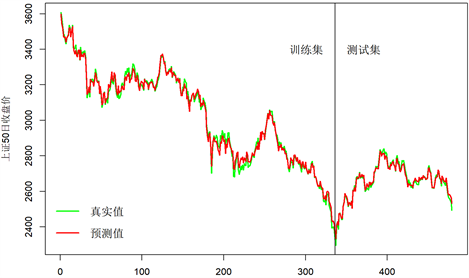
Figure 2. SSE 50 Index tracking chart of ridge regression model

图2. 岭回归模型的上证50指数追踪图

从表2的模型检验结果可以发现，岭回归指数追踪模型通过了显著性检验同时解释了成分股和上证50指数之间绝大部分的线性关系。从表3的模型评估结果以及图2指数追踪图可以发现，基于二进制粒子群优化算法和岭估计所得到指数追踪模型是本文所构建的三个指数追踪模型中追踪能力和稳定性最差的，但就该模型而言其MRE指标为0.3826，表明平均预测误差为真实值的0.3826%，同样也展现了非常良好的指数追踪能力。

5.3. Lasso回归结合BPSO

在构建Lasso回归方程之前需要确定参数λ，Lasso回归方程复杂度由参数λ来控制，λ越大对变量较多的线性模型的惩罚力度 [10] 就越大，从而最终获得一个更加简约的模型。λ的确定现在已经有了很多相对比较成熟的方法。本文基于CV交叉验证法来确定Lasso回归建模时所使用的λ值，由此可获得自变量的回归系数估计值，对于回归系数为0的自变量认为其对于上证50指数日收盘价的影响不够显著，作出剔除处理。

本文首先利用Lasso估计自带的变量选择功能剔除回归系数估计为0的成分股。然后基于最小化Lasso回归模型在测试集预测误差下，结合二进制粒子群优化算法对剩余成分股进行变量筛选，最终共剔除25只成分股。最后利用剩余成分股构建关于上证50指数的Lasso回归方程如下所示：

$\begin{array}{l}\hat{y}=141.1074+0.6692x_1+0.6703x_2+0.3809x_3+2.0402x_5+\cdots \\ +7.6016x_{44}+2.2725x_{45}+1.6886x_{47}+10.5601x_{48}+0.0058x_{50}\end{array}$ (20)

利用该回归方程可以得到基于BPSO特征选择之后的Lasso回归模型的模型检验结果如表4所示：

Table 4. Testing results of lasso regression model

表4. Lasso回归模型的检验结果

模型在测试集上各评价指标值如表5所示：

Table 5. Evaluation results of lasso regression model

表5. Lasso回归模型的评估结果

Figure 3. SSE 50 Index tracking chart of Lasso regression model

图3. Lasso回归模型的上证50指数追踪图

从表4的模型检验结果可以发现，Lasso回归指数追踪模型通过了显著性检验同时解释了成分股和上证50指数之间绝大部分的线性关系。从表5的模型评估结果以及图3指数追踪图可以发现，基于二进制粒子群优化算法和Lasso估计所得到的指数追踪模型的指数追踪能力和稳定性在三个模型中都处于中间水平。

5.4. 最小二乘回归结合BPSO

本文首先利用向后选择法逐步剔除不显著的自变量，剔除的原则是：每次剔除最不显著的自变量，即剔除检验统计量绝对值最小或者P值最大所对应的自变量，直至剩余的自变量对因变量都有显著的影响为止。然后基于最小化最小二乘回归模型在测试集预测误差下，结合二进制粒子群优化算法对剩余成分股进行变量筛选，最终共剔除17只成分股。最后利用剩余成分股构建关于上证50指数的最小二乘回归方程如下所示：

$\begin{array}{l}\hat{y}=136.7298+0.5166x_1+0.4954x_4+0.8881x_5+0.6115x_7+\cdots \\ +4.4490x_{44}+1.5898x_{45}+4.2222x_{46}+1.9406x_{47}+0.1668x_{49}\end{array}$ (21)

利用该回归方程可以得到基于BPSO特征选择之后的Lasso回归模型的模型检验结果如表6所示：

Table 6. Testing results of least squares regression model

表6. 最小二乘回归模型的检验结果

模型在测试集上各评价指标值如表7所示：

Table 7. Evaluation results of least squares regression model

表7. 最小二乘回归模型的评估结果

Figure 4. SSE 50 Index tracking chart of least squares regression model

图4. 最小二乘回归模型的上证50指数追踪图

从表6的模型检验结果可以发现，最小二乘回归指数追踪模型通过了显著性检验同时解释了成分股和上证50指数之间绝大部分的线性关系。从表7的模型评估结果以及图4指数追踪图可以发现，各项模型评估指标值在三个模型中都是最小的，说明基于二进制粒子群特征选择算法结合最小二乘估计所得到的指数追踪模型的指数追踪效果最佳。

5.5. 成分股影响分析

为了到达利用少数的成分股便可实现对指数的追踪，即在使用更少的成本去投资少数几个优质股票尽可能获得接近于直接投资上证50指数所获得收益并降低投资风险的目的，需要讨论各成分股对于上证50指数的影响程度。最终是要提取出能够准确及时反映上证50指数日收盘价趋势的成分股即所谓的优质股票。

成分股对指数日收盘价波动大小的影响，通常会使用回归系数来衡量，但回归系数仅仅只描述了成分股日收盘价对指数日收盘价贡献的权重大小。一只高回归系数的成分股可以表明在指数日收盘上有更大的权重作用，但如果该成分股的波动变化比较小，那么最后对于指数日收盘价波动的组成占比也不会太大。所以在考虑回归系数的基础上同样还考虑成分股方差的大小，两者结合来衡量成分股对指数收盘价波动的影响。本文将使用以下公式计算成分股对指数日收盘价波动的影响大小：影响系数 = 回归系数*成分股日收盘价方差，为了更好的比较不同模型下各个成分股对指数日收盘价的影响，再对影响系数进行0~1区间标准化，同时为了更好的展示各成分股的影响系数，对各成分股的影响系数同时乘上100。

基于三个指数追踪模型计算各成分股影响系数如下：

基于岭回归模型计算各成分股影响系数如表8所示：

Table 8. The influence coefficient of component stocks in ridge regression model

表8. 岭回归模型的成分股影响系数

虽然在构建岭回归模型的过程中已经剔除了不显著的变量，但是从上表还是可以发现某些成分股对于上证50指数日收盘价的走势不够敏感，比如中国神华、天合光能、保利发展和中国石化这些股票的影响系数是远远小于排名靠前的股票影响系数。

基于Lasso回归模型计算各成分股影响系数如表9所示：

Table 9. The influence coefficient of component stocks in lasso regression model

表9. Lasso回归模型的成分股影响系数

虽然在构建Lasso回归模型的过程中已经剔除了不显著的变量，但是从上表还是可以发现某些成分股对于上证50指数日收盘价的走势不够敏感，比如包钢股份、中国建筑、中国石油和国电南瑞这些股票的影响系数是远远小于排名靠前的股票影响系数。

基于最小二乘回归模型计算各成分股影响系数如表10所示：

Table 10. The influence coefficient of component stocks in least squares regression model

表10. 最小二乘回归模型的成分股影响系数

虽然在构建最小二乘回归模型的过程中已经剔除了不显著的变量，但是从上表还是可以发现某些成分股对于上证50指数日收盘价的走势不够敏感，比如国电南瑞、中国石化、三峡能源和中国建筑这些股票的影响系数是远远小于排名靠前的股票影响系数。

从上述三个模型所得到的成分股影响系数结果来看，各个模型所得到的结果都有所差异，但有一个共同点就是贵州茅台的影响系数在三个模型结果中都是最高的。

5.6. 投资行为模拟及收益分析

在上述内容中利用各个回归模型提取出了优质成分股影响排名的情况下，本文将在此基础上进行投资行为模拟和收益分析，以判断上述所得到的优质成分股是否能够达到本文想要研究的目的。

在投资行为中，有一个比较简单的核心思想：在暴跌之前卖出，在暴涨之前买入。基于以上思想本文主要以图5中所示的上证50指数波动比较大的三个区间来进行投资行为模拟。

Figure 5. Investment interval

图5. 投资区间

图5标示出了[51, 124]、[213, 256]、[337, 396]三个区间，[51, 124]区间表示样本51 (时间2021/8/23)到样本124 (时间2021/12/10)这段范围，这三个区间都是上证50指数暴跌后强势反弹的一个区间。本文将以这三个区间为例，分析投资优质成分股票和直接投资上证50指数所带来的收益对比。

现给出三个前提条件：

1) 以50万为投资金额。

2) 可以以分数的形式购买相应份额的股票(各成分股投资金额是基于影响系数进行分配，所以不满足购买整数份额的股票)

3) 成分股投资上，选择影响排名前K (K = 5, 10, 15, 20)四种情况的成分股进行投资

在以上三个前提条件下给出以下模拟步骤：

1) 资金分配：以各成分股的影响系数为比重分配50万资金为各自成分股投资资金；以50万资金作为上证50的投资资金

2) 买入：将各成分股和上证50的投资资金除以上述3个区间的初始时刻(上证50日收盘价处于谷底)各自日收盘价得到各个成分股和上证50的买入份额

3) 卖出：将第三步所获得的各成分股和上证50的份额乘以上述3个区间的末时刻(上证50日收盘价处于顶点)各自日收盘价得到各个成分股和上证50的收益。

4) 将各个成分股所得收益求和得到投资成分股所得收益并减去原始投资资金50万得到最终净收益，与直接投资上证50指数所得净收益进行比较。

经过上述的模拟之后得到三个模型下的投资结果如表11所示：

Table 11. Income statement

表11. 收益表

注：红色代表横向数据最大值(净收益收益最大)。

从表11可以得出如下结论：

1) 从投资净收益的角度来看，三个指数追踪模型分别所提取的影响排名前5、10、15和20优质成分股在三个区间的投资净收益都高于直接投资上证50指数所获得的净收益。

2) 基于岭回归、Lasso回归和最小二乘回归所提取的优质成分股中，投资影响排名越靠前的成分股所获得的净收益越多。

3) 无论是选择影响排名前5、10、15还是20的成分股进行投资时，基于最小二乘回归指数追踪模型所得到的净收益是三个指数追踪模型中最高的。

4) 选择影响排名前5,、10、15和20的成分股进行投资时，基于三个指数追踪模型所得到的净收益以及净收益之间的差额都呈现一定的递减趋势。

5) 就本文所模拟的投资行为而言，基于最小二乘回归指数追踪模型所得到的净收益平均高出直接投资上证50指数所得净收益约180,000元。

6. 总结与建议

6.1. 总结

本文研究分析了2021年6月10日至2023年5月31日上证50指数及其成分股日收盘价的情况，构建了各成分股与上证50指数之间的回归模型，利用回归模型探讨了各成分股对上证50指数趋势及波动的影响，提取了各成分股中的优质股票并进行影响排名，经过投资行为模拟和收益分析证实三个指数追踪模型各自所提取的优质成分股是有效的，能够在相同投入资金下获得比直接投资上证50指数更高的净收益，并且在投资成分股的选择下具有更大的灵活性和风险性控制。

首先基于二进制粒子群优化算法结合岭估计、Lasso估计和最小二乘估计进行成分股选择，筛选出了优质成分股，成功构建了关于上证50指数的岭回归指数追踪模型、Lasso回归指数追踪模型和最小二乘回归指数追踪模型。三个指数追踪模型中最小二乘回归指数追踪模型的拟合能力、预测能力和稳定性都是最优秀的，岭回归指数追踪模型的拟合能力、预测能力和稳定性都是最差的，但三个指数追踪模型都表现出了非常优秀的指数追踪能力。

然后基于三个回归模型所提取的成分股利用影响系数衡量了各个成分股对于上证50指数波动的影响并进行了影响排名，三组回归模型所提取的成分股都有所差别，但是从影响排名来看，三组回归模型的成分股影响排名中，排名最高的都是贵州茅台。

最后利用三组成分股影响排名进行了投资行为模拟并分析了收益情况，三个指数追踪模型各自所提取的优质成分股是有效的，能够在相同投入资金下获得比直接投资指数更高的净收益。相同投资资金下，选择越多的优质成分股进行投资，其获得的净收益一般来说会越低，但是其风险也会越低。其中无论是从追踪效果的角度还是投资的角度出发，基于二进制粒子群特征选择算法结合最小二乘估计所得到的指数追踪模型都是最佳模型。

6.2. 建议

1) 可以选择最小二乘回归指数追踪模型所提取的优质股票进行投资，就模拟投资而言，其带来的净收益最高。同样也可以基于三个指数追踪模型进行组合投资。

2) 追求高收益情况下，可以选择排名靠前的少数几只优质成分股进行投资，相对的也会带来更高风险。

3) 追求稳定的话，可以选择更多的优质成分股进行投资以降低风险性。

4) 本文主要研究是提取上证50指数优质成分股及其影响排名，在可靠的消息和经验支持下在未来一段时间上证50指数有一定的上涨趋势，再结合本研究所提取的优质成分股可能才会取得预期的收益。

5) 本研究旨在分析各成分股与上证50指数之间的关系以及提取优质成分股，为关于上证50指数的投资提供科学合理和可靠的方向和策略。并非单靠这份简单的分析报告就可以获得预期的收益，应当学习相关知识以及在大量经验和可靠信息下才能涉及投资领域。