1. 引言
国内最早提出数学美 [1] 这个概念的人是徐利治先生。后续很多学者对数学美主要从对称美、和谐美等方面进行论述,这些当然也是很有意义的研究,不过,数学教育所追求的并不仅仅是形式美的描述,更重要的是在数学教学过程中如何展现数学美。
2. 教学逻辑的提出
2.1. 概念的提出
作为一名数学教育工作者,基本都考虑过这样的问题:怎么上好一节课?究竟要教给学生什么样的数学?为什么要学习数学这门课?教师传授数学知识本身当然很重要,同时这些知识背后所渗透的思想方法更为重要,然而更有价值的是研究数学问题的科学精神。数学教育想要让学生领会到数学知识背后更深层面的东西——数学教育的本质,只有思维。让学生真正学会思考、乐于思考,进而具备逻辑性思维,才是数学教师存在的真正意义。然而对于大多数初学者来说,知识内容生疏,体系建构不完整,思考问题不全面,这就需要老师进行适度的引导教学,于是就有了教学逻辑。通过教学逻辑,让学生真正体会数学的“内在美”。
2.2. 目前教学存在的问题
逻辑是教学关系结构优化的重要因素,教学逻辑的好坏直接影响教学系统内部各环节的分布与平衡,并且对教学效果和教学质量产生明显的差异。目前的课堂教学现象大都存在这样的问题:听某位教师的课,整个讲课的过程虽然挑不出什么毛病,但总觉得少了点什么东西,或者说失去了一些味道,感受不到贯穿整节课教学的一条主线。还有一些课,整个教学设计似乎也没什么问题,讲课的过程也规范,也没有出现教学知识科学性的错误,但是结果就是听课的人提不起任何兴趣,过程过于枯燥、乏味。也存在这样的课堂,教师整节课都以教学知识为目标,过程单调乏味。其实上述的教学现象产生的根本原因在于缺失教学逻辑,一堂“生动”的课堂是教学逻辑贯穿整个过程,因为教学逻辑是课堂教学的灵魂。
3. 教学逻辑的内涵
那到底什么才是教学逻辑呢?发展至今,对其解释有很多。朱德全和张家琼是国内早期对教学逻辑做系统研究阐述的学者,他们把教学比作复杂多变的网络组织系统和关系互动系统,教学逻辑则作为教学系统的子系统,承担着系统内部教学主客体关系的动态转化和逻辑推进 [2]。后续的研究均是在他们研究的基础之上进行更新,如郑长龙与历晶提出,任何课堂均由学生、教师、内容这三个要素组成,其内在的思维逻辑组成了教学逻辑的静态结构,即学科逻辑、学的逻辑和教的逻辑,并且揭示了其内在联系与转化 [3]。后来董静等人表示“教学逻辑是教师基于对学科教学与学生发展关系认知基础上形成的关于教学内容与教学活动序列安排的构想” [4]。直到郑慧敏等人提出教学逻辑的概念模型(图1) [5],教学逻辑的内容也越来越丰富。从以上研究我们可以得出:教学逻辑主要包含了两方面的内容,一方面是静态的内容,包括学科知识本身的内部逻辑关系,即学科的逻辑;另一方面是动态的内容,包括教师教的活动,学生学的活动,总归思维活动。所以笔者在本文中对于教学逻辑概念的定义主要包含两方面的内容,即学科逻辑与思维逻辑,其内部的逻辑关系如下(图2)。
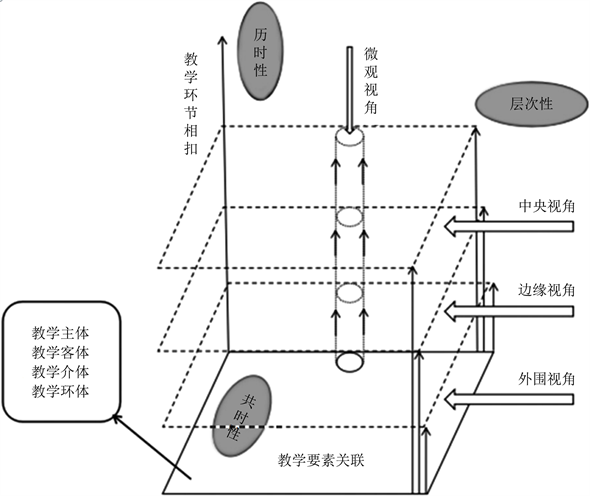
Figure 1. Conceptual model of classroom teaching logic
图1. 课堂教学逻辑的概念模型
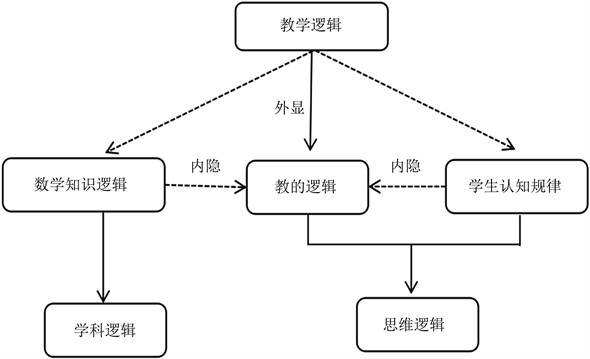
Figure 2. The constitutive relation of teaching logic
图2. 教学逻辑的结构关系
东北师范大学高夯教授曾说过:要做一名好的教师,就要“想明白、说清楚”。这六个字其实也诠释了教学逻辑的涵义,笔者认为这六个字均有两层涵义,一是对于教师来说,“想明白”首先教师自身得准确掌握学科内容之间的逻辑关系,即所讲的知识与前后知识之间的逻辑关系,以及知识本身在学科中的价值与地位;其次要明白所传授知识的实际意义是什么?为什么我们要学它?学习它对我们有什么用?最后,教师要明确数学教育的价值基础上,掌握研究问题的科学精神,因为数学传授的不仅仅是知识,更重要的是方法,一种研究问题的精神。要想成为一位优秀的教师,在每次上课之前都要认真思考:这节课的价值是什么?这节课我需要教给学生什么知识?只有真正了解数学教学的意义与价值,这才是真正意义上的想明白。想要做到这一点,只有在实践的教学研究中,通过不断的探索,明晰数学教学的教育价值,才能真正的掌握教学逻辑。“说清楚”是指教师在洞悉数学教育的本质与价值下,引导学生深刻理解所要学习的数学知识,体会数学知识包含的思想方法,让学生感受教师的思维主线,遇到问题,怎么去研究问题,要做到这一点,需要教师在深刻理解学科逻辑的基础上进行富有成效的教学活动,并且设置的问题也能够准确的揭示数学知识的本质,即“提好”问题。另一个层面是对学生来说:教师所面对的是学生,每个学生都是独立的个体,他们拥有自己独特的认知与思维,因此教学的过程是思维碰撞的过程。然而在实际教学中,都忽视了学生自身学科逻辑与思维逻辑的确立,只是填鸭式地灌输具体操作,没有留时间让学生自己体会知识的来龙去脉,这样的教学与数学教育的本质是背道而驰的。作为教师,其任务就是将人类发展的精华即科学知识,通过教学内化成学生的精神财富,成功的教学就是看到学生的进步与发展。因此在教学中,教师一方面要站在学生的角度去感受、理解所教授的学科逻辑,考虑到学生可能会遇到的问题,另一方面能够站在思维逻辑的高度理解数学知识,挖掘知识背后的思维规律,那么就应该注意所提的问题要有助于学生学科逻辑与思维逻辑的确立,并且可以有效地激发学生的思维活动,即提“好的”问题,来帮助学生“想明白”,这样学生才能够真正的“说清楚”。
因此,作为一位数学教师,首先要自己明白每个知识点的逻辑,说清楚教学过程中的思维逻辑,然后在符合数学学科逻辑与学生认知发展规律的基础上,通过开展有效的教学活动,引导学生想明白来丰富自身的知识结构体系,说清楚进而发展自身的思维逻辑,提升探究问题的一般方法。
4. 教学逻辑在教学中的应用
4.1. 学科逻辑
教学逻辑首先讲的是学科逻辑,而学科逻辑主要是指“教什么”。数学上的许多东西,只有认识到它的正确性,才能感觉其“美好” [6]。数学教学均是以知识为载体进行教学,知识之间往往存在一定的逻辑关系,只有充分掌握其正确合理的逻辑关系,才能有效地帮助学生理解知识。
以人教A版高中数学必修一中第三章函数的概念与性质为例(如图3)。我们学习数学知识首先要清楚它的价值,体会它的意义。必修1是学生从初中进入高中的第一本数学教材,它衔接了初中数学知识,又为高中后续的教学拉开帷幕,奠定基础。初中已经学习了一些有关函数的知识,只是初中函数概念从描述性的变量观点来解释,其效果也易于学生的理解,纵观世界的发展进程,随着社会的发展,认识会深化,任何理论的发展都必然会走向符号化与抽象化,这也是数学这门学科发展的一般规律。所以我们可以看到第一章先引入集合的概念,为函数概念上升到符号化与抽象化提供工具。在第三章教材内容的开头用一段引言大概描述了函数在现实生活中的应用,让学生了解数学其实是对现实生活抽象,并不是纸上谈兵,空中楼阁。接着通过现实生活中四个问题给出变量与函数关系,让学生通过观察,用集合的语言刻画出函数概念以及要素。然后又在初中知识的基础上给出函数的三种表示方法,来加深对函数概念的认识。了解了函数的表达方式,接着就是研究函数的性质,最后通过幂函数的学习感受函数的整个研究过程,并且学会理解和解决现实中的问题。我们可以看到,本章节整体内容的安排逻辑是合理的,但是一些细节安排还是有待商榷的。

Figure 3. Knowledge structure of function concepts and properties
图3. 函数概念与性质知识结构
例如第三章第二节中函数的单调性研究,教材上我们可以看到这样的描述(如图4),对于二次函数的单调性研究,首先画出函数图形,因为图形左侧是下降的,所以y随x的增大而减小,接着用符号语言进行验证,而此处的符号描述即函数的解析式,图像右侧性质同理。此描述似乎在告诉我们函数的性质是由函数图形决定的,后续应用函数的解析式进行验证,那我们不禁问函数的图像是怎么来的呢?显然上述描述的学科内容逻辑是不对的。函数性质的本质是随着自变量的变化,因变量的特征属性,如果函数自变量在定义域内由小到大的变化,因变量也随着由小到大或者由大到小的变化,这便是函数的单调性。此性质对应在图像上,如果图形从左至右是向下的,那么此函数的图像特征就是单调递减的,若函数图像从左至右是向上的,则此函数的图像特征就是单调递增的。在研究函数奇偶性时,首先不是引导学生观察函数图像的对称性,而是让学生分析其解析式。例如y = a3,使学生从自变量a与因变量y的关系去感受函数的整体性质,也就是当函数y = a3自变量取相反数,即a和−a的时候,函数y = a3对应的函数值相反,即a3和−a3。此性质对应在图像上,两个点的横坐标关于原点0对称,其对应的纵坐标互为相反数,所以就可以得到函数图像关于原点0对称。只有让学生对函数的对称性有理性认识,后续也就不难理解函数y = (x − 2)2 − 6的图像为什么关于x = 2对称了。因此可以得出,函数解析式决定函数的性质,函数图像是由函数的解析式而来的,图像的特征只是对解析式所推导的性质进行验证而已,图4所描述的学科逻辑刚好相反。
人教版八年级下册第十九章中一次函数的教学也有类似的描述(如图5),可以看到一次函数的性质是通过描点得到的图形看出来的,这与函数性质研究的学科内容逻辑是背道而驰的。函数图像来自其解析式,两者是一一对应的,很多时候为了研究方便,我们经常借助函数图形进行分析研究函数性质,但是一定要明晰函数解析式中自变量与因变量的关系才是研究函数性质的关键,尤其是在函数性质初教学时,务必帮助学生建立正确的学科逻辑。

Figure 4. High school mathematics compulsory one chapter 3 of People’s Education A Edition
图4. 人教A版高中数学必修一第三章

Figure 5. Chapter 19, Grade eight of the next volume of People’s Education Edition
图5. 人教版八年级下册第十九章
4.2. 思维逻辑
思维逻辑回答的是“怎么教”与“怎么学”的问题,其指的是教师教与学生学活动中的思维规律。
依旧以高中数学人教A版必修一中第三章函数的概念与性质为例,教材中对于第三章第二节函数性质的教学先讲的是函数单调性,再是奇偶性,其实这种安排对于研究函数性质的逻辑关系是有问题的。对于研究问题的一般思维:首先我们从函数的整体性着手,看其是否有对称性。这也符合大多数人的认知规律,比如拿到一个函数图像,首先看到的是图像的整体布局,接着注意到的才是细节。如果研究的函数具有对称性,观察函数图像的对称属性,接着对其一半进行单调性研究,这样有效地压缩了研究过程。还有人教版九年级上册二十一章第二节解一元二次方程,教材对其解法的安排顺序:1) 配方法;2) 公式法;3) 因式分解法,此安排是不符合思维逻辑的。这三种方法的设置均是用来解一元二次方程,不管是解一元二次方程还是解决其他问题,首先想到的应该是花费成本最低最有效的方法。然而因式分解法,是针对一些特殊的一元二次方程,求解起来更简单。因此拿到一个一元二次方程,首先观察方程是否满足因式分解易于察觉的求解形式,若满足便可轻松解答,若不能使用,便使用其他方法。第二小节选择配方法:1) 配方法没有涉及新的并且复杂的知识点,主要是移项,转化成完全平方形式,再求平方根,应用知识迁移很容易做到。2) 公式法的推导要借助配方法的推导,先编排配方法为后续公式法做铺垫。第三小节选择公式法:公式法具有一般性,观察一元二次方程没有任何特殊性,直接套用公式进行计算。所以对于一个有责任心的数学老师来说,我们要切实承担起提高学生数学思维能力的责任,在充满思维逻辑的课堂中,用鲜明的数学观点分析问题,让学生用充满数学逻辑的思维方法解决数学问题。
华罗庚在《和青年谈学习》中提出:“什么叫学深学透?这就是要经过‘由薄到厚’、‘由厚到薄’的过程” [7]。用这段话来分析理解数学教育,就是首先要打下坚实的基础,进行解题分析和知识理解,把教材读到“厚”。然后在自己独立思考之后,经过消化吸收,掌握其中的数学思想方法,就是“从厚到薄”的过程。除此之外,张奠宙先生认为中国数学教学是以模块的方式呈现(图6) [8]。米山国藏也曾说过:“学生在初、高中接受的数学知识,出校门不到一两年,很快就忘记,惟有深深铭刻于头脑中的数学精神,数学思维方法等随时随地发挥作用,使他们受益终身” [9]。由此可以看出学科知识是基础,是一切后续工作的前提,而思维方法将知识变得立体,并使其系统化,真正做到“从厚到薄”,让人受益终生。
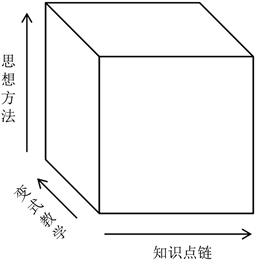
Figure 6. Middle school mathematics teaching module diagram
图6. 中学数学教学模块图
因此,对于教师来说,要学会准确把握数学学科逻辑和思维逻辑。在教学活动中揭示数学学科的本质,感受数学的教育价值,让学生在数学学习的过程中,体会教学逻辑的“美”。更重要的是让学生掌握研究数学问题的科学方法,养成理性的思维习惯,为他们以后的学习和研究做好准备。
基金项目
新疆维吾尔自治区高校科研计划自然科学重点项目(XJEDU2020I018)。
NOTES
*通讯作者。