1. 引言
嵌段共聚物是由两段或多段不同的子链组成的分子，它是一类有着独特性质的软物质材料[1] [2] 。它能够在纳米的尺度上形成有序的周期结构，是最理想的展示分子自组装的体系。目前随着纳米技术发展，特别是有机–高分子光电池技术发展的要求在有限的空间能够调整自组装结构的尺寸[3] ，此外光电子器件中应用的共轭高分子的刚性很强，通过接枝柔性嵌段来改善自组装的性能[4] 。这一种嵌段共聚物即为刚–柔二嵌段共聚物(rod-coil diblock copolymer)。在过去的十年中，相比柔性嵌段共聚物的自组装研究而言，针对刚–柔嵌段共聚模型的理论研究还十分不足。这严重制约了实验上合成和制备刚–柔嵌段共聚物体系自组装结构的发展[5] 。需要指出的是由于刚性嵌段的引入，使得局域的相互作用变得非常复杂，此时相互作用的力程变得不可忽略[6] 。
本工作引入非硬壳排除体积相互作用势，讨论了相互作用力程以及相互作用强度对于刚–柔二嵌段共聚物有序–无序转变点的影响。
2. 模型与方法
我们考虑整个系统体积为V，其中共有n条刚–柔二嵌段共聚物高分子链。每条链总的链段的个数为N，其中柔性链段数为NC，刚性链段数为NR。定义刚性链段的体积分数为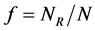
。整个体系的配分函数可以写为，
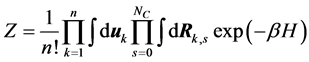
其哈密顿量为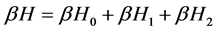
。
其中，
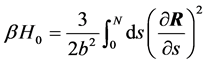
其中β = 1/kBT，kB为玻尔兹曼常数，T为温度，b为链库恩长度，s为沿链方向的周线变量，u为刚性嵌段的取向，R为柔性链段的构象，
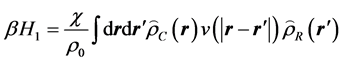
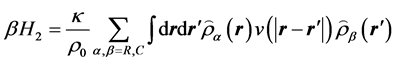
这里χ为Flory-Huggins相互作用参数，κ为Helfand压缩系数，当κ趋于无穷大，体系变为不可压缩流体；上面两式中刚性和柔性链段的密度算符可以定义为，
，
。
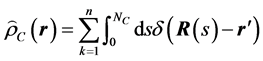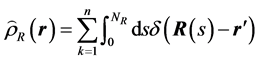需要特别指出的是本工作中采用了有限力程的相互作用势，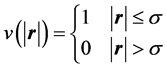
为相互作用力程。
通过引入单位元
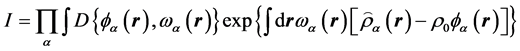
配分函数可以写为场的泛函形式
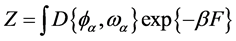
其中平均场的自由能表达式为
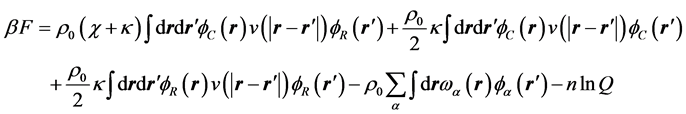
这里，单链配分函数为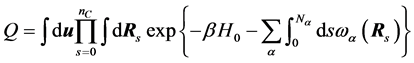
。
引入平均场近似
，可以求解体系可能处在的结构。均匀的无序相
，
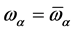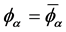总是平均场方程的一个解。为了考察均匀无序相的稳定性，即判定体系的spinodal线，我们考虑均相解附近的涨落
这样单链配分函数可以展开为
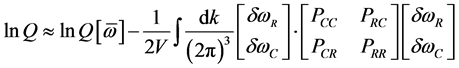
其中链内关联函数为，
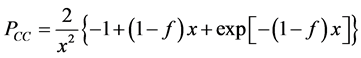
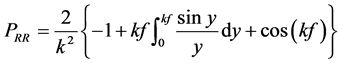
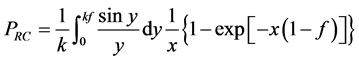
这里的
。带入到平均场的自由能表达式中可得
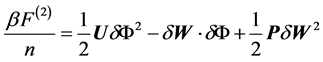
我们引入了相互作用的矩阵表达形式
，
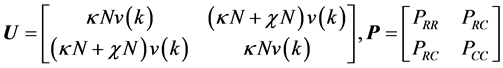和场的矢量的表达式
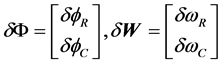
其中
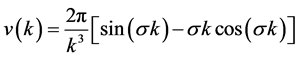
为具有有限力程相互作用在傅里叶空间中的表达式。引入无规相近似(Random phase approximation)
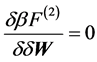
将外场δW积分掉，此时自由能仅为密度场的泛函，即我们得到了Landau形式的自由能
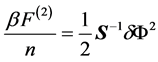
体系的不稳定线或spinodal线由如下公式确定，
，
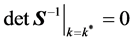k*为均相无序体系的最不稳定模式，1/k*为spinodal相分离后形成的有序相的特征宽度。本工作中，我们数值求解这一方程，来获得刚–柔二嵌段共聚物均匀无序相的spinodal线。
3. 结果与讨论
刚–柔二嵌段共聚物的自组装结构取决于两个嵌段的尺度。对于刚性嵌段，其链的构象行为是分形维为1的直线型构象，即R~N1。而对于柔性嵌段而言，其构象为分形维为1/2的无规行走构象，R~N1/2。这使得问题变得非常复杂，为了简化问题，我们关注当f = 0.5时的情况，也就是刚性嵌段和柔性嵌段都具有相同的链段数的情况。此时体系的无序、有序转变点受到相互势的强度大小影响。要特别指出的问题是在平均场理论的层面上对于柔性–柔性二嵌段共聚物f = 0.5对应于一个临界点，即spinodal线和binodal线在这一点上重合。而对于刚–柔二嵌段共聚物，并不存在临界点。
图1给出了无序、有序转变点随着链聚合度N的变化规律。从图中可以看出在给定压缩系数的情况下，随着链长的增加χN单调增加。当N > 10后对N的依赖变得不敏感，进一步，当N趋于无穷大，χN趋于某一固定值。当压缩系数增加，无序、有序转变点同样随之增加。当压缩系数趋于无穷大，无序、有序转变点趋于恒定值，如图1中所示κ = 1000与κ = 10,000，两条曲线几乎重合，此时体系变为不可压缩的刚–柔二嵌段共聚物的极限情况。此外也可以看出压缩系数对于无序、有序转变点的影响并不大，因为图中κ的取值变化为4个数量级，而χN的变化不到10%。
进一步我们研究了有序、无序转变点受刚性链段的长度的影响。事实上在给定聚合度的情况下体系的尺度受相互作用力程和刚性链段长度两个长度尺度的影响。这里我们以L/σ作为参数研究有序、无序转变点受相互作用力程的影响。这一考虑在传统的高分子场论模型中是被忽略掉的。这是由于，传统场论中关心柔性–柔性嵌段共聚物，在柔性高分子材料中，唯一重要的长度尺度为高分子链的回转半径Rg，这是一个介观尺度。而在微观尺度上的相互作用的力程在此时变得无关紧要。而当考虑刚–柔两性嵌段共聚物时，刚性–刚性、柔性–刚性嵌段间的相互作用时相互作用的力程不可忽略。
图2给出了刚–柔二嵌段共聚物无序、有序转变点受相互作用力程的影响。我们发现随着相互作用力程的增加，转变点持续升高，而且，这影响远远高于相互作用强度的影响。作用力程的变长，是相分离变得更加困难，体系更倾向于处在均匀的无序状态。事实上随着相互作用力程的变大，体系的相行为更趋向于小分子的行为，也就是高分子的链状特征逐渐变得不重要。这从不同L/σ的曲线中可以看出，随着L/σ的变大χN对N的依赖逐渐变得扁平，即逐渐对链长N变得不敏感。
4. 结论
本工作首次讨论软相互作用势对刚–柔二嵌段共聚物微观相分离的影响。采用具有有限力程的相互
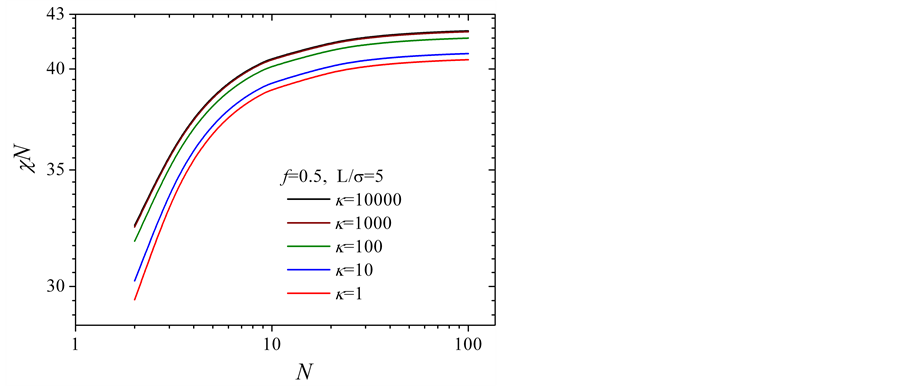
Figure 1. For f = 0.5, ODT depending on N and interaction parameter
图1. f = 0.5时，无序、有序转变点随链聚合度以及相互作用参数的变化
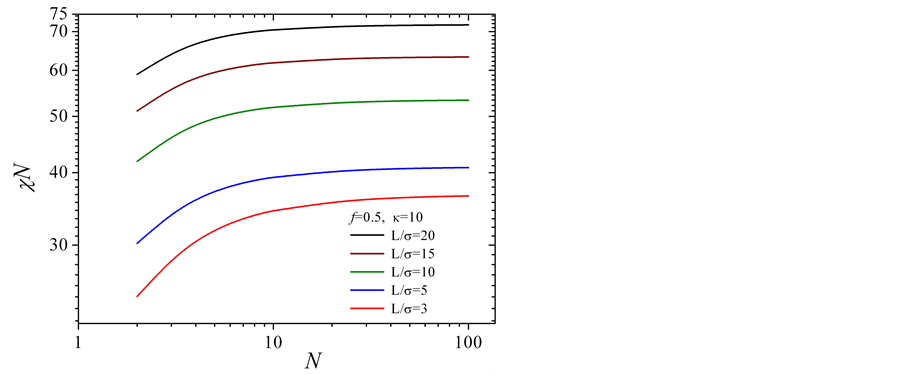
Figure 2. For f = 0.5, ODT depending on N and interaction range
图2. f = 0.5时，无序、有序转变点随链聚合度以及相互作用力程的变化
作用形式，并相互作用参数描述相互作用的强弱。这里的理论的推导，给出了刚–柔二嵌段共聚物的更加一般的理论工具。当压缩系数κ趋于无穷大时我们的理论回到经典的结果。数值计算表明，压缩系数和相互作用力程的增加有助于均相无序体系变得更稳定。
基金项目
中央高校基本科研业务费(2013JBM087)。