1. 引言
欧盟将航空运输业纳入EU ETS(欧盟排放交易体系)这一举措，给世界航空运输业的发展带来了更多不确定性，航空运输业节能减排成了世界各国都必须面对的议题。欧盟规定2012年开始，所有从欧盟成员国起飞或在欧盟成员国落地的航班都将纳入到碳排放交易体系中，这将直接关系到我国运营中欧航线航空公司的经济利益。不少学者认为，欧盟将航空业纳入排放交易系统对我国航空业造成的影响是不可估量的，我国只有积极应对，才能化解危机。比如建立中国的航空业碳排放交易体系，采取相应的减排措施，通过与欧盟谈判，争取互相豁免双方的碳排放收费。中国在应对气候变化领域是主力军，已经制定了包括航空业在内的国内减排目标与减排相关扶助政策法规；但我国作为全球减排潜力最大的国家，也是减排压力最大的国家，无论是从为了促进实现国内节能减排目标，还是从降低成本以获取参与制定规则和定价的权力以维护国家利益的角度，建立我国的航空运输业碳排放交易体系都是必要的[1] 。
本文就是以此背景假设出发，假设我国建立航空运输业碳排放交易体系后，建立基于企业行为理论的航空运输业成本转嫁实证模型，试图分析不同类型航空公司的成本转嫁能力，并对行业内成本转嫁问题做出总体性的估计。需要指出的是，模型的结果可以对航空运输业成本转嫁能力问题给出指导性的意见，却不可能是准确的预测，因为现实情景远比模型更加复杂和微妙。
本研究意欲抛砖引玉，有两点研究意义。一为航空公司决策者解答“碳排放成本会对航空公司造成怎样影响？”问题。各个航空公司的市场需求、消费者构成以及航线类型不尽相同，碳排放成本将给不同公司造成不同影响。从本文研究结果来看，休闲航线市场和商务航线市场的成本转嫁率分散在50%~ 283%之间。航空公司需结合自身特点，才能妥善应对航空公司碳排放成本所带来的机遇和挑战，适当调整市场战略，取得节能减排和保证企业利润的双赢局面。二为政策制定者解答“碳排放成本会对航空运输业造成怎样影响？”这一问题。文章得出行业总成本转嫁率接近100%的结论，与欧盟委员会的影响评估报告和许多研究结果不谋而合。考虑到100%的行业成本转嫁率正是欧盟建立EU ETS的根据之一，建立我国的碳排放交易体系，也需要类似的学术研究成果作为理论支持。
2. 建模方法
本模型参考了Hepburn、Quah和Ritz[2] 以及Defra and DfT[3] 的研究成果，相比较其他成本转嫁理论模型的优势在于：
1) 考虑了需求函数的曲率，而非将需求函数单一假设为线性需求函数；
2) 考虑了航空运输业本身的特点，将航空公司采用的不同市场战略——利润最大化(航空公司合理利用收益管理)、销售额最大化(航空公司以提高客座率为目标)和市场份额最大化(航空公司努力提高市场占有率)——考虑到模型内。
2.1. 模型的假设
本模型的关键假设如下：
1) 单一厂商多生产一单位商品的成本与总产量无关。单一厂商的单位成本(固定成本)与市场内其他厂商的单位成本(固定成本)无关。在航空运输业中，这该假设富有说服力，因为一定范围内，航空公司多运输一位旅客的成本很小，与该航班的总成本无关；
2) 厂商以利润最大化、销售额最大化或市场份额最大化作为其市场战略；
3) 厂商不采取减少污染的措施；
4) 厂商不面临排放交易系统外厂商的竞争；
5) 假设厂商拥有线性成本函数，即边际成本不变；
6) 不存在市场进入和退出。
2.2. 航空运输业成本转嫁模型
本模型衍生自古诺模型。古诺模型假设厂商间进行产量竞争而不是价格竞争。产量竞争这一假设一直备受争议，因为现实中厂商更多进行的是价格竞争。但也有不少学者肯定古诺模型假设的有效性，如Kreps[4] 认为如果厂商在决定产量后进行价格竞争，则古诺模型依然有效。航空公司往往先进行新航线确定和新飞机购买、租赁这些中期决策，并根据短期市场变化做出票价调整。航空运输业的行业特点正符合Kreps的论断。
推导利润最大化、销售额最大化或市场份额最大化三种市场策略下，航空公司成本转嫁率公式。
2.2.1. 利润最大化
根据Defra and DfT[3] 的基本模型，当厂商以利润最大化作为市场战略时，均衡点的边际收益等于边际成本，当边际成本增加时，厂商会相应提高其边际收益。成本转嫁率可表示为：
其中
为厂商数量，
为需求曲率参数，
，
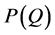为反需求函数。
该成本转嫁公式与厂商的市场份额分布无关，即对同等规模厂商竞争或非同等规模竞争同样适用。公式本身可得出几个直观的结论：
1) 成本转嫁率随需求曲率E的增加而增加，并因为
，
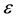为需求价格弹性，成本转嫁率随需求价格弹性的增加而减小；
2) 特别的，当需求函数为log-liner形式时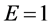
，则无论市场中有多少竞争厂商，成本转嫁率都为100%；如果需求函数为凸，
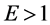。比如在常需求价格弹性下，无论市场中有多少竞争厂商，成本转嫁率都超过100%；如果需求函数为凹，
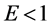，比如在线性需求
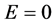时，无论市场中有多少竞争厂商，成本转嫁率都小于100%；
3) 当厂商数量无限大，市场结构接近完全竞争时，成本转嫁率接近100%。
2.2.2. 销售额最大化
Ritz[5] 研究了销售收入最大化市场战略下的成本转嫁问题，此时成本转嫁率公式为：
该公式假设市场中竞争厂商规模相同，每个厂商的市场份额为
。和厂商采用利润最大化市场策略类似，若厂商采取销售额最大化策略，当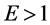
(
，
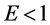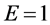)时，成本转嫁率大于(小于，等于)100%，与厂商数量无关，当厂商数量越来越大，市场结构趋于完全竞争时，成本转嫁率趋于100%。
销售额最大化市场战略下成本转嫁的一个特殊之处在于，成本转嫁率存在下限，无论何种类型的需求函数，成本转嫁率都高于50%。并且同一厂商在销售额最大化市场战略下的成本转嫁率，比该厂商采取利润最大化市场战略下更接近100%。这种现象的解释之一为，在销售额最大化市场战略下，厂商的表现更接近市场中存在大量竞争者，因而将成本转嫁率推向完全竞争时的100%。
2.2.3. 市场份额最大化
根据Defra and DfT[3] 的模型，市场份额最大化市场战略下的成本转嫁与销售额最大化市场战略下成本转嫁相似，但是公式更复杂：
其中
满足方程：
该公式也假设市场中竞争厂商规模相同，每个厂商的市场份额为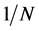
。当
(
，
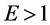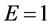)时，成本转嫁率大于(小于，等于)100%，与厂商数量无关，当厂商数量越来越大，市场结构趋于完全竞争时，成本转嫁率趋于100%。此时成本转嫁率的下限大约为33%，且与需求函数形式无关，其他直观结论与销售额最大化市场策略下相同。
2.3. 参数的获得
根据航空运输业本身的特点，模型输入了特定参数E，即需求曲率，以反应消费者对票价变化的回应程度。E代表的是需求曲线斜率的弹性，即斜率变化带来的总量变化。常见的需求函数的需求曲率大多为常数，比如线性需求函数、log-linear需求函数以及常弹性需求函数。图1直观给出了几种常见需求函数的曲率，线性需求函数的需求曲率E为0，凹需求函数的需求曲率E为负，凸需求函数的需求曲率E为正值。
Hepburn、Quah和Ritz[2] 研究了需求函数上某点需求曲率E与需求价格弹性的关系：
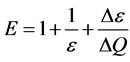，其中
根据上述公式，我们可以通过需求价格弹性得出需求曲率E。但我国航空运输市场需求函数及需求价格弹性数据皆少有研究涉足，本文通过另一种途径，借鉴Defra and DfT[3] 对欧洲航空运输市场需求价格弹性的估计方法，参考其数据估计我国局部航线市场需求价格弹性数据。Defra and DfT将市场划分为休闲类、商务类和低成本类，并考虑三类市场中长程和短程航线的不同，具体如下：
2.3.1. 休闲类(Leisure)
Defra and DfT总结相关研究，发现短程休闲局部航线市场的价格弹性约为1.4~1.5，见表1和表2，高于CE Delft[6] 收集汇总的数据结果。根据Brons[7] 的研究，旅客的价格敏感性以1%的速率逐年降低，
Figure 1. Demand curves and the demand curvature parameter E
图1. 需求曲线与需求曲率E的关系
Table 1. Review studies of price elasticities of demand
表1. 需求价格弹性研究结果总结表
来源：Defra and DfT。
Table 2. Further studies reporting price elasticities of demand
表2. 更多需求价格弹性研究结果总结
来源：Defra and DfT. Note：SR = 短程，LR = 长程。
Defra and DfT最终将数据范围选定在0.7~1.3之间。
2.3.2. 商务类(Business)
Brons[7] 认为商务旅客的价格弹性比休闲旅客低0.55，原因在于飞行对商务旅客的价值远高于对休闲旅客的价值。如果票价升高，商务旅客不会像休闲旅客那样大幅减少飞行频率。并且商务旅客往往选择特定机场和特定时间段，其飞行时间段与飞行目的地更具局限性。Defra and DfT将弹性范围定为0.3~0.7，数据来源为CAA[8] 、Jorge-Calderon[9] 和Dargay-Hanley[10] 。
2.3.3. 低成本类(Low-Fare)
针对低成本类需求价格弹性的研究相对较少。Battersby and Oczkowski[11] 对四条澳大利亚国内航线的低成本航空需求价格弹性进行估计，结果为0.59，低于经济舱的1.68和商务舱的0.58。CAA[8] 也指出低成本航空的需求价格弹性较低。但是也有研究认为低成本航空的需求弹性可能高于1，如PricewaterhouseCoopers[12] 。
2.3.4. 长程航线与短程航线
长程航线票价较高，可能具有更高的价格弹性。Jorge-Calderon[9] 发现欧盟境内航班比境外航班的价格弹性更高。然而，旅客在远距离运输时缺乏其他替代运输方式，这会降低长程航线的价格弹性。如Brons[7] 的研究表明航程与价格弹性的关系很小。
综上，我们不对长程航线与短程航线的需求价格弹性做出区分。并根据Defra and DfT的研究结果，结合我国航线市场的情况，表3列出了本研究对需求价格弹性的估计范围，以计算需求曲率E。
2.4. 数据的选取
本文选取具我国有代表性的局部航线市场作为数据样本来源。
首先参考欧盟委员会对局部航线市场定义的专家意见，对局部航线市场进行定义。欧盟将旅客分为时间敏感旅客和非时间敏感旅客，并用旅行目的代表作为时间敏感度的区分标准，将其用商务旅客和休闲旅客表示。在地域上，用城市对划分市场边界，并且对于时间敏感旅客更倾向于将边界具体到机场–机场。比如伦敦希斯罗机场–马德里的商务市场应与伦敦卢顿机场–马德里的商务市场相区别。但如果考虑休闲市场，则只有伦敦–马德里一个。城市对界定的局部航线市场，可包含直飞航班和中转航班。直飞航班为确定一个起飞点，然后在中途不许停留，直达指定的降落点，不改变航线，不中途降落；中转航班指航空公司将航班资源进行有效的组合，形成航线网络，将旅客从始发地经一个或多个中转地运送至目的地。所以在实际应用时，某个航线市场，尤其是长距离航线市场，通常包含着多个竞争机场和中转航班。
本研究选取了我国8个具有代表性的局部航线市场，航班时刻数据源自信天游(travelsky)网站公布的2013年度秋季航班时刻安排(不考虑航空公司间控股关系)，见表4。
值得注意的是，本研究更关注局部航线市场上宏观竞争航空公司的数量。实际上，航班时刻和航班频率也影响竞争程度，本模型并未考量其中，特此指出，以求完善。
3. 模型结果
将我国典型城市对局部航线市场数据以及需求弹性数据代入模型进行运算。模拟结果见表5和表6 (注阴影部分内的需求函数估计形式较不适用于其对应的航线类型，仅做参考)
4. 模拟结果解释
线性需求下的成本转嫁率范围在50%~94%之间，在利润最大化市场战略少数航空公司竞争时最低。线性需求函数较常弹性需求函数更符合休闲局部航线市场的特征，本研究选取了北京–丽江、上海–景洪、
Table 3. Ranges of price elasticities of demand chosen by this paper
表3. 本研究的需求价格弹性估计范围
Table 4. The number of airlines serving city pairs
表4. 城市对局部航线市场中的竞争者数量
Table 5. Cost pass-through in leisure routes under different firm strategies
表5. 休闲航线成本转嫁率模拟结果
注：阴影部分内的估计需求函数较不适用于休闲航线，仅做参考。
Table 6. Cost pass-through in business routes under different firm strategies
表6. 商务航线成本转嫁率模拟结果
注：阴影部分内的估计需求函数较不适用于商务航线，仅做参考。
北京–黄山和上海–拉萨四个典型的局部航线市场为代表，其结果呈现在表5中。
常弹性需求下的成本转嫁率范围在102%~283%之间。常弹性需求函数较线性需求函数更符合商务局部航线市场的特征。本研究选取了北京–上海、北京–深圳、北京–广州和上海–郑州四个典型的局部航线市场为代表，其结果呈现在表6中。
观察两组模拟结果可以发现，当航空公司采取销售额最大化市场战略时，成本转嫁率更接近100%，而采取利润最大化市场战略时，成本转嫁率更偏离完全转嫁(更高或者更低)，而市场份额最大化市场战略的结果处于两者之间。低需求价格弹性，即旅客对票价变化不敏感时，成本转嫁率更高。
休闲航线市场需求为线性形式，即休闲旅客拥有更高的需求价格弹性，其成本转嫁率低于100%，尤其在只有一家航空公司提供运输服务的北京–黄山航线，转嫁率只有50%。但随着市场中竞争厂商数量的增加，转嫁率逐渐增大，趋于100%，如4家航空公司竞争的上海–拉萨航线市场，转嫁率最高能达到94%。
商务航线市场的常弹性需求意味着旅客对票价较不敏感，直观表现为航空公司可以转移出更多成本，与模拟结果一致。在只有4家航空公司竞争的上海–郑州市场上，成本转嫁率最高能达到151%~283%。而随着竞争的加剧，成本转嫁率同样趋于100%，如北京–上海市场，有10家航空公司提供服务，成本转嫁率最低仅为102%~103%。航空运输市场主要由商务和休闲两类市场组成，本研究认为，综合来看，我国航空运输市场的成本转嫁率应接近100%，和欧盟委员会的预测结果类似，和不少国外成本转嫁研究的实证结果不谋而合。
需要注意的是，本模拟结果建立在碳排放交易机制引入后，市场中竞争的航空公司数量并未改变的假设上。也即碳排放交易成本只占原有票价的较小部分，除少数低成本航空公司推出的特价票(如春秋航空的99元机票)外，本假设可以成立。
5. 分析与结论
结合休闲航线市场和商务航线市场的模拟结果，成本转嫁率的跨度竟达到了50%~283%，但若将整个市场看做一家航空公司，便可以形象地理解这一现象。如果该航空公司的客户群对价格十分敏感，譬如每提高一元票价都将失去固定数量的旅客(即航空公司面临线性需求函数)，则航空公司提升的票价必然小于碳排放成本，即成本转嫁率低于100%，因为较低的成本转嫁率可以确保更高的收益；相反，若这家航空所在市场的消费者对价格不敏感，比如任何价格下，提价1%只减少固定比例的需求，则将价格大幅提高后，需求减少带来的损失控制在可接受的范围内。如此一来，航空公司倾向于提价来弥补承担的碳排放成本，因为其具有垄断的市场力量和价格不敏感的消费者。真实的市场类型在上述两种极端例子之间摆动，并且市场的竞争性越强，成本转嫁率越接近100%。另当局部航线市场的需要由多样化旅客类型构成时，成本转嫁率更可能超过100%。这是因为收入和偏好的横截面数据范围更广了，于是对价格变化的反应更平滑，使对价格变化更可能成比例，并且仍然有旅客愿意购买提价后的高价票。
在取得局部航线市场中需求函数的准确估计前，想估计出准确的成本转嫁率是不可能的。但综合分析，本模型模拟了我国航空公司采用不同市场战略以及面对不同旅客类型时，不同类型航线市场的成本转嫁率，得出了行业成本转嫁率接近100%的结论，但不同局部航线市场的转嫁率有所区别。该结论与欧盟委员会的影响评估报告和许多研究结果类似。