1. 引言
随着我国经济的发展,单一化的运输模式已经无法满足市场的需要。多式联运以其时效性强、灵活性好、耗费时间短、价格适中等优势而被逐渐接受。研究多式联运的路径选择问题,对于减少物流成本和缩短运输时间有着重要的意义。
近年来,围绕多式联运运输方案和路径的选择,已有许多相关的研究,并取得了一定的成果。谢芳等利用AHP层次分析法,将影响多式联运路径选择的因素进行排序,基于此排序选出有利方案[1] ;卢欣等利用K最短路法的求解思路,解出时间、费用的最短路,进而得到多式联运方案的最优解[2] ;鲁守备等采用区间权重法,通过对方案影响因素进行权重比较,得出优势方案[3] ;李蕾利用模糊综合评判和层次分析法对郑州至鹿特丹多式联运路径选择进行了分析[4] ;杨菊花等以应急物资运输过程中成本最小且运量最大为目标,构建多式联运运输网络,并利用Dijkstra算法对算例进行了求解[5] 。以往研究中,传统的层次分析法、区间权重法、模糊评价法等评价手段对指标权重的计算过程复杂,容易出错,特别是在指标繁多的情况下,结果容易出现偏差,整体实用性不强。
本文采用了一种基于专家偏好度的可拓层次分析法,该方法在专家打分的基础上,利用关联函数,得到可拓数值判断矩阵。同时结合传统AHP的方法,对各个方案进行排序,得出优选方案。
2. 影响多式联运路径选择的因素
2.1. 因素的选择
本文参考以往的研究成果,主要考虑了影响多式联运路径选择的几个突出因素。运输方式的经济和技术是决定多式联运路径选择的主要因素。从技术角度来看,速度快是物流运输服务的基本要求。但相对的,用较短的时间完成运输的全过程,势必造成运输费用的上升。从经济的角度看,要降低运输的费用,就意味着降低物流过程中服务的水平,或者选择有价格优势但速度较低的运输方式。而现实中,不同运输方式的相同运输属性总是不同,如何平衡运输过程中经济和技术的影响,是路径选择的一个关键问题。
近年来,随着多式联运所选路径沿路区域的快速发展,多式联运对社会效益的影响越发显著,因此,在选择多式联运的路径时,也需要对路径周边区域的就业机会、周边资源利用的程度、沿路周围环境的影响、文物古迹自然风光的保护等因素加以考虑。
2.2. 影响多式联运路径选择的因素
1) 经济因素。如何在限定的时间内,经济、快速、安全的将货物从出发地运到目的地,是路径选择过程中面对的主要问题。这其中,经济因素是决定物流成本的关键因素,不论对货主还是对物流企业都是运输合理化的一个重要标志。经济因素包括运输费用和路径费用以及其它物流过程产生的费用。运输费用即选择不同的运输方式所产生的运费;路径成本即选择不同线路时相应的运费;除此之外还包括装卸费用、运输过程中等待的费用、以及仓储的费用,本文中将这些费用归为其它费用。
2) 技术因素。主要包括运输时间、运输质量、运输线路的服务水平等。在全部物流活动所耗费的时间中,运输时间占去了很大的一部分。运输时间的长短决定着整个物流过程的花费时间。对于多式联运的经营人,运输时间不仅包括各区段的运输时间,还包括中转时间和必要的仓储时间。运输质量主要是指没有货损和货物灭失。运输质量高的路线可以减少货物收到自然灾害或者不可抗力造成的损失。线路的服务水平主要包括口岸设施条件、手续办理的便携程度、运输信息的畅通和港口及场站的服务质量等等。服务水平高的线路可以减少工作的层次,提高工作的效率,缩短在口岸或者场站的等待时间。
3) 社会效益因素。包括对资源的利用程度、对沿路周围环境的影响、对网络规划的影响、对增加就业机会的影响等。选择合适的运输线路,意味着对既有设施和路段的充分利用,同时不破坏沿路的自然资源、历史遗迹等。综合运输系统可以通过多式联运实现优化,以提高效率、促进发展、保证安全的前提下,以最小的花费提供优质的服务(图1)。
3. 基于专家偏好度的可拓层次分析法
3.1. 基本思想
可拓层次分析法在计算可拓判断矩阵以及确定权重的过程中,工作量大,过程复杂。因而,针对可拓判断矩阵单值化的研究是有必要的。基于专家偏好度的可拓层次分析法,以可拓层次分析法为基础,
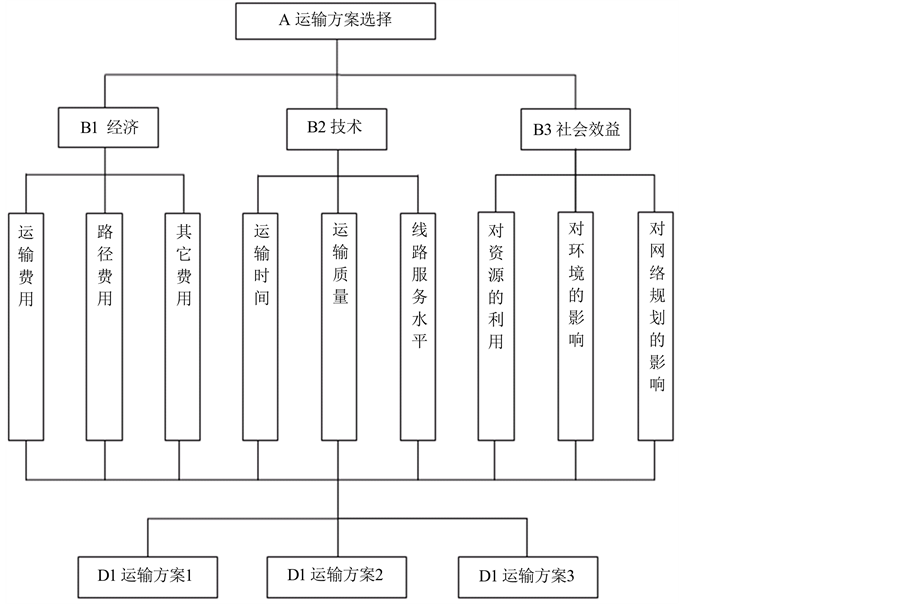
Figure 1. Hierarchy model of multimodal transport scheme evaluation
图1. 多式联运方案评价指标递阶层次结构图
将判断矩阵转化为单纯的数值矩阵,然后对该数值矩阵进行一致性检验。若该数值矩阵一致性良好,就采用经典层次分析法(AHP)求特征向量,最终得到权重;若数值矩阵一致性不好,则直接采用改进的层次分析法来求解数值矩阵,最后得到权重。
3.2. 构造可拓判断矩阵
论文依据互反型1-9标度法,以专家对各个影响指标的打分为依据,建立可拓判断矩阵,该矩阵反应了各个影响因素间的相对重要性。在EAHP中,用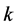 代表层次分析中的某一层,并将其与
代表层次分析中的某一层,并将其与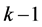 层相对应元素互相比较,最后采用可拓区间数来定量表示相对重要程度,以可拓区间数构成判断矩阵
层相对应元素互相比较,最后采用可拓区间数来定量表示相对重要程度,以可拓区间数构成判断矩阵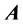 。其中
。其中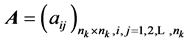 为互反矩阵,即:
为互反矩阵,即:
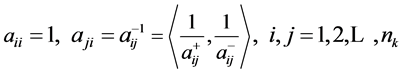 (1)
(1)
式(1)中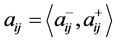 是一个可拓区间数,
是一个可拓区间数,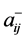 ,
,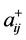 分别表示由可拓区间数构成的判断矩阵中第
分别表示由可拓区间数构成的判断矩阵中第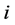 行第
行第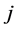 列元素的上下端点。其中,可拓区间数的中值
列元素的上下端点。其中,可拓区间数的中值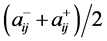 就是层次分析法中判断相对重要性时所采用的1-9标度中的整数[6] 。
就是层次分析法中判断相对重要性时所采用的1-9标度中的整数[6] 。
3.3. 可拓判断矩阵数值化
以往的研究中,可拓区间数判断矩阵的单值化往往采用区间数的中值。但是取区间中点值作为元素的相对权重无法保证准确性,各个元素的真实权重值也许偏离区间数中值,从而产生误差。本文从简化EAPH的计算过程的考虑出发,采用可拓区间数的关联函数,对判断矩阵进行单值化处理。
设可拓区间数矩阵为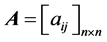 ,可拓区间数矩阵的数值化可由以下公式实现:
,可拓区间数矩阵的数值化可由以下公式实现:
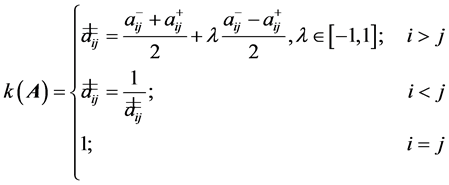 (2)
(2)
其中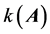 为关联函数,通过关联函数将可拓区间数矩阵
为关联函数,通过关联函数将可拓区间数矩阵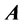 转化为数值矩阵
转化为数值矩阵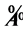 ,
,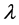 代表专家偏好度。
代表专家偏好度。
3.4. 一致性检验
可拓层次分析法需通过计算权重向量,来检验可拓区间数矩阵的一致性。本文采用的基于专家偏好度的可拓层次分析法的一致性检验相对简单,具体的检验方法可以通过以下两条定理实现:
1) 当且仅当下列不等式成立时,可拓区间数判断矩阵具有一致性:
 (3)
(3)
2) 设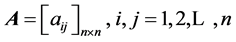 为可拓区间数判断矩阵,存在数值判断矩阵
为可拓区间数判断矩阵,存在数值判断矩阵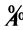 ,其中
,其中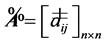 且
且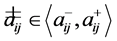 满足一致性的充要条件是对任意的
满足一致性的充要条件是对任意的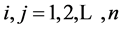 均有
均有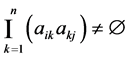 成立[7] 。
成立[7] 。
根据上述两条定理,可知,区间数矩阵范围内存在可以达到满意一致性的矩阵。通过这种方法检验其一致性,对比传统的层次分析法,大大减少了工作量。
4. 计算实例
1) 综合各个专家的意见对各个影响因素打分,得出区间打分表。下文先以目标层的计算为例,首先请专家对影响路径选择的几个主要因素进行打分,对几个专家的打分进行综合比较,得到打分的区间数(表1)。
2) 将区间分布表转换为数值判断矩阵。由上表得:
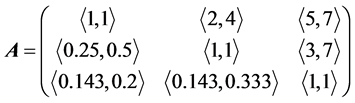
3) 利用一致性检验的公式来检验可拓矩阵的一致性;目标层的一致性检验如下,对区间取交集,若交集不为空则说明一致性良好:
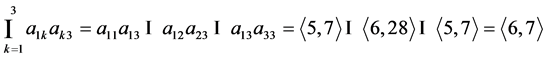 ;
;
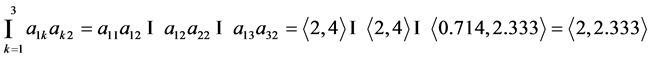 ;
;
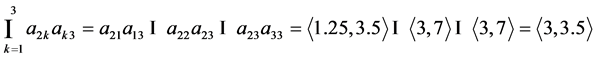 。
。
4) 如果计算结果通过了一致性检验,则利用关联函数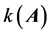 ,将结果转化为数值矩阵。取专家偏好度为
,将结果转化为数值矩阵。取专家偏好度为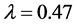 ,利用可拓区间数值化函数,得数值矩阵:
,利用可拓区间数值化函数,得数值矩阵:
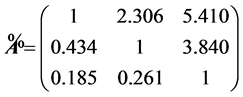
5) 对简化后的数值矩阵进行一致性检验,若通过一致性检验,则用层次分析法,求出权重,进行排序计算。对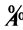 进行一致性检验,由于
进行一致性检验,由于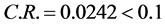 ,则满足一致性检验。权重矩阵
,则满足一致性检验。权重矩阵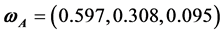 。
。
6) 对准则层、决策层重复以上步骤。最后对权重进行总排序,分析出关键因素。
最后三种方案归一化的结果有: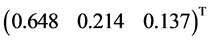 。方案3得分最高,比起其他方案优越性更好。同时通过检验可以发现,基于专家度的EAHP法和普通的AHP法比起来,结果相似,但是计算过程被大大缩短,对于简化计算有着重要的意义。
。方案3得分最高,比起其他方案优越性更好。同时通过检验可以发现,基于专家度的EAHP法和普通的AHP法比起来,结果相似,但是计算过程被大大缩短,对于简化计算有着重要的意义。
5. 结束语
多式联运方案的筛选方法对于缩短物流成本,减少物流时间有着重要的意义。本文在可拓层次分析法的基础上加以改进,利用基于专家偏好度的思想来简化计算,解决了选择方案过程中定性问题在定量化处理时遇到的主观判断模糊的情况,具有很强的可操作性和现实意义。

Table 1. Interval distribution factors of target layer
表1. 目标要素区间分布