1. 引言
在当今信息爆炸时代，数据已渗透到每一个行业和业务职能领域，成为重要的生产因素，引起了产业界、科技界和政府部门的高度关注，大数据挖掘技术已经上升为国家战略。分类、估计、检验、回归分析、相关性分析等构成数据挖掘的核心内容。多元统计分析是处理多维同体观测数据的数学方法，是数理统计学近几十年迅速发展的一个分支，计算机技术的发展为多元统计方法应用提供了便利的计算工具 [1] [2] [3] 。多元统计方法在工业、农业、医学、环境以及经济管理等诸多领域中有着十分广泛的应用。
主成分分析是多元统计的核心内容之一，广泛应用于多指标的综合评价体系，得到了科研工作者的一致认同，但在应用中存在这样或那样的问题，研究者从不同角度分析问题存在的原因并给出相应的解决办法。如林海明等 [4] 给出了主成分分析综合评价的应用条件；胡永宏 [5] 认为，第一主成分后面的主成分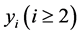
出现比较多的负数时，是否反向为
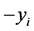没有公认的准则；阎慈琳 [6] 将主成分分析改进用因子分析综合评价，指出用主成分分析综合评价的问题之一在于同一特征值对应方向相反的特征向量，选取不同的特征向量组合对综合结果造成很大影响；叶双峰 [7] 认为采用标准化处理数据会造成信息的丢失，并从改进主成分分析的数据无量纲处理方法和采用非线性变换的主成分分析评价优化模型；孙刘平等 [8] 借用熵值法和主成分综合集成评价；徐静雅 [9] 指出通过综合评价函数计算得分不仅不能提高信息量(增加方差贡献率)，反而会减少方差贡献率；王学民 [10] 指出，不对主成分综合评价函数的实际含义加以解释，直接用这些指标对样品进行排序意义不大。符一平等 [11] 利用ARCH模型研究了上证综指的系列性质；王思哲等 [12] 利用方差分析对葡萄酒的评价进行了可信性研究，利用主成分分析和聚类分析方法对葡萄酒进行分级研究，并指出了葡萄酒理化指标与酿酒葡萄理化指标之间的相关关系。
本文收集2013年31个省市自治区部分高校有关人文社科科研方面的相关数据 [1] ，利用多种方法对各省市科研综合实力进行评价研究，并指出各种方法的优劣。收集的变量有投入科研活动的人年数、投入高级职称人年数、立项课题数、投入科研事业费、发表论文数、发表专著数、获得奖励数等。本文的主要结构是：针对主成分综合评价存在的问题，提出一些改进措施，给出了主成分综合评价的应用条件；以信息熵为工具，利用指标的变异程度度量信息差异，为科研综合实力评价提供方法依据；若第一主成分的评价结果与熵值法的评价结果通过Kendall协同系数检验，可以集成总的评价方案；通过对主成分得分进行k-均值聚类，并利用最终聚类中心为类间排序标准，第一主成分评分作为类内评价依据综合考量科研综合实力。SPSS20给出了各种方法的总评结果，并指出各种方法的优劣。
2. 主成分综合评价研究
主成分分析起源于20世纪初Karl Pearson和Charles Spearmen等人有关智力测验的统计分析中，广泛应用于多指标的综合评价体系。它的主要优点在于消除评价指标之间的相互影响，能更客观地描述变量的相对地位，同时，数学变换过程生成的信息量权数和系统权数比人为确定的权数更客观，操作性更强。本例中通过计算变量之间的简单相关系数和反映像相关矩阵(对角线上元素较接近1，其余元素的绝对值都较小)，适合进行因子分析，进一步，对数据进行巴特利特球度检验(Bartlett Test of Sphericity)和KMO (Kaiser Meyer Olkin)检验，表1给出了KMO值为0.846，变量间相关性较强，巴特利特球度检验统计量观测值为400.067，相应概率为0，小于给定的显著性水平(0.05)，变量适合进行因子分析。
根据原始变量的相关系数矩阵，采用主成分分析方法固定提取3个因子，为了对提取的因子有更好的解释，用方差最大法对因子载荷矩阵实施正交旋转，得到因子载荷矩阵。
林海明 [4] 指出，如果因子载荷矩阵每行载荷有绝对值靠近1，且列数较小，称因子载荷矩阵达到简单结构，并且前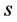
列主成分载荷矩阵达到简单结构，或者初始主成分载荷矩阵与旋转后的因子载荷矩阵都是差异不大的简单结构，则主成分有较为清楚的解释。表2的初始因子载荷矩阵(主成分矩阵)的第2列和第3列，旋转后因子载荷矩阵的第5列和第6列达到简单结构， 且第2列与第5列有差异不大的简单结构，主成分有较为清楚的解释；若显著性水平5%，显著相关的临界值
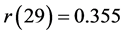，表2第二，三，四列的绝对值最大值分别为0.992、0.673和0.265，主成分
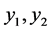与各指标显著相关，可以选取两个主成分
，累计方差贡献率达到94.886%。
主成分
与全部指标显著正相关，载荷都很大，且综合影响越大越好，
为正向的，可以解释为科研竞争力水平成分；主成分
与获奖数显著正相关(0.673)，与投入科研事业费(−0.313)和专著数(−0.277)负相关，获奖数是可以理解为前期科研成绩的累积，专著数理解为高水平科研人员前期长期工作成果的成果，
是正向的，可以解释为科研工作累积成分。相关系数矩阵的前两个特征值为
，将前两个主成分与各指标之间的关系(各指标标准化)表示为成分得分系数矩阵。
= 0.143投入人年数 + 0.181投入高级职称人年数 + 0.381投入科研事业费(百元) + 0.149课题总数 + 0.357专著数 + 0.027论文数 − 0.442获奖数
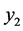= 0.080投入人年数 + 0.022投入高级职称人年数 − 0.332投入科研事业费(百元) + 0.063课题总数 − 0.283专著数 + 0.261论文数 + 0.946获奖数
构造主成分综合评价函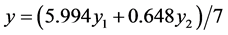
(7为特征值之和，权重系数按照方差贡献率确定)， 计算各省市科研综合实力得分并排序(见表5)。因子得分的均值为0，标准差为1，正值表示高于平均水平，负值表示低于平均水平。
需要指出的是，上述综合评价函数是当第一主成分方差贡献不够高(64.64%)时，采用以方差贡献率
Table 1. Test results of KMO and Bartlett in scientific research factor analysis
表1. 科研因子分析KMO和Bartlett的检验结果
为权重，构造的综合得分函数，这种方法看似能提高信息含量(提高方差贡献率)，其实是一种错觉 [2] 。事实上，设
分别为第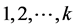
个主成分，综合得分函数
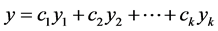的方差为
也就是说，综合得分的方差
小于第一主成分的方差
，第一主成分是所有原始变量线性组合(组合系数为单位向量)中方差最大者，通过综合得分不仅不能提高信息量(增加方差贡献率)，反而减少方差贡献率。因此，我们综合考虑第一第二主成分得分和排序效果会更好。
3. 熵值法评价方法研究
熵的概念产生于热力学，用来描述离子或分子运动的不可逆现象，后来引入到信息论中广泛应用于赋权，熵值法是一种客观赋权法，根据各项指标观测值所提供信息的大小来确定指标权重。设有
个变量，
个指标，形成原始指标数据矩阵
，对于某项指标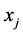
，指标值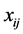
的差距越大，该项指标在综合评价中的作用越大，如果某项指标值全相等，则该项指标在综合评价中不起作用。在信息论中，熵是对不确定性的一种度量。信息量越大，不确定性就越小，熵值就越小，信息量越小，不确定性就越大，熵值越大。根据熵的特性，我们可以通过计算熵值来判断变量的随机性及无序程度，也可以用熵值来判断某个指标的离散程度，指标的离散程度越大，该指标对综合评价的影响越大。因此，可根据各项指标的变异程度，利用信息熵这个工具，计算出各个指标的权重，为多指标综合评价提供依据。熵值法是根据各项指标值的变异程度来确定指标权数的，这是一种客观赋权法，避免了人为因素带来的偏差，但由于忽略了指标本身重要程度，有时确定的指标权数会与预期的结果相差甚远，同时熵值法不能减少评价指标的维数。熵值法的基本步骤：
1) 将各指标同度量化，第
个指标下第
个变量比重为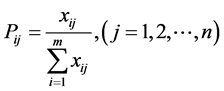
；
2) 计算第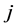
个指标的熵值：
，这里
，当某个指标的贡献趋于一致时，
趋于1，特别地，当指标值全相等时，可以不用考虑该指标在决策中的作用，即该指标的权重为0
3) 计算第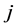
个指标的熵权：
，其中，
反应第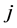
个指标下各变量贡献的一致性程度。
4) 计算综合评价值：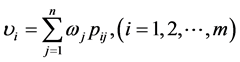
为第
个变量的综合评价值。
SPSS20计算出熵值法各省市评分和排名见表5。
4. 主成分熵值集成评价方法研究
利用信息熵为工具计算各指标的权重，为多指标评价提供依据，当所选指标过多就难免出现指标之间存在一定的关系，被评价对象的信息重叠性会造成被评价对象的歪曲评价；利用主成分筛选出的指标之间的相关关系较弱，能有效避免信息的重复性。如果采用第一主成分的评价结果与采用熵值法得到的综合评价结果通过协同系数一致性检验， 则可以考虑将两种方法的评价值进行集成综合评价。
Kendall协同系数检验是一种多配对样本的非参数检验方法，与Friedman检验相结合，实现对评价标准是否一致的判断。首先检验第一主成分评分和熵值法评分是否存在显著性差异，采用Friedman检验，然后将该问题延伸，不是从评分是否存在显著性差异的角度分析，而是在认定主成分评分和熵值法评分标准是否一致。如果利用Friedman方法检验出评分不存在显著性差异，则意味着两种方法的评价标准不一致。对评价标准的一致性检验可以通过Kendall协同系数检验来完成，其原假设是“主成分评价和熵值法评价标准不一致”。SPSS20自动计算协同系数统计量的观测值和对应概率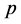
值，如果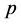
值小于给定的显著性水平(如0.05)，则拒绝原假设，认为两种方法评价标准一致；反之，如果
值大于给定的显著性水平，则接受原假设，认为两种方法评价标准不一致。
表3给出了第一主成分评价与熵值法评价的一致性检验，协同系数为0.051，在显著性水(0.05)下，认为两种方法具有一致性。我们可以将两种评价结果集成，权重系数可以通过专家根据经验确定(利用专家经验综合考量)，为了简单，选取综合评分函数为
。
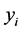为第一主成分评分，
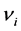为熵值法评分，表5给出了主成分熵值集成评价结果。
5. 主成分聚类评价方法研究
主成分熵值集成综合评价法能巧妙地综合主成分分析法和熵值法的优点，且通过了一致性检验，能有效评价省市科研综合实力。由于第一主成分方差贡献率不够高(64.64%)，第二主成分方差贡献率为30.24%，第一主成分包含原始数据的信息不够大，仅仅按照第一主成分得分排序有一定的片面性，可以考虑将主成分分析和聚类分析结合起来，采用主成分聚类评价。先将第一第二主成分得分标准化值(累计方差贡献率为94.886%)作k-均值聚类，分成4类，采用欧氏距离，最终类中心作为类间排序依据(本例类间排序顺序为1324) (表4)，类内按照第一主成分得分排序，得到省市综合评价结果(表5)。
Table 3. The results of Kendall synergy coefficient test
表3. Kendall 协同系数检验结果
Table 4. Principal component k-mean clustering final clustering center
表4. 主成分k-均值聚类最终聚类中心
Table 5. Evaluation of comprehensive strength of scientific research
表5. 各省市科研综合实力评价表
6. 结束语
主成分分析广泛应用于多指标的综合评价体系，得到了科研工作者的一致认同，但主成分综合评的局限性也是不可忽视的，一方面，主成分分析综合评价有一定的应用条件，如变量是正向的、标准化的，主成分载荷矩阵达到简单结构(或初始主成分的载荷矩阵与旋转后的因子载荷矩阵都是差异不大的简单结构)，主成分正向，主成分与变量显著相关等，缺乏应用条件会导致评价结果不合理甚至误判，另一方面，综合评价函数以方差贡献率为权重，不仅不能提高信息量(增加方差贡献率)，反而会减少方差贡献率。熵值法综合评价是以信息熵为工具，利用指标间的变异程度度量各指标的信息差异，为科研综合实力评价提供依据，但当指标之间存在相关关系时会导致被评价对象的信息具有一定的重复性，从而造成对被评价对象的歪曲评价。利用第一主成分与熵值法的综合评价结果，一方面，可以克服在第一主成分方差贡献率不能达到要求，选用多个主成分会导致综合评价函数权重系数不能确定的问题，另一方面，经过主成分筛选出来的指标之间的相关关系较弱，可以有效避免信息的重复，通过Kendall一致性检验能验证两种方法的一致性，因此，综合集成的结果较为理想， 但权重系数的确定也是一个值得商讨的问题。主成分聚类评价能有效避免第一主成分方差贡献率不足的问题，综合多个主成分能有效提高综合评价的信息量，一方面，类内评价采用第一主成分得分排序充分体现第一主成分的主导作用，也能有效避免系数权重的选取问题，另一方面，类间距离采用多个主成分欧氏距离计算同时会掩盖第一主成分的主导作用，当第一主成分方差贡献率比较大，第二主成分方差贡献率比较小时会导致歪曲的评价结果。在实际应用中，可以采用多种方法、考虑多种评价结果会达到更理想的效果。
基金项目
国家自然科学基金(项目编号11526065，11601108)、海南省自然科学基金(项目编号20161002)、海南大学教育教学改革研究项目(项目编号hdjy1715)和海南省中西部高校提升综合实力工作资金项目资助。
*通讯作者。