交流伺服系统自抗扰内模控制

ADRC and Internal Model Control for AC Servo System

摘要: 针对火箭炮伺服系统存在比较大的不确定性及外部干扰，本文提出了一种高精度自抗扰内模控制方法，即针对电流环采用内模控制器，克服传统内模控制对电机参数敏感的问题，而速度环采用自抗扰控制器，提高系统对外部负载扰动抑制能力，以期获得良好的跟踪性能及强鲁棒性。最后通过仿真验证系统具有强鲁棒性和良好的跟踪性能，证实了该方法的有效性。

Abstract: Aimed at fairly big uncertainty and outer disturbance existing in servo system of rocket launcher, a high precision ADRC-IMC is put forward. That is to say, IMC is adapted in current loop to overcome sensitivity to motor parameters encountered in traditional IMC. While, ADRC is adapted in speed loop in order to resist outer load disturbance to obtain good tracking performance and strong robustness. In the end, strong robustness and good tracking performance of the system are validated by simulation test.

1. 引言

某型号火箭炮伺服系统的特征参量，如谐振频率、阻尼、燃气流冲击以及负载干扰等，会随着带弹量、目标位置的变化以及工况变化的影响而相应产生相当大的变化，使得系统的不确定性非常大，让控制系统的设计者感到困难。

1982年，C. E. Garcia和M. Morari提出具有模型、控制、反馈环节的内模控制结构，其产生背景主要有两个方面：一是对当时的两种预测控制算法MAC和DMC进行系统分析；其次是作为Smith预估器的一种扩展，其设计更为简单，鲁棒性及抗干扰性大为改善。内模控制(Internal Model Control，简称IMC)是一种基于过程数学模型进行控制器设计的新型控制策略。IMC具有实用性强，结构简单，设计直观，不需要精确的对象模型，在线调节参数少，调整容易等优点。特别是对于鲁棒性及抗干扰性的改善和对大时滞系统的控制，效果尤为显著，而且也为非线性系统的控制提供了一条有效的途径。由于具有良好的跟踪性能和抗干扰能力，并对模型失配有一定的鲁棒性，使其在工业过程控制中获得了越来越广泛的应用。此外，内模控制还和许多其它控制方式相结合，如内模控制与模糊控制、内模控制和自适应控制、内模控制和最优控制、预测控制的结合使内模控制不断得到改进并广泛应用于工程实践中，取得了良好的效果。

本文通过对永磁同步电机转速特性的分析，采用自抗扰技术实现对电机速度的控制，该控制器由跟踪微分器(TD)、扩张状态观测器(ESO)、非线性状态误差反馈3部分组成 [1] 。该方法不依赖系统的具体数学模型，不区分系统的内部与外部扰动，而是直接观测并实时补偿系统的总扰动，使系统的鲁棒性强。

2. 电机数学模型

火箭炮伺服系统由PMSM、控制器、驱动器、传感器等组成，其目的是实现对给定位置的精确跟踪。假设定子为三相对称绕组，转子无阻尼绕组，气隙磁场呈正弦分布，磁路不饱和，不计磁滞和涡流损耗影响，PMSM的数学模型为：

$\{\begin{array}{l}\stackrel{\dot{}}{\omega }=\frac{3p{\psi }_f}{2J}{i}_q-\frac{B}{J}\omega -\frac{T_L}{J}\\ \frac{\text{d}{i}_q}{\text{d}t}=-\frac{R}{L}{i}_q-p\omega i_d-\frac{p{\psi }_f}{L}\omega +\frac{u_q}{L}\\ \frac{\text{d}{i}_d}{\text{d}t}=-\frac{R}{L}{i}_d+p\omega i_q+\frac{u_d}{L}\end{array}$ (1)

式中： $\omega$ 为转子机械角速度， $p$ 为磁极对数， ${\psi }_f$ 为转子永磁体在定子上的耦合磁链， $J$ 为折算到电机轴上的等效转动惯量， $i_d$ 、 $i_q$ 为定子电流矢量的 $d$ 、 $q$ 轴分量， $B$ 为粘性摩擦系数， $T_L$ 为负载转矩(由摩擦力矩、惯性力矩叠加折算而成)， $R$ 为绕组电阻， $L$ 为绕组电感， $u_d$ 、 $u_q$ 为定子电压矢量的 $d$ 、 $q$ 轴分量。

3. 电流环内模控制器设计

内模控制器(IMC)的基本结构如图1(a)所示 [2] ， $G\left(s\right)$ 为实际被控对象， $G_m\left(s\right)$ 为被控对象的数学模型， $G_{IMC}\left(s\right)$ 为内模控制器。将 图1(a)变换得到内模控制的等效结构如图1(b)所示。

对(1)进行Laplace变换，得到

$U_d\left(s\right)=Ls{I}_d\left(s\right)+R{I}_d\left(s\right)-Lp\omega I_q\left(s\right)$ (2)

$U_q\left(s\right)=\left(Ls+R\right)I_q\left(s\right)+Lp\omega I_d\left(s\right)+p{\psi }_f\omega$ (3)

由于 ${\psi }_f$ 为常数，可以定义如下的变换：

${U^{\prime }}_q\left(s\right)=U_q\left(s\right)-p{\psi }_f\omega$ (4)

得到：

${U^{\prime }}_q\left(s\right)=\left(Ls+R\right)I_q\left(s\right)+Lp\omega I_d\left(s\right)$ (5)

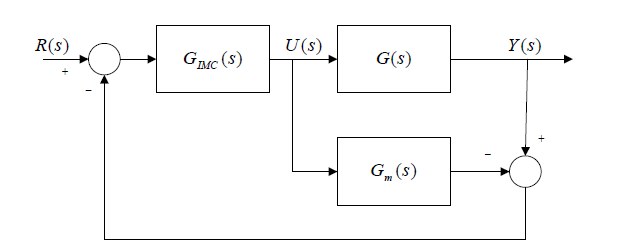(a) 内模控制 (b) 等效反馈控制

Figure 1. IMC and equivalent feedback control structure

图1. 内模控制及等效反馈控制结构

令 $I\left(s\right)=\left[\begin{array}{c}{I}_d\left(s\right)\\ I_q\left(s\right)\end{array}\right]$ , $U\left(s\right)=\left[\begin{array}{c}{U}_d\left(s\right)\\ {U^{\prime }}_q\left(s\right)\end{array}\right]$

可得：

$I\left(s\right)=G\left(s\right)U\left(s\right)$ (6)

其中 $G\left(s\right)={\left[\begin{array}{cc}R+Ls& -Lp\omega \\ Lp\omega & R+Ls\end{array}\right]}^{-1}$

对于PMSM的电流环控制， $R\left(s\right)=I^{*}\left(s\right)$ ( $I^{*}\left(s\right)$ 为给定电流信号)， $Y\left(s\right)=I\left(s\right)$ ，如果 $G_{IMC}\left(s\right)=G^{-1}\left(s\right)$ ，则构成内模控制使得输出 $Y\left(s\right)=R\left(s\right)$ ，输出电流可以直接跟踪给定电流。

由于 $G\left(s\right)$ 中没有纯延迟和右半平面零点，系统稳定。为了使系统具有一定的鲁棒性，可以加上一个前馈低通滤波器 $\Gamma \left(s\right)$ ，则：

$G_{IMC}\left(s\right)=G_m^{-1}\left(s\right)\Gamma \left(s\right)$ (7)

其中 $\Gamma \left(s\right)=diag\left[\frac{{\omega }_c}{s+{\omega }_c},\frac{{\omega }_c}{s+{\omega }_c}\right]$

式中： ${\omega }_c$ 为调节参数。

故设计的内模电流调节器为：

$G_{IMC}\left(s\right)=G_m^{-1}\left(s\right)\Gamma \left(s\right)=\left[\begin{array}{cc}R+Ls& -Lp\omega \\ Lp\omega & R+Ls\end{array}\right]\Gamma \left(s\right)$ (8)

把内模控制的电流调节器等效成图1(b)所示的反馈控制器为

$D\left(s\right)=\frac{{\omega }_c}{s}\left[\begin{array}{cc}R+Ls& -Lp\omega \\ Lp\omega & R+Ls\end{array}\right]$ (9)

则可以得到PMSM电流环内模控制为

$U_d=\left({\omega }_{c}L+\frac{{\omega }_{c}R}{s}\right)I_d-\frac{p\omega {\omega }_{c}L}{s}{I}_q$ (10)

$U_q=\left({\omega }_{c}L+\frac{{\omega }_{c}R}{s}\right)I_q+\frac{p\omega {\omega }_{c}L}{s}{I}_d+p\omega {\psi }_f$ (11)

4. 自抗扰速度控制器设计

自抗扰控制器通过跟踪微分器为给定输入信号安排过渡过程，并提取其微分信号，然后利用扩张状态观测器得到系统内外扰动的估计 [3] [4] 。最后利用非线性反馈控制律得到控制量。首先定义速度环内外扰动：

$d\left(t\right)=-\frac{B}{J}\omega -\frac{T_L}{J}$ (12)

根据(1)，

$\stackrel{\dot{}}{\omega }=\frac{3p{\psi }_f}{2J}{i}_q+d\left(t\right)$ (13)

由(13)可以看出，电机的速度方程为一阶方程，其二阶扩张状态观测器可以设计为

$\{\begin{array}{l}\epsilon =\omega -z_{21}\\ {\stackrel{\dot{}}{z}}_{21}=z_{22}-{\beta }_{01}fal\left(\epsilon ,{\alpha }_1,\delta \right)+bu\left(t\right)\\ {\stackrel{\dot{}}{z}}_{22}=-{\beta }_{02}fal\left(\epsilon ,{\alpha }_2,\delta \right)\end{array}$ (14)

$fal\left(\epsilon ,\alpha ,\delta \right)=\{\begin{array}{ll}{\left|\epsilon \right|}^{\alpha }sat\left(\epsilon \right)\hfill & \left|\epsilon \right|>\delta \hfill \\ \epsilon /{\delta }^{1-\alpha }\hfill & \left|\epsilon \right|\le \delta \hfill \end{array}$ (15)

$sat\left(\epsilon ,\varsigma \right)=\{\begin{array}{ll}\epsilon /\varsigma \hfill & \left|\epsilon \right|\le \varsigma \hfill \\ sign\left(\epsilon \right)\hfill & \left|\epsilon \right|>\varsigma \hfill \end{array}$ (16)

非线性状态误差反馈控制律设计为

$\{\begin{array}{l}{\epsilon }_1={\omega }^{*}-z_{21}\\ u_0={\beta }_{03}fal\left({\epsilon }_1,{\alpha }_3,{\delta }_1\right)\\ u=u_0-z_{22}/b\end{array}$ (17)

式中， ${\omega }^{*}$ 为参考速度， $\omega$ 为输出信号， ${\epsilon }_1$ 为速度误差； $z_{21}$ 为速度的跟踪信号， $z_{22}$ 为扰动信号 $d\left(t\right)$ 的观测值， $u_0$ 为非线性状态误差反馈的输出， $u$ 为系统控制变量， $b=3p{\psi }_f/2J$ ； ${\beta }_{01}$ ， ${\beta }_{02}$ ， ${\beta }_{03}$ 为输出误差的增益； $\delta$ 为扩张状态观测器的滤波系数； ${\alpha }_1$ ， ${\alpha }_2$ ， ${\alpha }_3$ 为非线性因子。

5. 仿真研究

针对某火箭炮交流调速系统，参数如表1所示：

自抗扰控制器的参数设计为： ${\beta }_{01}=5080$ ， ${\beta }_{02}=4100000$ ， ${\beta }_{03}=0.5$ ， ${\alpha }_1=0.8$ ， ${\alpha }_2=0.48$ ， ${\delta }_1={\delta }_2=0.5$ ， ${\varsigma }_1={\varsigma }_2=0.6$ 。内模控制器的参数设计为： ${\omega }_c=4900$ ， $d$ 轴参数变化估计的自适应律的参数设计为 [5] ： $\gamma =0.05$ ， $k_{p1}=11$ ， $k_{i1}=1600$ ； $q$ 轴参数变化估计的自适应律的参数设计为： $k_{p2}=19$ ， $k_{i2}=5100$ 。

为了比较所提出控制策略的有效性，与传统的控制方法进行了仿真比较。传统方法的速度环使用PI控制 [6] ，电流环采用内模控制器；本文提出的控制策略 [7] ，速度环采用自抗扰控制器，电流环采用基于参数变化估计的内模控制器。位置环均采用PID控制。系统在1 s加入阶跃负载干扰14.86 N·m以及系统转

Table 1. Pitch position servo system parameters

表1. 俯仰位置伺服系统参数

动惯量减小50%时，采用传统方法与本文方法的仿真结果如图2，图3所示。1为传统方法的响应曲线，2为本文方法的响应曲线。由以上仿真结果可以看出，本文的自抗扰控制器的位置跟随性能明显好于传统控制器，可以使系统获得更强的鲁棒性和更好的抗干扰性能。

6. 总结

为了实现交流位置伺服系统的高精度位置控制，提出将一种自抗扰内模控制策略应用于交流位置伺

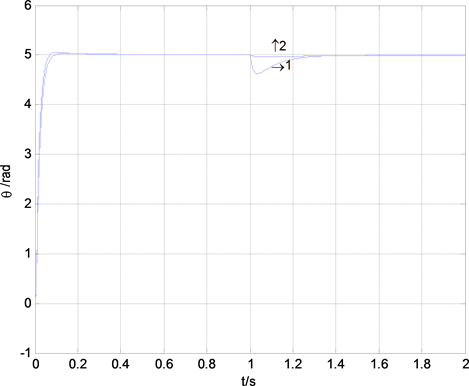
Figure 2. Response curve under exterior load disturbance

图2. 外加负载扰动响应曲线

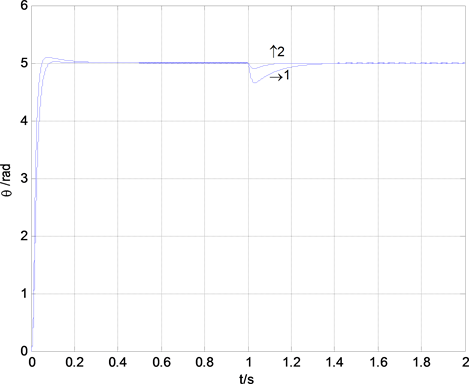
Figure 3. Rotation inertia decrease half

图3. 系统转动惯量减小50%

服系统，以抑制各种不确定因素对受控对象的影响，增强系统的鲁棒性。仿真结果表明，这种控制策略既可以满足伺服系统的跟随特性，又可以有效地抑制干扰，降低系统对参数摄动的敏感程度。采用这种方法后，伺服系统的精度较高、鲁棒性强，可以满足指标要求，具有实际应用前景。

基金项目

项目名称：典型废机电产品协同处置关键技术研究；项目号编号：CE20155058。