一种提高SVM分类能力的同步优化算法

A Synchronous Optimization Algorithm for Increasing Accuracy of SVM Classification

摘要: 近年来，支持向量机(SVM)理论广泛应用于模式分类，然而影响其分类准确率的两个主要因素特征选择和参数优化又是相互影响和制约的。文章提出一种BA + SVM算法，利用蝙蝠算法(BA)来同步完成SVM的参数优化和输入数据的特征属性选择，提高了SVM的分类能力。设计的三种实验方式在10个测试数据集上实验结果表明，BA + SVM同步优化算法与单一进行参数优化或单一进行特征选择算法相比，具有输入特征少分类准确率高的优势。

Abstract: Support vector machines (SVM), which is a popular method for pattern classification, has been recently adopted in range of problems. In training procedure of SVM, feature selection and parameter optimization are two main factors that impact on classification accuracy. In order to improve the classification accuracy by optimizing parameter and choosing feature subset for SVM, a new algorithm is proposed through combining Bat Algorithm (BA) with SVM, termed BA + SVM. For assessing the performance of BA + SVM, 10 public data-sets are employed to test the classification accuracy rate. Compared with grid algorithm, conventional parameter optimization method, our study concludes that BA + SVM has a higher classification accuracy with fewer input features for support vector classification.

1. 引言

支持向量机(SVM) [1] 是一种普遍、高效的模式分类方法，已被广泛应用于文本分类 [2] 、生物信息学和模式识别 [3] 等领域。提高SVM分类准确率面临的两个主要问题是：如何选择核函数的最佳参数，以及如何选择用于训练和测试的最佳特征子集。

提高分类准确率一般有三种方法。其一，优化SVM核函数的参数。具体途径是网格寻优或者使用交叉验证得到SVM的经验参数，并普遍应用于参数选择研究。其二，是对输入样本进行特征选择。因为选择不当的数据特征可能会导致较差的分类精度 [4] 。特征选择是选择输入样本的重要特征，不仅删除了一些冗余甚至无关的特征 [5] ，同时也可提高分类准确率。第三，SVM的参数优化和特征选择同步进行。这种方法是近年来的研究热点。比如，Adriano L.I. Oliveira等 [6] 提出的GA + SVM模型用于机器学习回归的特征选择和参数优化，Huang [7] 和Lin [8] 采用的粒子群优化算法(PSO)来优化特征子集和SVM参数，都取得了有效的成果。最近，Li [9] 采用遗传算法(GA)实现特征选择和优化SVM参数进行网络入侵检测。

蝙蝠算法(BA)是一种具有回波定位特征的元启发式优化算法 [10] 。为了得到优化结果，BA采用频率调整方式，模仿蝙蝠的脉搏和响度的变化，使用自动缩放功能来平衡探索，简化搜索过程。

因此，这就意味着BA比其他算法效率更高。有结果表明基于支持向量机的BA参数优化算法取得了满意结果 [11] 。对这个结果做进一步的研究发现，这种元启发式算法还可以同步实现特征选择和SVM参数优化。文章提出的基于蝙蝠算法的特征选择与参数优化的向量机分类算法，称为BA + SVM。这种方法通过蝙蝠的位置更新方式同步执行特征选择和参数优化，不但优化了SVM参数、选择了适当的样本特征，还提高了SVM的分类准确率。

2. 相关工作

2.1. SVM分类器

给定一组具有标签的样本集 $\left(x_i,y_i\right)$ ， $i=1,2,\mathrm{...},m$ ，其中m是训练数据的个数， $x_i\in R^n$ ， $y_i\in \{-1,1\}$ ，n表示输入样本维数。对线性可分离数据点，SVM可以通过选择最佳分离超平面来进行训练数据分类。

$\langle \omega \cdot x_i\rangle +b=0,i=1,2,\cdots ,m$ (1)

如果存在满足方程式的超平面(1)，通过求解以下的优化问题，可以找到最优线性分离超平面：

$\begin{array}{l}\underset{1\le i\le m}{\min }\frac{1}{2}{\omega }^{\text{T}}\omega +C{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\xi }_i}\\ \text{subjectto}:y_i\left(\langle \omega \cdot x_i\rangle +b\right)-1\ge 0\end{array}$ (2)

其中C是惩罚参数， ${\xi }_i$ 是非负的松弛变量。引入拉格朗日乘数 ${\alpha }_i$ ，原优化问题可以通过其对偶问题来解决。通过求解对偶问题得到 ${\alpha }_{*i}$ ，最后确定最优超平面的参数 ${\omega }_{*}$ 和 $b_{*}$ 。其决策函数的定义如下：

$f\left(x\right)=sign\left({\displaystyle \underset{i=1}{\overset{m}{\sum }}{y}_i{\alpha }_i^{*}\langle x_i\cdot x\rangle }+b^{*}\right)$ (3)

非线性SVM分类器可以表示为：

$f\left(x,{\alpha }_i^{*},b^{*}\right)=sign\left({\displaystyle \underset{i=1}{\overset{m}{\sum }}{y}_i{\alpha }_i^{*}k\left(x_i,x\right)}+b^{*}\right)$ (4)

2.2. 蝙蝠算法

蝙蝠是一种具有回声定位的哺乳动物 [7] ，当蝙蝠在飞行时通过分析返回的回波来导航并检测猎物 [11] 。此外，蝙蝠能够通过回声定位系统获得物体之外的距离，以防止碰撞 [12] 。基于蝙蝠的回声定位特征和觅食行为，Yang [10] 提出了蝙蝠算法。蝙蝠算法的基于以下规则：

规则1：蝙蝠都通过回声定位感知距离，并且能通过某种方式分辨猎物和障碍物。

规则2：蝙蝠在位置 $x_i$ 以速度 $v_i$ 和频率 $f_{\min }$ 随机飞行，通过不断变化的响度 $A_0$ 和频率来搜寻猎物。它们自动调整所发射脉冲频率，并依据距离来调整脉冲发射频率 $r\in \left[0,1\right]$ 。

规则3：虽然响度变化范围可以不同，我们通常假设其从最大值 $A_0$ 减小到最小值 $A_{\min }$ 。

基于以上规则，蝙蝠算法的基本步骤为：

步骤1：初始化基本参数。包括响度衰减系数 $\alpha$ ，脉冲发射强化系数 $\gamma$ ，最大固定频率 $f_{\max }$ ，最小频率 $f_{\min }$ ，迭代次数 $ite{r}_{\max }$ 和种群大小 $N$ ；

步骤2：初始化蝙蝠算子 $i\left(i=1,2,\cdot \cdot \cdot ,n\right)$ 的参数：位置 $x_i$ ，速度 $v_i$ ，固定频率 $f_i$ 和响度 $A_i$ ；

步骤3：当 $t<ite{r}_{\max }$ 时生成新的解决方案，通过公式(8)~(10)更新速度和解决方案；

步骤4：如果 $rand>r_i$ ，从最佳解决方案中选择一个解，并在选择的最佳解决方案周围生成当局最优解，然后通过自由飞行生成一个新的解决方案；

步骤5：如果 $rand<A_i$ 且 $f\left(x_i\right)<f\left(x_{*}\right)$ ，接收新的解决方案，让 $r_i$ 增加并且 $A_i$ 减少；

步骤6：根据其适应度值对蝙蝠进行排名，并找出当前的最佳位置 $x_{*}$ ；

步骤7：如果达到停止条件(即达到最大许可迭代次数或达到搜索精度)，转到步骤8；否则转到步骤3并继续搜索；

步骤8：输出最佳适应值和全局最优解。

假设t时刻蝙蝠i的位置为 $x_i^t$ ，速度为 $v_i^t$ ，那么，蝙蝠算法的更新公式为

$f_i=f_{\min }+\left(f_{\max }-f_{\min }\right)\beta$ (5)

$v_i^{t+1}=v_i^t+\left(x_i^t-x_{*}\right)f_i$ (6)

$x_i^{t+1}=x_i^t+v_i^{t+1}$ (7)

其中 $\beta$ 表示[0,1]中的随机数， $f_i$ 表示当前时刻蝙蝠i的变化频率。这里， $x_{*}$ 是当前的全局最优解。

为了提高解决方案的灵活性，从蝙蝠种群中选择一个蝙蝠，并根据方程(8)，通过蝙蝠的自由飞行来创建一个新的当局解决方案。这种随机游走可以解释为本地搜索过程，用于创建新的解决方案。

$x_{new}=x_{old}+\epsilon A^t$ (8)

其中， $A^t$ 代表蝙蝠群体在t时刻的平均响度， $\epsilon \in \left[-1,1\right]$ 是随机向量。 $x_{old}$ 表示从当前最优解中选择的随机解。

在BA算法的迭代过程中，使用以下方程来更新响度 $A_i$ 和发射脉冲速率 $r_i$ ：

$A_i^{t+1}=\alpha A_i^t$ (9)

$r_i^{t+1}=r_i^0\left[1-\exp \left(-\gamma t\right)\right]$ (10)

其中 $\alpha$ 和 $\gamma$ 是常数，在大部分应用程序中我们通常设置 $0<\alpha <1,\gamma >0$ 。因此，很容易得到，当 $t\to \infty$ ， $A_i^t\to 0$ 时 $r_i^t\to r_i^0$ 。

2.3. 特征选择

特征选择的策略可以分为两种不同的模型，分别称为包装模型和滤波模型的模型 [13] 。与包装模型相比，滤波器模型具有更快的速度。然而，包装模型可有利于找到最好的特征子集 [14] 。

3. 基于BA的SVM特征选择和参数优化

3.1. 蝙蝠位置的表示

使用RBF核函数的SVM来实现BA + SVM方法。蝙蝠位置向量由特征掩码(离散值)和参数掩码(连续值 $C$ 和连续值 $\gamma$ )两部分组成。蝙蝠位置向量的具体设计如表1所示。

其中，n表示数据集的特征数量，输入特征掩码 $x_{i,1}~x_{i,n}$ 是布尔值，“1”表示选择了该特征，“0”表示未选择该特征。 $x_{i,n+1}$ 表示参数 $C$ 的值， $x_{i,n+2}$ 表示参数 $\gamma$ 的值。

3.2. 蝙蝠位置的更新标准

在更新蝙蝠的位置和速度的过程中，速度公式(6)保持不变。对于特征掩码1~n，新的蝙蝠位置的值由以下规则来计算：if $\text{rand}(.)<S\left(v_{i,d}\right)$ ，then $x_{i,d}=1$ ；else $x_{i,d}=0$ ，其中 $S\left(v\right)=\frac{1}{1+{\text{e}}^{-v}}$ 。 $S\left(v\right)$ 是一个sigmoid函数，rand(.)是从[0,1]中选出的随机数。参数掩码的位置公式(7)不变。

3.3. 适应度函数

根据实验，更高的分类准确率和更少的特征数会产生更好的适应度值。因此，设计适应度函数如下：

$fi{t}_i={\omega }_A\cdot ac{c}_i+{\omega }_F\cdot \left(1-\frac{{\displaystyle \underset{j=1}{\overset{n}{\sum }}{f}_j}}{n}\right)$ (11)

${\omega }_A$ 是SVM的分类准确率权重， ${\omega }_F$ 是所选特征数量的权重，用户可根据需要进行适当调整。如果选择了特征j， $f_j=1$ ，否则 $f_j=0$ 。 $ac{c}_i$ 表示SVM分类准确率，由公式(12)给出。 $ac$ 和 $uc$ 分别表示正确分类的样本数和不正确分类的样本数。

$ac{c}_i=\frac{cc}{cc+uc}\times 100\%$ (12)

4. BA + SVM参数优化和特征选择算法

BA + SVM参数优化和特征选择的流程图如图1所示，详细的实验步骤如下：

步骤1：预处理数据：对样本数据做归一化。

步骤2：蝙蝠初始化及SVM参数初始化：即设置蝙蝠算法的参数，包括蝙蝠个数，迭代次数，噪音系数，脉冲强度系数，脉冲频率限制以及适应度函数的权重。以及 $C$ 和 $\gamma$ 的初始值。

步骤3：建立SVM模型并计算准确率：选择用于训练SVM分类器的输入特征，并于计算基于 $C$ 和 $\gamma$ 的平均分类准确率。

Table 1. The composition of the location of the bat i

表1. 蝙蝠i的位置组成表

Figure 1. Flow chart: BA + SVM parameter optimization and feature selection

图1. BA+SVM参数优化和特征选择的流程图

步骤4：更新全局最优解：该模型中每个蝙蝠的适应度值根据公式(11)进行计算。根据适合度值更新全局最优解。

步骤5：判断停止条件：当满足停止条件时，输出最优特征子集和最优参数 $C$ 和 $\gamma$ ；否则，进行下一步。

步骤6：更新蝙蝠算法：根据蝙蝠算法更新每个蝙蝠的速度和位置并搜索更好的解决方案，然后转到步骤3。

5. 实验结果

5.1. 平台和数据集

运行BA + SVM方法的平台是具有以下功能的PC端：Intel Pentium®双核CPU，2.5GHz，2.00GB RAM，Windows 7操作系统，运行环境为MathWorks MATLAB 7.9 R2009b(Windows)，软件为Libsvm [15] 。

为了评估BA + SVM方法的分类能力，使用UCI机器学习库中的10个数据集进行测试，如表2所示。

5.2. 评估方法

停止标准是迭代次数达到500，或适应度值在前100次迭代中没有改善。

多分类问题的准确率一般通过总体命中率进行评估，两分类问题的准确性评估一般需要三个指标进行详细说明，表3给出两分类问题的分类情况。

Table 2. UCI machine learning library data set

表2. UCI机器学习库的数据集

Table 3. Classification of the two categories of issues

表3. 两分类问题的分类情况

TP和FN分别表示正样本的正确分类率和正样本的不正确分类率，是两个重要的性能指标，计算公式表示如下：

$\text{TP}=\frac{\#\text{TruePositive}}{\#\text{FalseNegative}+\#\text{TruePositive}}$ (13)

$\text{TN}=\frac{\#\text{TureNegative}}{\#\text{TrueNegative}+\#\text{FalsePositive}}$ (14)

$\text{Averageaccuracy}=\frac{\#\text{TruePositive}+\#\text{TruePositive}}{\#\text{TestingSample}}$ (15)

5.3. 实验结果

设计了三种实验方式，如表4所示。实验中，BA群体大小为20，响度衰减系数为 $\alpha =0.5$ ，脉冲发射系数为 $\gamma =0.5$ ，脉冲频率限制为 $f_i\in \left[0,2\right]$ 。SVM中参数 的搜索范围为0.01~10000，参数 $\gamma$ 的搜索范围为0.01~1000。适应度函数中， ${\omega }_A=0.8$ 和 ${\omega }_F=0.2$ 。

表5结果显示，BA + SVM和PSO + SVM在不同数据集上产生比SVM更高的分类准确率，说明这两种组合算法确实可以获得更好的SVM参数和特征子集。此外，在没有特征选择的情况下，BA + SVM在6个数据集中产生较高的分类准确率。进行特征选择的情况下，BA + SVM在7个数据集中产生较高的分类准确率。一般来说，同步进行参数优化和特征选择的BA + SVM比PSO + SVM具有更好的性能。

网格算法是一种常规的参数优化方法。表6列出的是蝙蝠算法的参数寻优和网格算法的参数寻优比较结果。对于二分类数据集，BA寻优的平均正命中率和平均负命中率均高于网格寻优算法。

图2(a)到图2(d)显示了4个数据集中三种优化方法的测试结果。显然，在选择的四个数据集上，同

Table 4. Experimental design

表4. 实验方式设计

Table 5. Comparison of classification results between BA + SVM and SVM and PSO + SVM

表5. BA + SVM与SVM和PSO + SVM的分类效果比较

Table 6. Comparison of BA optimization and grid optimization without feature selection

表6. 无特征选择情形下BA寻优和网格寻优对比

步进行参数优化和特征选择的BA + SVM具有最高的分类准确率，这表明同步优化的BA + SVM具有最优性能。

6. 结论

输入样本的特征选择和SVM核函数的参数设置是彼此相互影响的，提出的参数寻优和特征选择的同步算法就是为了解决这一博弈问题。仿真实验表明，无论是否进行特征选择，BA + SVM都具有比PSO + SVM

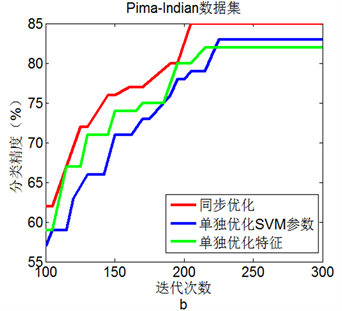
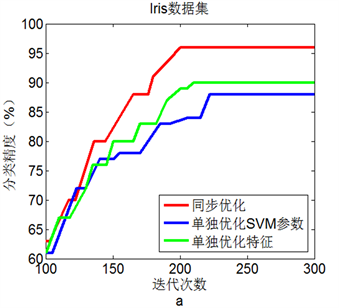
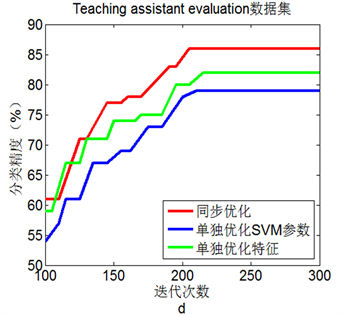
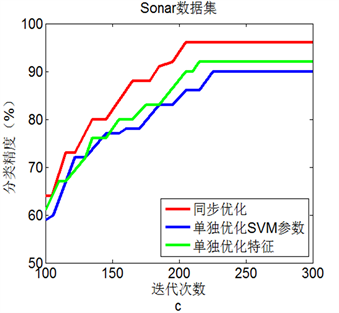
Figure 2. Line chart: Comparison of three experimental results on 4 data sets

图2. 4个数据集上三种实验结果比较

更高的分类准确率。就单纯参数优化而言，BA + SVM有比网格寻优具有更好的SVM分类准确率。此外，4个数据集上的仿真实验表明，同步进行参数优化和特征选择的BA + SVM比单独进行参数优化或特征选择的BA + SVM具有更好的分类效果。

基金项目

国家自然科学基金项目(11301492)；中国地质大学(武汉)基础研究基金项目(CUGL140420)。