1. 引言
1965年,英国渡桥热电厂的8座冷却塔群在暴风中倒塌了后排的3座,研究人员认为是前排冷却塔的干扰效应引起后排冷却塔风荷载的显著增大,从而导致后排3座塔的破坏 [1] 。此后干扰效应研究成为结构风工程领域的热点之一 [2] [3] [4] [5] 。已有的研究表明:群体建筑的干扰效应在某些情况下会使得结构上的风荷载和风致响应增大。中国规范 [6] 、澳洲规范 [7] 、欧洲规范 [8] 和ASCE规范 [9] 等均对干扰问题进行了一定程度的规定。但是,由于干扰问题的复杂性及多样性,对超过3栋的建筑群体,干扰效应还难以获得定量的结论,目前这方面的研究主要是针对具体工程问题 [10] [11] [12] [13] [14] 。
某超高层建筑位于珠江新城——广州市21世纪中央商务区,西部毗邻广州东塔,南部紧挨丽丝卡尔顿酒店,屋面设计高度为308米,总建筑面积约为15万平方米。该高层建筑结构设计采用带加强层的钢管混凝土框架-钢筋混凝土核心筒结构。广州地区是台风多发地区,风荷载是该楼结构设计的控制荷载。由于该高层建筑地处广州市CBD的中心地带,建筑物周围高层建筑十分密集,风效应比较复杂。因此,周围建筑对该主体建筑的干扰效应不能忽视。为准确获取结构设计所需要的风荷载,采用刚体模型同步测压(SMPSS)试验方法对该超高层建筑开展了风洞试验研究。基于试验结果对建筑物表面风压及风致响应的干扰效应进行了详细研究,其结果可为类似密集建筑群区域新建超高层建筑抗风设计提供参考。
2. 试验简介
2.1. 试验设备及流场模拟
本次试验是在湖南大学教育部建筑安全与节能重点实验室的大气边界层风洞试验室中进行。边界层风洞的截面为3.0 m × 2.5 m (宽 × 高)的矩形,试验段的风速在0~20.0 m/s内可调。试验中选用被动方法模拟流场,采用二元尖塔和粗糙元来模拟大气边界层平均风速和湍流强度分布。根据该高层建筑物周围的地貌情况,并结合我国建筑结构荷载规范(GB50009-2012) [6] 中对地面粗糙度的分类规定,在本次试验中模拟了相应的C类地面粗糙度风场。图1为流场调试后得到的C类地面粗糙度的平均风速剖面和湍流强度分布剖面。图2为参考高度处的脉动风速功率密度谱,可以看出,风洞试验模拟的风速功率谱与Karman谱吻合得较好。
2.2. 试验模型
风洞试验模型是用ABS板制成的刚体模型,几何外形与实际建筑保持相似。主体模型具有足够的强
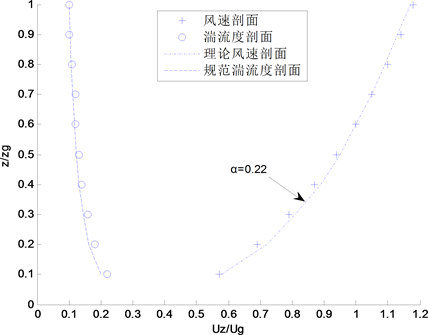
Figure 1. Mean wind velocity and turbulence intensity
图1. 平均风速和湍流度剖面
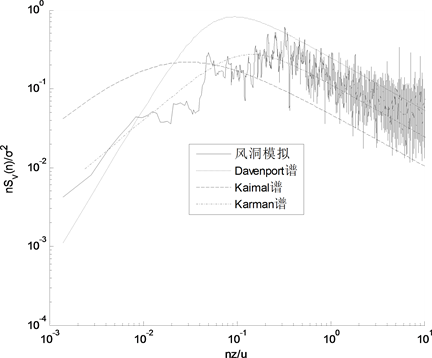
Figure 2. PSD of fluctuating wind velocity
图2. 顺风向脉动风速功率谱
度和刚度,在试验中不会发生明显的变形和振动现象,可以保证压力测量的精度。试验模型缩尺比为1:500,周边模型缩尺比也为1:500。主体模型和周边模型具体相对位置及风向角定义参见图3。风洞试验模型如图4所示。为测取建筑物的表面风压,在主模型表面上共布置了422个测点,沿高度上密下疏分布14层。
2.3. 试验工况
测压试验分两种情况进行:第一种为单体情况(不考虑周边建筑物的影响);第二种为干扰情况(考虑

Figure 3. Model site and wind direction illustrations
图3. 模型位置及风向角示意图
周边建筑物的影响)。两种情况下,风向角均从0˚到360˚变化,变化间隔为15˚。试验过程中,每个角度各测点风压时程采样频率为312.5 Hz,满足文献 [15] 提出的信号采样频率的要求,采样时间为32秒,即每个测点在每个风向角下记录了10,000个风压时域信号数据。试验参考点高度选为61.6 cm (与模型顶部同高),参考点控制风速为10 m/s。
3. 风压系数分布特性
3.1. 风压系数定义
模型试验中符号约定以压力向内(压)为正,向外(吸)为负。建筑表面各点的风压系数由下列公式给出:
(1)
式中,
是试验模型上第i个测压孔所在位置的风压系数,
是该位置上测得的表面风压值,
和
分别为参考点处测得的平均总压和平均静压。
对于脉动风压,可以通过公式(2)来求得脉动风压均方根值
:
(2)
其中,
为第i个测压孔所在位置的风压差系数时程,N为样本数。
3.2. 平均风压系数
由于来流分离、漩涡脱落以及再附着等因素,建筑表面的风压分布比较复杂,压力分布云图是描述风压分布特性的常用手段。图5给出了主模型在典型风向角下(225˚)平均风压系数的分布云图。图6则给出了主模型在该风向角下脉动风压系数的分布云图。
从图5中可以看出,当来流风向为225˚时,迎风面的平均风压系数与已有的研究成果基本一致 [16] 。在迎风面的边缘处,由于主体建筑的切角效果,出现部分负压。在建筑物的顶部,气流经过上游东塔发

Figure 5. Mean wind pressure coefficients for typical wind direction
图5. 典型风向角下的平均风压系数分布
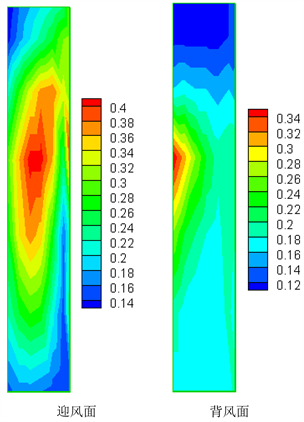
Figure 6. Fluctuating wind pressure coefficients for typical wind direction
图6. 典型风向角下的脉动风压系数分布
生漩涡脱落现象,脱落的漩涡正好撞击主体建筑的右端,导致顶部右端出现较大的正压(0.8到0.9之间)。背风面的平均风压系数在中上部比较小,其绝对值比单个孤立建筑背风面平均风压系数的绝对值要大(孤立建筑在−0.5左右 [16] ),这主要是由于在该风向来流作用下,主体建筑同时受到下游建筑的阻塞影响和主体建筑自身与左侧J2-5建筑(高度约为240 m)并列形成的“峡谷风”效应,增大了主体建筑的尾流风速,导致背风面的风“吸力”增大。值得注意的是,“吸力”增大的现象在与J2-5顶部同一高度处尤其明显。
3.3. 脉动风压系数
从图6中可以看出,当来流风向为225˚时,迎风面的脉动风压系数在0.14和0.40之间,较大的脉动风压系数出现在主体建筑的中上部,这应该与气流流经上游东塔后脱落的漩涡导致紊流增大有关。背风面的脉动风压系数大多在0.12和0.25之间,值得注意的是,在与迎风面出现较大脉动风压系数的同一高度处,背风面的左侧边缘处脉动风压系数也出现了较大值(0.30和0.34之间),这主要是由于侧面的J2-5建筑的绕流造成。可以看出:周围建筑物的干扰效应,尤其是东塔,导致主体建筑表面的脉动风压发生了显著变化,这点在下文的风致响应中还将做进一步讨论。
4. 风致响应
4.1. 平均风响应
任一方向上的平均风致响应可以通过平均风荷载和影响函数得到:
(3)
式中,
表示在结构z高度处α方向上的某一响应均值;
表示α方向上h高度处的平均风荷载;
表示在α方向上h高度处作用单位力在z高度处产生的某一响应值,如式(4)所示:
(4)
其中,
和
分别表示α方向上z和h高度处的第j阶振型坐标,
表示α方向上第j阶广义刚度。需要说明的是:在竖向悬臂结构中,一般只考虑结构第一阶振型的影响。
4.2. 脉动风响应
工程中通常将高层建筑物抽象为一维悬臂的无限自由度体系。采用振型关于质量和刚度的正交特性,同时假定振型关于阻尼正交,高层建筑的运动微分方程可表示为:
(5)
式中,
,
分别为第j阶振型对应的无阻尼自振频率和阻尼比,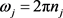 ,
,
分别为第j阶振型对应的广义质量和广义荷载。对于无限自由度体系:
,
,
分别为第j阶振型对应的广义质量和广义荷载。对于无限自由度体系:
(6)
(7)
根据随机振动的振型分解法,任意高度z处的水平响应 (位移、剪力、弯矩等)可表示为:
(位移、剪力、弯矩等)可表示为:
(8)
表示结构在α方向(顺、横风向和扭转方向)上第j阶振型对应的惯性力在z高度处的响应,采用式(2)的影响函数,则
可写作如下统一表达式:
(9)
按振型分解随机振动理论,响应的功率谱密度函数
为:
(10)
(11)
(12)
为广义力互谱密度函数,
(13)
为广义脉动荷载互功率谱。
脉动风响应的方差为:
(14)
背景响应相当于结构忽略了动力放大对脉动激励的响应。根据背景响应的物理意义
,可得到背景响应的方差为 [17] :
(15)
高层建筑发生侧向振动时,结构各自振频率间比较稀疏,阻尼比相对较小,第j阶振型的响应与第k阶振型响应的耦合性很小。因此,可忽略式中响应的交叉项,则有:
(16)
高层建筑风致响应谱在结构自振频率处具有与结构传递函数类似的峰值。因此,在计算共振响应的方差时,可将自振频率附近的响应谱值按白噪声假定简化计算。忽略交叉项后结构任一阶振型对应的共振响应的方差可简化为:
(17)
其中,
为广义脉动荷载功率谱。
需要说明的是:一般高层建筑的风致共振响应主要以第一阶响应为主,第二阶以上的共振响应可以忽略。
4.3. 总的风致响应
结构总的风致响应由平均风响应和峰值脉动风响应叠加而成,一般采用平方和再开方方法(SRSS)计算:
(18)
为平均风响应,按式(3)计算,
和 则按式(14)和式(17)计算。
、
分别为背景峰值因子和共振峰值因子。背景峰值因子只与脉动风本身的统计特性有关,通常可取为3.5;共振峰值因子与共振响应的动态特性有关,按Davenport给出的公式计算:
则按式(14)和式(17)计算。
、
分别为背景峰值因子和共振峰值因子。背景峰值因子只与脉动风本身的统计特性有关,通常可取为3.5;共振峰值因子与共振响应的动态特性有关,按Davenport给出的公式计算:
(19)
其中,
为结构一阶自振频率,T为脉动风时距,一般取600秒。
4.4 结果分析
4.4.1. 基底弯矩
图7(a)~7(d)分别给出了主体建筑模型在单体情况、干扰情况下的基底弯矩响应随风向角的变化曲线。
从图7(a)可以看出,单体情况下,结构相对于y轴对称,Mx的平均分量相对于225˚风向角呈对称分布,My呈反对称分布,这说明本次试验的结果是可靠的。当风向角为45˚或225˚左右时,Mx为顺风向作用,My为横风向作用,此时可以看出,顺风向平均分量的绝对值接近于极大值,横风向平均分量则基本接近于零;反之亦然,当风向角为135˚和315˚左右时,Mx平均分量接近于零,My平均分量接近于极值。干扰情况下,结构顺风向和横风向的基底弯矩平均分量的绝对值大多都比单体情况下要小,这主要是由于周边建筑物产生了“遮挡”效应。最显著的“遮挡”效应发生在135˚和180˚,Mx的平均分量减小了0.53,My的平均分量减小了0.64。但是,在120˚风向角时,干扰情况下的Mx与单体情况相比出现了受力方向相反的情况,这可能与上游的J2-5与主体建筑距离太近有关,气流流经两栋建筑物之间的“走廊”时,发生空气压缩膨胀,导致主体建筑受到与单体建筑相反的横向力作用。45˚风向角时,Mx的平均分量减小了0.04,My的平均分量增大了1.53。此时,东塔正好位于主体建筑的下风向位置,主体建筑的尾流受到东塔的干扰,导致主体建筑的横风向作用增大。225˚风向角时,Mx的平均分量减小了0.06,My的平均分量增大了1.88。此时,东塔正好位于主体建筑的上风向位置,气流流经东塔后发生漩涡脱落,主体建筑正好位于漩涡脱落区,横风向作用明显增大,这点正好与上文中的脉动风压增大的现象吻合。从图7(b)中可以看出,单体情况下,基底弯矩Mx的背景分量在135˚和315˚风向角下出现最大值,基底弯矩My的背景分量在45˚和225˚出现最大值。图7(c)中的共振分量在单体情况下随风向角的变化规律不明显,但是在干扰情况下共振分量则表现出明显的横风向受扰特性。Mx的共振分量在135˚和315˚风向角附近增大,这主要是由于对应风向角的上游建筑的阻塞导致主体建筑周围的脉动风能量加强而致。My的共振分量则在45˚和225˚风向角也出现峰值(45˚风向角增大1.07倍,225˚风向角增大0.24倍),这与上文中提到的主体建筑受东塔干扰是一致的。另外,总体来看,共振分量明显比背景分量大,相差较大时共振分量约为背景分量的3.16倍。这个结果再结合式(18)可知,最终是共振分量在总响应中占主要作用。图7(d)中的基底峰值弯矩Mx、My在单体情况下的变化规律与平均分量基本一致(除240˚风向角外),这说明在单体情况下,平均分量对基底峰值弯矩的贡献较大。在240˚风向角,基底峰值弯矩My出现突变,这主要是由于该风向角下的风致响应是由横风向控制的。值得注意的是,由于该风向角下突变的基底峰值弯矩并未超过全风向角下的基底峰值弯矩最值,所以在结构设计时容易被忽略。干扰情况下,基底峰值弯矩Mx 在120˚和330˚风向角附近出现两个最大值,均表现为横风向风振效应,这点正好与共振分量的变化规律一致,也间接证明了共振分量在总响应中所占比例较大。其中,120˚风向角下的基底峰值弯矩Mx的绝对值为单体情况下对应风向角下基底峰值弯矩的1.83倍,这点在结构设计时应引起重视。基底峰值弯矩My的变化规律与共振分量My也较为一致,但总体而言,相互干扰主要表现为“遮挡”效应。
4.4.2. 基底峰值弯矩与模态阻尼比的关系
根据式(17)可知,模态阻尼比对基底弯矩响应的影响主要体现在共振分量上。图8给出了单体情况下阻尼比为0.035以及干扰情况下阻尼比分别为0.035、0.04、0.05的基底峰值弯矩随风向角的变化曲线。可以看出:随着阻尼比的增加,基底峰值弯矩Mx、My均逐渐减小,这与式(17)、式(18)所表达的物理意义是一致的。但是,峰值响应随模态阻尼比的变化并没有直接的物理公式,这主要是由于峰值响应不仅取决于平均分量、背景分量和共振分量的大小,而且与这三者在峰值响应中所占比例有关。
4.4.3. 峰值加速度
高层建筑在风荷载作用下的人体舒适度,不仅与结构的加速度响应有关,还与结构的自振频率有关 [18] 。但是,对于以弯曲型振动为主的高层建筑,起决定作用的是结构顶部峰值加速度。各种工况下结构顶部峰值加速度的结果如表1所示。从表中可以看出:单体情况下和干扰情况下,结构顶部峰值加速度均由横风向控制。有干扰时,结构顶部最大峰值加速度ay,max为0.348 m/s2,是单体情况下的1.62倍,产生

Figure 8. Base moments as a function of the approaching wind direction at different damping ratio
图8. 不同阻尼比下基底弯矩随风向角变化

Table 1. Maximum of peak acceleration at the top of structure
表1. 结构顶部最大峰值加速度
该最大值的风向角为120˚,和图7(d)所显示Mx产生的干扰效应所对应的风向角一致。我国《高层建筑混凝土结构技术规程》(JGJ3-2010)规定重现期为10年的结构顶点最大加速度限值为:0.15 m/s2(住宅、公寓)和0.25 m/s2 (办公、旅馆)。因此,在有干扰情况下,按规范规定的10年重现期的基本风压(0.30 kN/m2)计算的结构顶部峰值加速度超过了人体舒适度的要求。但根据广东省气候中心提供的气象观测结果(风玫瑰)显示,10年重现期不同风向的最大风速并不相同。如果考虑到这个因素,按有干扰情况重新计算结构顶部x向最大加速度为0.198 m/s2,y向最大加速度为0.234 m/s2,均能满足规范限值要求。
5. 结论
广州珠江新城地区高层建筑密集,高层建筑之间的相互干扰问题十分复杂。本文通过对该地区某超高层建筑进行刚性模型测压风洞试验,仔细研究了单体情况下和干扰情况下的建筑表面风压分布规律,同时利用随机振动理论在频域内计算了结构基底弯矩响应和顶部加速度响应。通过本文的研究可以得到以下结论:
1) 考虑周围建筑物的干扰效应时,主体建筑物的表面风压分布与单体情况下不完全相同。“峡谷风”效应和尾流受扰均会导致主体建筑表面风压系数的增大。
2) 干扰情况下,基底弯矩的平均分量大多呈现“遮挡”效应而减小;基底峰值弯矩由横风向控制,基底峰值弯矩的最大值为对应风向角单体情况下的1.83倍。
3) 结构顶部最大峰值加速度由横风向控制;按风玫瑰结果计算的顶部最大峰值加速度可以满足规范要求。
基金项目
国家自然科学基金项目(51178179)。