1. 引言
近些年,利用WIFI信号进行呼吸检测已经取得了很多研究成果 [1] [2] [3] [4] ,但普遍缺乏有效的理论指导,实验结果的稳定性和再现性难以提高。
最近,在视距范围(line of sight, LOS)环境下基于信道状态信息(Channel State Information, CSI)的相关研究工作中引入了菲涅尔区理论,标志着基于WIFI信号的呼吸检测相关研究工作正由基于模式逐渐过渡为基于模型的阶段 [5] 。基于CSI的菲涅尔区理论目前已被用于室内定位 [6] 、移动方向侦测 [7] 和呼吸检测 [8] 等方面,实践证明该理论的确有利于指导模型设计和实验分析,有效提高了实验的稳定性和再现性。
文献 [8] 通过菲涅尔区理论详细论证了基于WIFI信号的呼吸检测原理,并对双人模式下呼吸检测进行了探索,尽管文中已建立了相对完善的呼吸检测模型,但其所述模型依旧存在一些不足之处:模型在应用时,需计算以决定天线如何放置;实验空间需求大;多人模式下解决方案的前提条件过于苛刻,要求多人的呼吸频率各不相同等等。此外,智能健康设备有着广泛的市场前景,无线信号具有检测范围广、光线条件零敏感度、高隐私保护性、免穿戴等特点,十分符合呼吸频率检测这一特殊场景的种种要求。因此,有必要进一步完善基于菲涅尔区的呼吸检测模型。
本文通过对菲涅尔区特征的进一步分析,并结合不同增益规格下天线的电磁场辐射形态特征,提出了一种基于WIFI信号的呼吸检测模型,简称WI-BD模型。本文后续内容为:第2节介绍基础理论;第3节介绍实验设定和理论分析;第4节介绍WI-BD模型及单目标验证;第5节为全文总结。
2. 模型的理论准备
2.1. 菲涅尔区模型
信号在LOS环境中传播过程中可能会发生反射、衍射和散射等三种现象,但在文献 [9] 中,作者通过模型和实验,证明反射是主要因素,可以忽略衍射和散射带来的影响。
在LOS环境中,由于反射现象是主因,可得信号传播模型如图1所示,其中,点A表示发射天线Tx的位置,点B表示接收天线Rx的位置,点M表示信号反射点。信号从天线Tx发出,经路径D1和路径D2到达接收天线Rx,将路径D1称为直射路径,以
表示其长度;将路径D2称为反射路径。
三维空间中每个点都可作为反射源,反射与直射路径长度相差整数倍半波长的反射点可构成多个曲面,这些曲面将空间分割成不同的有限区域,称为菲涅尔区。根据上述定义得公式如下:
(1)
天线位置固定,所以
是常量,λ表示载波波长,为常量。任意给定i,公式(1)符合椭圆定义。考虑空间是三维,对任意给定的i,符合约束的点都将构成新椭球面,所分割出新有限区域称为第i菲涅尔区,共同焦点是A和B。以任意同时过焦点A和焦点B的平面与各菲涅尔区分界面相交后,如图2所示,其中,O表示点A和点B的中间位置。图中每个椭圆均代表一个菲涅尔区边界,将椭圆上各方向上相邻椭圆间的距离称为该方向上的菲涅尔区半径,比较特殊的是第一菲涅尔区,其各方向上的菲涅尔区半径为第一菲涅尔区边界到线段AB上的最短距离。
为了定量分析各方向上菲涅尔区半径的分布特点,以最特殊的x方向和y方向为例(本文中x方向和y方向均包括正、负方向)。点Tx到各椭圆的最短距离记为
,O到各椭圆的距离记为
,相应的计算公式为:
(2)
(3)
通过公式(2)和(3)可以计算出相应菲涅尔区半径,以
、
为例,可得x方向上和y方向上的菲涅尔区半径如图3所示。
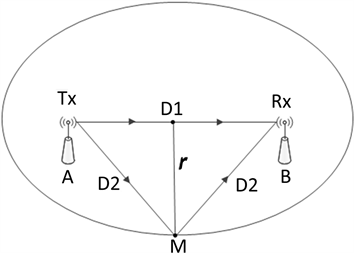
Figure 1. Signal propagation model in LOS environment
图1. LOS环境中信号传播模型
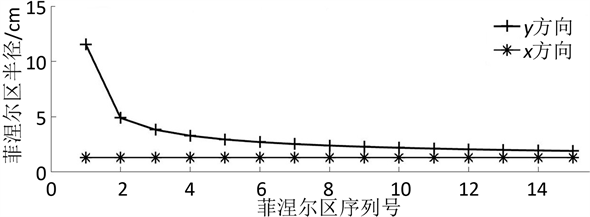
Figure 3. The change of Fresnel zone radius
图3. 菲涅尔区半径变化示意图
2.2. 自由空间传播损耗计算
如果信号在一个无障碍的自由空间中传播,则信号因传播路径长度变化发生的路径损耗PL符合公式(4) [10] :
(4)
WIFI信号的载波频率固定不变,因此F为常量。于是结合公式(4)可知,传播距离D越大,路径损耗越高。经过计算,大约传播距离增加一倍,信号能量强度衰减6 dB。
2.3. 常见WIFI天线物理特征
常见WIFI天线外部形态基本为条状,内部金属构件一般可分为螺旋和直条两个部分,属于电偶极子天线,信号的有效发射区域位于金属构件的直条部分 [11] 。
天线的增益规格有多种,如3 dB、7 dB、11 dB等等。天线增益规格越高,主瓣约束集中程度越高,传播距离越远,副瓣则受到更多抑制,可近似忽略副瓣的存在 [11] ,反映在信号的有效覆盖区域竖直剖面上,增益规格越低的天线在竖直方向上有效覆盖范围越大,在水平方向上有效覆盖围则越小,而增益规格越高天线的信号有效覆盖区域特征反之。
3. 实验设定的理论分析
文献 [8] 通过理论分析和实际实验指出呼吸位移最佳发生位置为单个菲涅尔区的中间区域,但并未证明呼吸最大位移是否可以位于单个菲涅尔区中。对于第一菲涅尔区,由数学知识易知最短菲涅尔半径在x方向上,具体证明过程略;对于第m菲涅尔区:
设天线Tx和Rx坐标分别为
和
,即有
,代入公式(1)可得:
(5)
其中,
,
。
对公式(5)求导,并代入
和
,可得椭圆的切线斜率:
(6)
椭圆具有对称性,可按象限分成相同的四个部分。以第一象限为例进行分析,θ的取值范围为0至0.5 π,在此区间内,k随θ增大而单调递增。第m菲涅尔区介于第m菲涅尔边界和第m − 1菲涅尔边界之间,由公式(6)可知图2中第m椭圆切线斜率
和第m − 1椭圆切线斜率
:
(7)
(8)
令
,
,代入公式(7)和公式(8),则有:
(9)
已知
,则有
,又由
可知
,所以对于公式(9),可知:
。又因椭圆切线在第一象限时的斜率均为负数,可得:
。
由于椭圆斜率在第一象限是单调递增,且对于任意θ都有
,则随θ增大,第m椭圆和第m-1椭圆上的点呈远离趋势,如图4所示。于是可知椭圆间距离最近的方向为x方向,椭圆间距变化在其他象限的变化趋势可参照第一象限。所以,第m菲涅尔区的最短菲涅尔区半径同样也在x方向上。
由公式(2)可知,x方向上的所有菲涅尔区半径大小均为四分之一波长,常见WIFI天线的中心工作频率约为2.4 GHz和5.35~5.8 GHz,波长分别约为12.5 cm和5.6~5.2 cm,可得相应最短菲涅尔区半径大小分别为3.125 cm和1.4~1.3 cm。经人工测量,呼吸时腹部轮廓正向变化幅度约为5~10 mm,因此腹部呼吸位移完全可以位于2.4 GHz和5.35~5.8 GHz载波的任一菲涅尔区中。如果个别人员呼吸时腹部位移特别大或特别小,可根据具体数值,选择具备合适波长的载波,即选择合适频率的载波。
当呼吸产生的位移完全位于单个菲涅尔区中时,可得公式(10):
(10)
在单菲涅尔区中,若反射信号和直射信号之间的相位差越大,则CSI变化幅度越大。呼吸位移大小是由个人生理因素决定,可视为定值。通过公式(10)可知,若要获得最大相位差,就应使菲涅尔区半径尽可能小,而x方向有最小的菲涅尔区半径,所以x方向是最佳检测方向,可获得最佳菲涅尔半径。且由公式(2)可知,x方向上的菲涅尔区半径大小与天线间距无关,使得天线Tx和Rx之间的距离完全可根据实际情况的需要进行自由调节。
为了量化分析天线间距对天线有效监测区域大小的影响,本文设计了一个实验:在LOS环境中,天线Tx和Rx离地高度100 cm,实验人员四处走动,不经过天线Tx和Rx之间的区域,将对CSI的干扰幅度大于0.5 dB的区域视为有干扰区域。经实验测定,不同天线间距与天线有效监测区域范围对应关系如表1所列,表1中横向表示x方向,纵向表示y方向。
从表1中的数据可以明显看出随着天线Tx和Rx之间的距离增加,监控区域范围迅速增大,x方向的有效监控范围明显小于y方向,完全符合菲涅尔区的分布特征。
由于反射信号对直射信号的干涉是CSI分布产生变化的主要因素。由公式(4)可知,直射路径长度和载波频率不变时,信号强度在直射路径上传播损耗率是恒定值,当反射信号强度低于一定值后,将无法对直射信号形成有效干扰,于是易知直射路径越短,有效的反射路径同样会越短,表1中的数据证明了这一结论。
文献 [1] [2] [3] [4] 并未研究检测方向对检测效果是否存在影响,文献 [8] 选择y方向作为模型的呼吸频率检测方向,而本文将采用x方向作为呼吸频率检测方向,可获得最小菲涅尔区半径,不需要预先计算y方向各菲涅尔区半径大小,且通过调节天线间距可有效控制天线的有效监控范围,尽量避免目标之外的人员活动干扰。
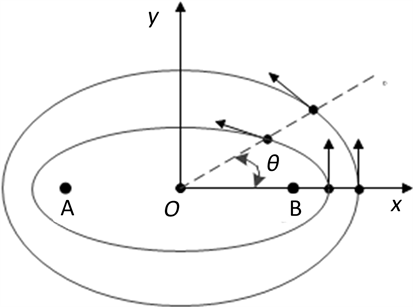
Figure 4. The distance change of common focus ellipse
图4. 共焦点椭圆间距变化

Table 1. Antenna spacing and detection area radius (unit: cm)
表1. 天线间距与检测区域半径(单位:cm)
此外,外层菲涅尔区相比于内层菲涅尔区具有更长的反射传播路径,由公式(2)可知,反射信号由外层菲涅尔区到达天线Rx时信号强度值更低,而x方向上的菲涅尔区半径均相等,因此可选择内层的菲涅尔区,优于其他研究工作中只能选择中外层菲涅尔区。
综合来说,选择x方向可以获得更佳的观测效果和更好的抗干扰性。
4. WI-BD模型简介及验证
4.1. WI-BD模型简介
WI-BD模型的具体结构如图5所示。
第一部分是实验布置。通过前述数学分析过程,本文确立以x方向作为呼吸检测方向,参考表1中数据,为了兼顾实验过程中抗干扰性和天线工作稳定性,天线间距一般取值20~50 cm。考虑到不同增益规格下天线物理特征存在差异,所以天线摆放位置与具体睡姿相关,后续章节将给出针对性解答,实验布置完成后,转入第二部分。
第二部分是信号采集。使用与网卡配套的软件工具采集CSI,采样频率f一般选取20~100 Hz,在数据采集的开始阶段,观察CSI波形变化,细微地调节呼吸形变区域和天线之间距离,让呼吸过程中所发生的位移完全落入单个菲涅尔区中,当获得明显呼吸波形后,转入第三部分。
第三部分是降噪处理。由于室内多径效应和设备自身原因等因素影响CSI,需要对原始CSI使用降噪算法进行处理,常用降噪算法有:Butterworth低通滤波、PCA降噪、滑动平均滤波等。本文所述模型采用滑动平均滤波算法和Butterworth低通滤波。降噪后转入第四部分。
第四部分是提取呼吸频率。参考文献 [12] 中方案,本文提出一种瞬时呼吸频率提取算法用于瞬时呼吸频率提取。
瞬时呼吸频率提取算法的具体步骤如下:
输入:子载波序列
,采样频率f。
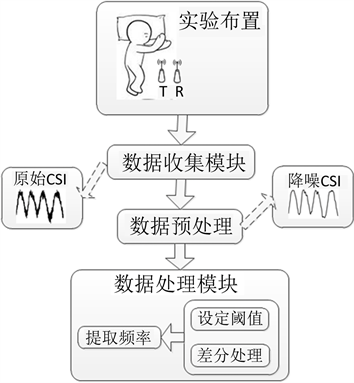
Figure 5. The structure of WI-BD model
图5. WI-BD模型结构
输出:瞬时呼吸频率序列
。
1) 初始化。任意选择第k子载波进行差分处理,生成差分序列
。
2) 合并单调区间。令
,
,
;将差分序列中相邻同为正或同为负的数值合并成一个区间,以区间累加值
以及合并数值个数
表示第i区间,可得累加值序列
和计数序列
。
3) 若t小于r,从位置t开始,在累加值序列中找到第一个大于给定阈值
的
作为吸气阶段起始位置;否则退出算法。
4) 从
开始,尝试累加
和
,若s等于r,则退出算法;若在b处有
的累加值大于
,且
的累加值不大于
,则认为找到吸气阶段,更新
,若P为0,则
,否则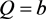 ;否则,
,转3)。
;否则,
,转3)。
5) 若t小于r,从位置t开始,在累加值序列中找到第一个小于给定阈值
的
作为呼气阶段起始位置;否则退出算法。
6) 从
开始,尝试累加
和
,若s等于r,则退出算法;若在d处有
的累加值小于
,且
的累加值不大于
,则认为找到呼气阶段,更新
;否则
,
,转3)。
7) 若P为0,则
,转3)。
8) 累计
至
,记为S。则有
,更新
,
,转3)。
瞬时呼吸频率提取算的法设计依据是呼吸周期会符合一定规律:呼吸周期一定具备吸气阶段和呼气阶段,且吸气阶段一定先于呼气阶段;吸气阶段和呼气阶段的持续时长有限,且呼吸停顿时长也有限;吸气阶段CSI呈快速上升趋势,呼气阶段CSI呈快速下降趋势;吸气阶段和呼气阶段的CSI变化幅度大致相等。阈值主要为经验值,比如,根据观察结果设置CSI变化幅度阈值。一般单次睡眠过程中腹部轮廓的变化幅度比较稳定,且本文所述模型在应用中具有显著的CSI变化,与环境背景噪音所造成的CSI变化具有明显区别,因此可选低于实际幅度的值作为阈值。
4.2 模型验证
本文选取常见的平卧和侧卧两种姿势对所述模型进行验证,依据前述理论分析,并结合常见WIFI天线电磁场特征,实验布置如图6所示。
实验布置具体要求:当实验对象处于平卧状态时,天线Tx和Rx放置方式如图6(a)所示,天线放置在同一个竖直平面内;当实验对象处于侧卧状态时,如图6(b)所示,天线放置在同一个水平面内。两种状态下的共同要求:使用x方向作为检测方向;天线与躯干方向平行;信号有效发射区域对准腹部的中间区域。
在实验中,
设置为30 cm,天线和腹部表面相距约为12 cm,载波频率为5.7 GHz,采样频率为50 Hz。若呼吸波形不明显,可轻微调整天线和腹部的间距,直至得到明显的呼吸波形,如图7(a)所示,两根虚线中间部分的波形反映了一次完整的呼吸过程,依次是呼吸间隔、吸气阶段、呼吸停顿、呼气阶段等,符合真实的生理过程。数据采集后,经滑动平均算法降噪处理,可得图7(b),处理窗口大小为20。
对降噪后的数据提取瞬时呼吸频率,通过实验可知,在单个呼吸周期中,CSI变化幅度基本稳定于4 dB至8 dB,因此设置呼气阶段和吸气阶段的CSI变化总阈值为3 dB,吸气阶段和呼气阶段起始位置CSI变化阈值设为1 dB,吸气阶段和呼气阶段的时长阈值为4 s,二者间距时长为1 s。以3位同学在平卧和侧卧姿势下分别持续10分钟的呼吸数据为例,三人连续100次的瞬时呼吸频率随时间推移变化如图8所示,实验人员A、B、C的呼吸频率范围依次为8~12/min、15~18/min、15~22/min,符合年轻人的呼吸频率8~24.8/min [13] 。从呼吸频率的波动性角度来看,实验人员A和B的呼吸频率波动相对比较平稳,实验人员C的呼吸频率波动则较大。从睡姿角度来看,三位实验人员的呼吸表现均符合侧卧略快于平卧。经观察可知,瞬时呼吸频率随时间推移呈现一定的波动,主要原因有3个:设备工作不稳定,所带来的部分影响难以消除;人的呼吸不均匀;瞬时呼吸频率提取算法不完善,呼吸周期分割不准确,需要改进。
WI-BD模型与其他基于WIFI信号的呼吸检测对比如表2所示,很明显本文所述模型在多个方面具有显著的优势。本文已证明天线间距显著影响有效检测范围,且不同方向上菲涅尔区半径存在差异性,因此认为本文所述模型在经过调整后可用于多人模式下呼吸检测,未来工作中将进一步予以探索。
 (a) 平卧睡姿 (b) 侧卧睡姿
(a) 平卧睡姿 (b) 侧卧睡姿
Figure 6. The Experimental arrangement of supine posture and lateral decubitus posture
图6. 平卧和侧卧睡姿下实验布置示意图
 (a) 降噪前
(a) 降噪前  (b) 降噪后
(b) 降噪后
Figure 7. De-noising treatment of respiratory data
图7. 呼吸数据的降噪处理
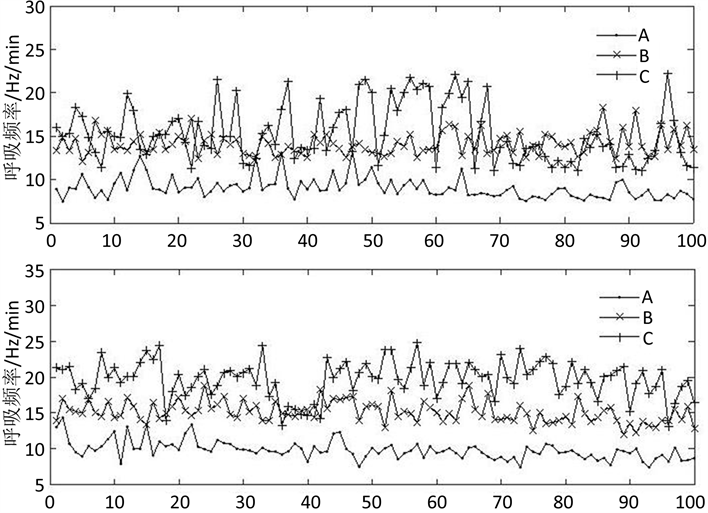
Figure 8. The change of instantaneous respiratory frequency
图8. 瞬时呼吸频率变化

Table 2. The comparison of respiratory detection models based on WIFI signal (unit: dB)
表2. 基于WIFI信号的呼吸检测模型对比(幅度:dB)
本文中所使用的实验设备和软件工具:Intel 5300网卡、2台mini PC、CSI Tool软件、MATLAB软件、18dB增益天线。
5. 结束语
本文通过数学分析方式论证菲涅尔区半径随方向的变化趋势,并结合信号传播原理和天线特征,优化天线设置方式,提出一种基于菲涅尔区的WI-BD模型,并对单目标平卧和侧卧两种睡姿下呼吸检测进行验证,实验结果符合预期。
相比文献 [1] [2] [3] [4] [8] ,本文所提出的WI-BD模型具备多个显著优点:无须预先计算天线位置,可获得最佳菲涅尔区半径;更受控的有效监控区域和更佳的抗干扰性;检测模型对空间需求显著减小,更有利于在更多场景下使用。未来的工作将基于文中所述模型,进一步完善在更多睡姿和更多目标数量下的应用。
基金项目
国家自然科学基金面上项目(61772169)。
参考文献