1. 引言
本篇文章的目的是在
上构造超Gabor框架并且研究一维空间的矩阵格变换算子。我们先介绍下关于本文的基本概念:
若 是希尔伯特空间。一个
是希尔伯特空间。一个 里的序列
称作框架,如果存在常数
,使得:
里的序列
称作框架,如果存在常数
,使得:
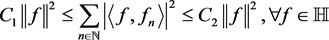
当
时,框架
叫做紧框架;当
时,框架
叫做正规紧框架。
若
和
是
中两个满秩的格。那么
中满秩的格
通常被视为可分的时频格:
作为频域格,
作为时域格 [1] 。在
情况下,序列有下面这种形式:
其中
。并且
是Gabor (或Weyl Heisenberg)族定义的由
的时频偏移获得的函数集合 [2] 。我们称
是Gabor框架生成元,当序列
是一个Gabor框架的时候。即当存在常数
使得对于全部 时,我们有
时,我们有
当
,该框架叫做Parseval Gabor框架生成元。
本文的焦点在超Gabor框架的构建以及矩阵格变换算子上,一个向量
叫做长度为L的超Gabor框架生成元,如果
是希尔伯特直和空间
上的一个框架,其中
。
在一维空间如果存在长度为L的超Gabor框架,那么
,此时
。事实上任何
Parseval框架生成元
都满足范数条件
[3] 。
2. 引理准备
一些超Gabor框架L = 1即Gabor框架时的一些引理:
引理2.1:存在前框架函数族
(当格
时),使得
以及
。
引理2.2:如果
,则存在函数
,使得
是
中的一个框架 [4] 。
引理2.3:令
和
是
中两个满秩的格,因此:
1) 存在长度为L的超Gabor框架的充要条件是
;
2) 存在长度为L的正交超Gabor框架的充要条件是
[5] 。
3. 主要结果
首先给出本文的主要结论之一如何构造一维超Gabor框架。在之前的基础上拓展到任意满秩的格
,而不是
。首先,称
是
的全数字集合如果
满足
是
的划分区间。
定理3.1:令
是满秩的格。若
是
的全数字集合,那么对于任意的
的基本域
,向量
是长度为L的超Gabor框架生成元(特别当
的时候,为一个正交超Gabor框架),其中
,
(
).
证明:首先证明
是
的一个划分区间,因此每一个
通过
为瓦格覆盖了
。由
是
的一个全数字集合,得到:
。因此
接下来证明每一个
的不相交性:如果
,那么
且
。因此
且
,其中
,
。又因为
。因此我们得到:
.
因为
是一个瓦格,所以
,并且
。这与
矛盾,因此我们得到
。
下面证明每一个
是以
为瓦格的:首先令
。记
,
,其中
,
。因此得到
。因为
是以
为瓦格的,有
,
,所以
,
,
。这样就证明了
通过
包裹
;第二,证明
。对于任意
,有一些
,
使得
。不失一般性,假设
,则
,
。这意味着
是
平移的
的同余子集。对于任意
,有一些
,使得
。由于
是
瓦格的,有
,其中
,
。这意味着
。因为
,因此
。这样就证明了
是
平移的
的同余子集。所以
是
平移的
的同余子集,即
。
是
平移的
的同余子集的证明可以在 [5] 中看到。最后我们证明
是长度为L的超Gabor框架。这就要求
是
的Parseval框架并且
和
是强不相交的。
由上可知
通过
为瓦格覆盖了
通过
包裹
。由此可得
,
,对于任意
。记
对每一个
,可得
。这样可知:
.
因此
是一个
的Parseval框架。
对于每一个l有:
,
其中
。因为
和
是
的不相交的基本域。这样得到:
,
因此
和
是强不交的 [6] 。所以
是一个长度为L的超Gabor框架。
特别的,当
时,
。所以
是一个长度为L的正交超Gabor框架。
上述定理给出了一维空间对于任何满秩的格
如何构造超Gabor框架。下个定理将给出如何在
上构造超Gabor框架的方法。首先定义一些概念:记
是
的四条边线,
是其中最短的一条。令
是
的两个端点,那么
。并且定义以下符号(
):
,
定理3.2:令
和
是满秩的格,并且
。则对
的任意基本域
,向量
是长度为L的超Gabor框架生成元(特别的当
时,是一个正交超Gabor框架),其中
并且
.
因为
并且每一个
,所以得到L个
。因此
(
,
).
这个定理可以非常简单的证明。我们可以关注以下几点:第一,
是
的划分区间;第二,每一个
是
瓦格的;最后
.
因此在这种情况下存在超Gabor框架。当
时,存在正交超Gabor
框架。下一节给出如何用定理3.1和定理3.2构造超Gabor框架的例子。接下来从格同构和矩阵格变换算子的定义开始,研究矩阵格变换算子 [7] 。
定义3.3:令
,
和
,
是
中四个满秩的格。一个超Gabor框架:
和另外一个超Gabor框架:
称为格同构的,如果
。
定义3.4:矩阵
称为超Gabor框架的矩阵格变换算子,如果
,其中A、B、C、
D如同定义3.3里一样。
一维超Gabor框架的矩阵格变换算子有一个性质。
定理3.5:对角矩阵或者反对角矩阵A是一个超Gabor框架的矩阵格变换算子当且仅当
。
证明:我们只证明对角矩阵的情形就可以,反对角矩阵同理可得。我们先证定理3.5的必要性。如果
和
是两个超Gabor框架,其中
是
中四个满秩的格 [8] 。存在一个矩阵
格变换算子,使得
。
令
,所以我们可以得到
,所以
.
由上式可得:
,
。用以上方程直接计算
。因为
,所以
。
现在证明定理3.5的充分性:如果有一个对角矩阵形如
并且满足
。存在
(
)的超Gabor框架
。则我们用A对
做变换。得到
,所以
。
那么存在
作为时频格的超Gabor框架
。
[9]
。因此A符合定义3.4,即A是一个超Gabor框架的矩阵格变换算子。
需要注意的是:如果一个矩阵A满足
,其中a、b、c、d是两个超Gabor框架的四个满秩的格。A不一定是一个矩阵格变换算子。例如:
,则存在一个矩阵
使得
并且
.,但是
。
推论3.6:对于一维超Gabor框架:
,
它一定格同构于另一个超Gabor框架:
.
并且存在一个矩阵格变换算子A使得
。
4. 算例
论文在本节给出有关如何构造超Gabor框架的例子。同时我们也使用矩阵格变换算子得到新的超Gabor框架。
例4.1:1) 令
。那么
,令
是通过
为瓦格覆盖了
的区间。令
,其中每一个
就像图1中所示。那么由定理3.1,
是长度为2的超Gabor框架。
2) 令
。那么
,令
是通过
为瓦格覆盖了
的区间。令
,其中每一个
就像图2中所示。那么由定理3.1,
是长度为2的超Gabor框架。
例4.2:1) 存在长度为6的超Gabor框架:
存在另一个长度为6的超Gabor框架:
它们的格是同构的,因为
。
2) 存在对角矩阵
是一个矩阵格变换算子,使得
并且
。上述框架可见图3和图4。
最后我们给出一些
上构造超Gabor框架的例子:
例4.3:令
,
。
,
,
。令
是
的一个瓦格。令
,其中每一个
就像图5中所示。那么由定理3.2,
长
度为2正交超Gabor框架。
例4.4:令
,
。
,
。令
是
的一个瓦格。令
,其中每一个
就像图6中所示。那么由定理3.2,
长度为9的超Gabor框架。
5. 结论
本文给出了如何构造任意满秩格的超Gabor框架。发现超Gabor框架必格同构到一个正交超Gabor框架。奇妙的是,可以采取矩阵格变换算子使它们有联系。通过构造方法可以很容易地得到一个
正交的超Gabor框架,任何超Gabor框架都可以和它是格同构的。因此,可以更好地理解超Gabor框架和正交超Gabor框架。
致谢
感谢审稿老师提出的宝贵的修改意见。感谢国家自然科学基金委的支持。
基金项目
国家自然科学基金(项目号:11571107)。