一种风电接入对两区域电网功角稳定性的影响因素的分析方法

doi:10.12677/JEE.2018.63026

期刊菜单

一种风电接入对两区域电网功角稳定性的影响因素的分析方法
An Analysis Method for the Influence Factors of Wind Power Access on the Stability of Power Angle of Two-Region Power Grid

DOI: 10.12677/JEE.2018.63026, PDF, HTML, XML,
作者: 孙应毕, 刘志坚^*, 晏永飞, 王旭辉：昆明理工大学，电力工程学院，云南昆明
关键词: 风电；功角稳定；区域电网；电磁功率特性；Wind Power； Power Angle Stability； Regional Power Grid； Power Characteristics

摘要: 本文提出了一种风电接入对两区域电网功角稳定性的影响因素的分析方法。首先将风机以负阻抗的形式接入到电力系统中；然后根据系统的潮流方程，得到两区域发电机的电磁功率特性曲线，并进一步等值为单机电磁功率；根据风电接入量和两区域同步机分配率的不同，得到两区域同步机的机械功率，并进一步等值为单机机械功率；从等值单机的角加速度的变化量出发，考虑网络拓扑结构、风电接入位置、两区域发电机转动惯量比例、两区域发电机分配率和风电接入比例对系统暂态稳定的影响。本文提出的方法可指导最优的风电接入，以使对电力系统稳定性的影响最小，并且在两区域系统仿真中验证了本文所提方法的正确性。

Abstract: This paper presents an analysis method for the influence factors of wind power access on the stability of power grids in two regions. Firstly, the fan is connected to the power system in the form of negative impedance; then according to the power flow equation of the system, the electromagnetic power characteristic curve of the two-region generator is obtained, and further equivalent to the single-machine electromagnetic power; according to the wind power access amount and the two regions and the difference of the distribution rate of the synchronous machine, the mechanical power of the two-zone synchronous machine is obtained, and the equivalent value is the mechanical power of the single machine. Starting from the variation of the angular acceleration of the equivalent single machine, the influence of the network topology, the wind power access position, the two-region power generation’s machine moment of inertia ratio, the two-zone generator distribution rate and the wind power access ratio on system transient stability are considered. The proposed method can guide the optimal wind power access to minimize the impact on the stability of the power system, and verify the correctness of the proposed method in the simulation of the two-region system.

文章引用：孙应毕, 刘志坚, 晏永飞, 王旭辉. 一种风电接入对两区域电网功角稳定性的影响因素的分析方法[J]. 电气工程, 2018, 6(3): 220-229. https://doi.org/10.12677/JEE.2018.63026

1. 引言

由于环境和经济问题逐渐成为我们社会的主要问题，因此需要在可再生能源发电方面做出更多努力。在正在开发的可再生能源技术中，风力涡轮机技术是世界上增长最快的技术。采用双馈感应发电机(DFIG)的变速风力涡轮机(VSWT)是目前安装的风力涡轮机中最流行的技术。随着DFIG风力发电机组渗透水平的不断提高，电力系统稳定性成为一个需要适当研究的重要问题。

其中，最主要的问题之一就是功角稳定性，为了指导风机的接入，我们需要分析风机接入后对系统功角稳定性影响的因素。对于现有的绝大多数技术，仅仅得出了风机接入对系统影响是好或坏的结论。但是系统的功角稳定性受到多方面的影响，因此需要综合分析，电力系统在不同的运行状态下可能风机对系统功角稳定性的影响是不一样的。

文献 [1] 推导了风电直接接入与等容量替换同步机时的系统同步机功角特性方程，并分析了风电接入比例与传输线电抗对双馈风电接入对暂态功角稳定的影响。文献 [2] 基于系统惯性中心(COI)，推导并网DFIG典型接入方式下系统COI的运动方程和COI坐标系下各同步发电机的运动方程，并结合DFIG的典型并网方式和接入条件，详细研究了并网DFIG对本地系统暂态行为的关键影响因素以及本地系统的COI和各同步发电机的暂态响应的相应变化趋势。文献 [3] 、 [4] 根据双馈风机的暂态特性，在双馈风机简化模型和直流潮流计算方法的基础上，利用扩展等面积定则分析了双馈风机接入两机系统后系统暂态功角稳定性的变化，提出一种判断风电接入对两机系统暂态功角稳定影响的判据。文献 [5] 基于双馈风电机组在故障期间的等效外特性和单端送电系统的功率特性方程，研究不同风电规模对送端电网和受端电网之间电气距离的影响，以及不同风电规模在不同故障状态下对系统暂态功角稳定性的影响机理。文献 [6] 基于扩展等面积准则(EEAC)，研究了风电比例对风火打捆交直流混联外送系统的功角暂态稳定性的影响。文献 [7] 基于双馈感应电机的风电机组进行动态模拟以及对包含风电场的实际系统的仿真计算，研究了不同风电场接入容量和系统故障情况对系统暂态稳定的影响。文献 [8] 通过分析DFIG接入对系统惯性中心运动方程中关键因素的影响，揭示了DFIG以不同方式接入系统时对系统惯性中心功角加速度暂态响应的影响机理。

风电场的大规模接入对电力系统原有的暂态稳定造成极大影响，有必要对含风电场的电力系统暂态稳定性进行理论分析研究。本文提出一种从理论上分析风电接入对多机系统暂态功角稳定性影响的方法。从风机对同步机的影响途径出发，用等效的接地导纳来反映风电场的对外功率特性，并提出将接地导纳包含的有功无功功率信息糅入同步机节点导纳矩阵中的方法，使得风电场对系统暂态功角稳定性的影响得以量化，该研究对含风电场的多机系统暂态稳定性的分析奠定了理论基础。

2. 风机等效模型

对于同步机互同步稳定而言，风电的接入可视为向多同步机互联系统中引入一个非自治因素，即风电对外输出的有功、无功功率。该因素引起系统的潮流发生变化，各同步机相连节点的节点电压幅值和相位随之改变，影响各同步机的电磁功率，从而改变整个系统内同步机功角之间的互同步性。

将风机以负阻抗的形式接入到电力系统中，其阻抗值如下：

$Y_{w} = - \frac{P_{w}}{U_{w}^{2}} + \frac{Q_{w}}{U_{w}^{2}} j$ (1)

式中 $U_{w}$ 为风机接入系统处的母线电压； $P_{w}$ 为风机的有功功率； $Q_{w}$ 为风机的无功功率；j为虚数单位。

3. 风电接入对区域电网的影响

3.1. 扩展等面积法

利用文献 [8] 的假设，扰动后的多机系统分为两群，即超前群S和滞后群A，等值双机电力系统的角度，角速度，机械功率和电磁功率如下所示：

$Δ ω_{S} = \sum_{i \in S} M_{i} Δ ω_{i} / M_{S}$

$Δ ω_{A} = \sum_{i \in A} M_{i} Δ ω_{i} / M_{A}$

$δ_{S} = \sum_{i \in S} M_{i} δ_{i} / M_{S}$

$δ_{A} = \sum_{i \in A} M_{i} δ_{i} / M_{A}$

$P_{e a} = \sum_{i \in A} P_{e i}$ , $P_{m a} = \sum_{i \in A} P_{m i}$

$P_{m s} = \sum_{i \in S} P_{m i}$ , $P_{e s} = \sum_{i \in S} P_{e i}$ (2)

进一步地，多机系统能够被等值为单机无穷大系统：

$δ = δ_{S} - δ_{A}$

$Δ ω = Δ ω_{S} - Δ ω_{A}$

$M = \frac{M_{S} M_{a}}{M_{T}}$

$Δ P = P_{M} - P_{e}$ (3)

其中

$P_{M} = \frac{M_{A} P_{m s} - M_{S} P_{m a}}{M_{T}}$ , $P_{e} = \frac{M_{A} P_{e s} - M_{S} P_{e a}}{M_{T}}$

$M_{T} = \sum M_{i}$ , $M_{A} = \sum_{i \in A} M_{i}$ , $M_{S} = \sum_{i \in S} M_{i}$

$M_{T}$ 是所有发电机组的转动惯量， $M_{A}$ 、 $M_{S}$ 分别是超前群和滞后群的总转动惯量； $P_{e s}$ 、 $P_{e s}$ 分别是超前群的等效机械功率和电磁功率； $P_{m a}$ 、 $P_{e a}$ 分别是滞后群的等效机械功率和电磁功率。M为单机等值转动惯量。

3.2. 风电接入对功率特性曲线的影响途径

根据非自治非线性多刚体系统稳定性分析理论，假设系统内共有n台同步机，所有同步机可以划分为两个机群，超前群S和余下群A，其中设S机群同步机数量为p。考虑同步机的内电势节点，将系统内所有节点分成四类，分别是S群同步机内电势节点和A群同步机内电势节点，风电出口节点W和网络中普通功率交换节点R。

系统的节点电压方程为：

$[\begin{array}{l} Y_{S S} Y_{S R} Y_{S W} Y_{S A} \\ Y_{R S} Y_{R R} Y_{R W} Y_{R A} \\ Y_{W S} Y_{W R} Y_{W W} Y_{W A} \\ Y_{A S} Y_{A R} Y_{A W} Y_{A A} \end{array}] [\begin{array}{l} E_{S} \\ E_{R} \\ U_{W} \\ U_{A} \end{array}] = [\begin{array}{l} I_{S} \\ I_{R} \\ 0 \\ 0 \end{array}]$ (4)

对节点电压方程进行第一步化简：

$[\begin{array}{l} Y_{S S} Y_{S R} Y_{S W} \\ Y_{R S} Y_{R R} Y_{R W} \\ Y_{W S} Y_{W R} Y_{W W} \end{array}] [\begin{array}{l} E_{S} \\ E_{R} \\ U_{W} \end{array}] + [\begin{array}{l} Y_{S A} \\ Y_{R A} \\ Y_{W A} \end{array}] \frac{1}{Y_{A A}} {[\begin{array}{l} Y_{A S} \\ Y_{R A} \\ Y_{A W} \end{array}]}^{T} [\begin{array}{l} E_{S} \\ E_{R} \\ U_{W} \end{array}] = [\begin{array}{l} I_{S} \\ I_{R} \\ 0 \end{array}]$ (5)

对节点电压方程进行第二步化简：

$\begin{array}{l} [\begin{array}{l} Y_{S S} + \frac{Y_{S A} Y_{A S}}{Y_{A A}}, Y_{S R} + \frac{Y_{S A} Y_{R A}}{Y_{A A}} \\ Y_{R S} + \frac{Y_{R A} Y_{A S}}{Y_{A A}}, Y_{R R} + \frac{Y_{R A} Y_{R A}}{Y_{A A}} \end{array}] [\begin{array}{l} E_{S} \\ E_{R} \\ U_{W} \end{array}] \\ + [\begin{array}{l} Y_{S W} + \frac{Y_{S A} Y_{A W}}{Y_{A A}} \\ Y_{R W} + \frac{Y_{R A} Y_{A W}}{Y_{A A}} \end{array}] \frac{1}{Y_{W W} + \frac{Y_{W A} Y_{A W}}{Y_{A A}}} {[\begin{array}{l} Y_{S W} + \frac{Y_{S A} Y_{A W}}{Y_{A A}} \\ Y_{R W} + \frac{Y_{R A} Y_{A W}}{Y_{A A}} \end{array}]}^{T} [\begin{array}{l} E_{S} \\ E_{R} \\ U_{W} \end{array}] = [\begin{array}{l} I_{S} \\ I_{R} \\ 0 \end{array}] \end{array}$ (6)

对节点电压方程进行第三步化简：

$[\begin{array}{l} Y_{S S 1}, Y_{S R 1} \\ Y_{R S 1}, Y_{R R 1} \end{array}] [\begin{array}{l} E_{S} \\ E_{R} \end{array}] = [\begin{array}{l} I_{S} \\ I_{R} \end{array}]$ (7)

式中

${\begin{cases} Y_{S S 1} = Y_{S S} + \frac{Y_{S A} Y_{S A}}{Y_{A A}} + \frac{(Y_{S W} + \frac{Y_{S A} Y_{A W}}{Y_{A A}}) (Y_{W S} + \frac{Y_{W A} Y_{S A}}{Y_{A A}})}{Y_{W W} + \frac{Y_{W A} Y_{A W}}{Y_{A A}}} \\ Y_{S R 1} = Y_{S R} + \frac{Y_{S A} Y_{R A}}{Y_{A A}} + \frac{(Y_{S W} + \frac{Y_{S A} Y_{A W}}{Y_{A A}}) (Y_{R W} + \frac{Y_{R A} Y_{A W}}{Y_{A A}})}{Y_{W W} + \frac{Y_{W A} Y_{A W}}{Y_{A A}}} \\ Y_{R S 1} = Y_{R S} + \frac{Y_{R A} Y_{S A}}{Y_{A A}} + \frac{(Y_{R W} + \frac{Y_{R A} Y_{A W}}{Y_{A A}}) (Y_{S W} + \frac{Y_{S A} Y_{A W}}{Y_{A A}})}{Y_{W W} + \frac{Y_{W A} Y_{A W}}{Y_{A A}}} \\ Y_{R R 1} = Y_{R R} + \frac{Y_{R A} Y_{A A}}{Y_{A A}} + \frac{(Y_{R W} + \frac{Y_{R A} Y_{A W}}{Y_{A A}}) (Y_{R W} + \frac{Y_{R A} Y_{A W}}{Y_{A A}})}{Y_{W W} + \frac{Y_{W A} Y_{A W}}{Y_{A A}}} \end{cases}$

由式(5)和(6)可知，W节点也不是简单被去除，而是将W节点包含的风机有功和无功信息糅入到同步机节点的导纳矩阵中，即将风电对同步机电磁功率的影响转化为对同步机之间电气联系强弱的改变。由节点注入电流公式可计算出各同步机的电磁功率，以S机群中第i台同步机为例。

1) 建立两区域发电机功率特性曲线：

${\begin{cases} P_{e S 1} = P_{e S} + Δ P_{e S} = E_{S}^{2} (G_{S S} + Δ G_{S S}) + E_{S} E_{R} (B_{S R} + Δ B_{S R}) \sin δ_{S R} + E_{S} E_{R} (G_{S R} + Δ G_{S R}) \cos δ_{S R} \\ P_{e R 1} = P_{e R} + Δ P_{e R} = E_{R}^{2} (G_{R R} + Δ G_{R R}) + E_{S} E_{R} (B_{R S} + Δ B_{R S}) \sin δ_{S R} + E_{S} E_{R} (G_{R S} + Δ G_{R S}) \cos δ_{S R} \end{cases}$ (8)

建立等值单机功率特性曲线：

$P_{e 1} = \frac{M_{R} P_{e S 1} - M_{S} P_{e R 1}}{M_{S} + M_{R}} = (P_{e} + Δ P_{e}) + (P_{\max} + Δ P_{\max}) \sin (δ_{S R} - r + Δ r)$ (9)

式中

${\begin{cases} Δ P_{c} = \frac{M_{R} E_{S}^{2} Δ G_{S S} - E_{R}^{2} M_{S} Δ G_{R R}}{M_{S} + M_{R}} = (1 - a_{M}) E_{S}^{2} Δ G_{S S} - a_{M} E_{R}^{2} Δ G_{R R} \\ P_{e} = \frac{M_{R} E_{S}^{2} G_{S S} - E_{R}^{2} M_{S} G_{R R}}{M_{S} + M_{R}} \\ P_{\max} + Δ P_{\max} = \sqrt{{(E_{S} E_{R} (B_{S R} + Δ B_{S R}))}^{2} + {(E_{S} E_{R} (G_{S R} + Δ G_{S R}))}^{2}} \\ r + Δ r = \arctan (\frac{E_{S} E_{R} (G_{S R} + Δ G_{S R})}{E_{S} E_{R} (B_{S R} + Δ B_{S R})}) \end{cases}$

式中 $E_{S}$ 为区域S发电机所连节点S处的电压； $E_{R}$ 为区域R发电机所连节点R处的电压； $U_{W}$ 为网络节点W处的电压； $U_{A}$ 为网络节点A处的电压； $I_{S}$ 为为区域S发电机所连节点处注入的电流； $I_{R}$ 为区域R发电机所连节点处注入的电流； $Y_{S S}$ 为节点S的自导纳； $Y_{S R}$ 为节点S、R的互导纳； $Y_{S W}$ 为节点S、W的互导纳； $Y_{S A}$ 为节点S、A的互导纳； $Y_{R S}$ 为节点R、S的互导纳； $Y_{R R}$ 为节点R的自导纳； $Y_{R W}$ 为节点R、W的互导纳； $Y_{R A}$ 为节点R、A的互导纳； $Y_{W S}$ 为节点W、S的互导纳； $Y_{W R}$ 为节点W、R的互导纳； $Y_{W W}$ 为节点W的自导纳； $Y_{W A}$ 为节点W、A的互导纳； $Y_{A S}$ 为节点A、S的互导纳； $Y_{A R}$ 为节点A、R的互导纳； $Y_{A W}$ 为节点A、W的互导纳； $Y_{A A}$ 为节点A的自导纳； $P_{e S 1}$ 为风电接入后区域S发电机的电磁功率； $P_{e S}$ 为风电接入前区域S发电机的电磁功率； $Δ P_{e S}$ 为风电接入后引起的区域S发电机的电磁功率改变量； $P_{e R 1}$ 为风电接入后区域R发电机的电磁功率； $P_{e R}$ 为风电接入前区域R发电机的电磁功率； $Δ P_{e R}$ 为风电接入后引起的区域R发电机的电磁功率改变量； $(G_{S S} + Δ G_{S S})$ 为 $Y_{S S 1}$ 的实部； $(B_{S R} + Δ B_{S R})$ 为 $Y_{S R 1}$ 的虚部； $(G_{S R} + Δ G_{S R})$ 为 $Y_{S R 1}$ 的实部； $(G_{R R} + Δ G_{R R})$ 为 $Y_{R R 1}$ 的实部； $(B_{R S} + Δ B_{R S})$ 为 $Y_{R S 1}$ 的虚部； $(G_{R S} + Δ G_{R S})$ 为 $Y_{R S 1}$ 的实部； $δ_{S R}$ 为区域S发电机与区域R发电机的功角差； $M_{S}$ 为区域S发电机的转动惯量； $M_{R}$ 为区域R发电机的转动惯量； $P_{e 1}$ 为风电接入后等值为单机后的电磁功率。

2) 建立两区域发电机的等值机械功率

由于风电接入有功功率为 $P_{w}$ ，假设区域S发电机的分配率为 $β$ ，则区域R发电机的分配率为 $(1 - β)$ ，则两区域发电机的机械功率如下：

${\begin{cases} P_{m S 1} = P_{m S} - β P_{w} \\ P_{m R 1} = P_{R S} - (1 - β) P_{w} \end{cases}$ (10)

等值单机机械功率：

$\begin{matrix} P_{m 1} = P_{m} + Δ P_{m} = \frac{M_{R} (P_{m S} - β P_{w}) - M_{S} (P_{m R} - (1 - β) P_{w})}{M_{S} + M_{R}} \\ = \frac{M_{R} P_{m S} - M_{S} P_{m R}}{M_{S} + M_{R}} + \frac{- M_{R} β P_{w} + M_{S} (1 - β) P_{w}}{M_{S} + M_{R}} \\ = (1 - a_{M}) P_{m S} - a_{M} P_{m R} + (a_{M} - β) P_{w} \end{matrix}$ (11)

式中

$Δ P_{m} = \frac{- M_{R} β P_{w} + M_{S} (1 - β) P_{w}}{M_{S} + M_{R}} = (a_{M} - β) P_{w}$

$P_{m S 1}$ 为风电接入后区域S发电机的机械功率； $P_{m S}$ 为风电接入前区域S发电机的机械功率； $P_{m R 1}$ 为风电接入后区域R发电机的机械功率； $P_{R S}$ 为风电接入前区域R发电机的机械功率； $P_{w}$ 为风机的有功功率； $β$ 为区域S发电机的分配率为； $P_{m 1}$ 为风电接入后等值为单机后的机械功率； $P_{m}$ 为风电接入前等值单

机的机械功率； $Δ P_{m}$ 为风电接入后引起的等值单机的机械功率改变量； $a_{M} = \frac{M_{S}}{M_{S} + M_{R}}$ 。

3) 风电接入后等值单机的角加速度的变化量

考虑等值单机的电磁功率幅值和相位的变化对系统的功角稳定性不影响；则

$\begin{matrix} f = {\overset{''}{δ}}_{1} - \overset{''}{δ} = \frac{1}{T} (P_{m 1} - P_{e 1}) - \frac{1}{T} (P_{m} - P_{e}) = \frac{1}{T} (Δ P_{m} - Δ P_{e}) \\ = \frac{1}{T} ((a_{M} - β) P_{w} - (1 - a_{M}) E_{S}^{2} Δ G_{S S} + a_{M} E_{R}^{2} Δ G_{R R}) \end{matrix}$ (12)

f风电接入前后等值单机的角加速度的变化量； ${\overset{''}{δ}}_{1}$ 为风电接入后的发电机角加速度； $\overset{''}{δ}$ 为风电接入前的发电机角加速度； $P_{m 1}$ 为风电接入后的等值机械功率； $P_{e 1}$ 为风电接入后的等值电磁功率；T为等

值转动惯量， $T = \frac{M_{S} M_{R}}{M_{S} + M_{R}}$ 。

3.3. 风电接入对区域电网的影响因素分析

网络拓扑结构的不同，则 $Y_{S S 1}$ 、 $Y_{S R 1}$ 、 $Y_{R S 1}$ 和 $Y_{R R 1}$ 也发生改变，从而影响 $Δ G_{S S}$ 和 $Δ G_{R R}$ 。根据式(12)，从而对风电接入前后对系统的功角稳定性影响也不同。

转动惯量的不同，则 $a_{M}$ 也发生改变，根据式(12)，从而对风电接入前后对系统的功角稳定性影响也不同。

风电接入位置的不同， $Y_{W W}$ 也不同，从而影响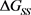和 $Δ G_{R R}$ 。根据式(12)，从而对风电接入前后对系统的功角稳定性影响也不同。

两区域发电机分配率的不同，则 $β$ 也不同，根据式(12)，从而对风电接入前后对系统的功角稳定性影响也不同。

风电接入比例的不同，则 $P_{w}$ 也不同，根据式(12)，从而对风电接入前后对系统的功角稳定性影响也不同。

4. 仿真论证

在PSD电力系统分析软件中搭建仿真模型，如图1所示。接入风机前G1出力为30 MW，G2出力为220 MW，负荷L7为150 MW，L5为100 MW，从区域2到区域1的联络线潮流约为120 MW。

案例1：考虑在节点9集中接入150 MW的风电，考虑三相接地短路故障，发生在节点6和7之间线路的50%处，故障时长为6周波。情景1是5、6节点和6、7节点为双回线；情景二为5、6节点和6、7节点为单回线，考虑系统网络拓扑结构对风电接入前后对系统的功角稳定性影响。得到的系统功角曲线如图2所示。

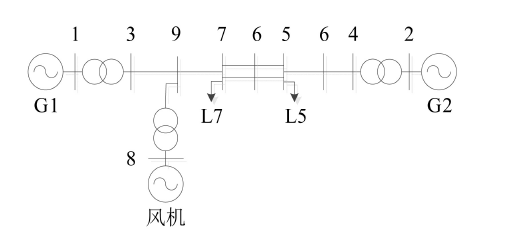
Figure 1. Extended two-machine system simulation diagram

图1. 扩展双机系统仿真示意图

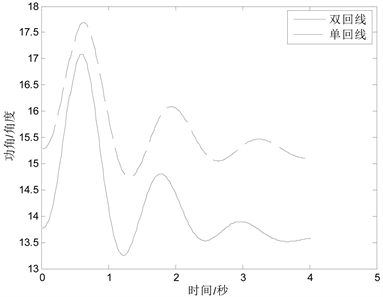
Figure 2. Generator power angle graph under different network topologies

图2. 不同网络拓扑结构下的发电机功角曲线图

案例2：考虑在节点9集中接入150 MW的风电。设置三相接地短路故障，发生在节点6和7之间线路的50%处，故障时长为6周波。情景1是风电接入到节点9；情景二为风电接入到节点6，考虑风电接入位置对风电接入前后对系统的功角稳定性影响。得到的系统功角曲线如图3所示。

案例3：考虑在节点9集中接入150 MW的风电。考虑三相接地短路故障，发生在节点6和7之间线路的50%处，故障时长为6周波。情景1为 $β = 0$ ；情景二为 $β = 0.3$ ，考虑两区域发电机分配率对系统的功角稳定性影响。得到的系统功角曲线如图4所示。

案例4：发生在节点6和7之间线路的50%处，故障时长为6周波。情景1为在节点9集中接入100 MW的风电；情景二在节点6集中接入150 MW的风电，考虑风电接入比例对系统的功角稳定性影响。得到的系统功角曲线如图5所示。

Figure 3. Fan power angle graph of generator connected to different nodes

图3. 风机接入不同节点下的发电机功角曲线图

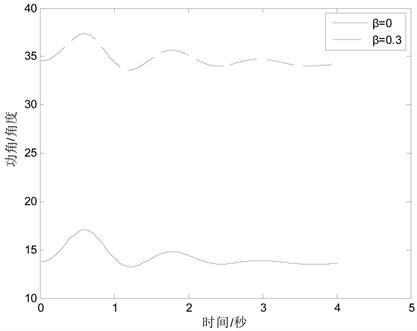
Figure 4. Generator power angle graph under different distribution rates

图4. 不同分配率下的发电机功角曲线图

案例5：考虑在节点9集中接入150 MW的风电。设置三相接地短路故障，发生在节点6和7之间线路的50%处，故障时长为6周波。情景1是 $M_{S} = 2364, M_{R} = 2364$ ；情景二为 $M_{S} = 2364, M_{R} = 1000$ ，考虑转动惯量( $a_{M}$ )对风电接入后对系统的功角稳定性影响影响。得到的系统功角曲线如图6所示。

5. 结论

本文提出一种分析含风电的电力系统暂态功角稳定性的方法，通过理论分析与仿真验证，得到如下结论：

1) 风电通过向电网输送有功功率、无功功率与同步发电机组进行电气交互，从而影响同步发电机组之间的互同步稳定性。

Figure 5. Generator power angle curve under different wind power ratios

图5. 不同风电比例下的发电机功角曲线图

Figure 6. Generator power angle curve under different moments of inertia

图6. 不同转动惯量比例下的发电机功角曲线图

2) 将风电对外功率特性用阻抗的形式表示，通过将接地导纳所包含的有功无功信息糅入同步机节点导纳矩阵，使得同步机的电磁功率特性和机械功率特性发生改变，从而影响系统的暂态稳定性。

3) 从等值单机的角加速度的变化量出发，网络拓扑结构、风电接入位置、两区域发电机转动惯量比例、两区域发电机分配率和风电接入比例均会对系统暂态稳定的产生影响。

NOTES

^*通讯作者。

参考文献

[1]	王清, 薛安成, 郑元杰, 等. 双馈型风电集中接入对暂态功角稳定的影响分析[J]. 电网技术, 2016, 40(3): 875-881.
[2]	刘斯伟. 并网双馈风电机组对电力系统暂态稳定性的影响机理研究[D]: [博士学位论文]. 北京: 华北电力大学(北京), 2016.
[3]	汤蕾, 沈沉, 张雪敏. 大规模风电集中接入对电力系统暂态功角稳定性的影响(一): 理论基础[J]. 中国电机工程学报, 2015, 35(15): 3832-3842.
[4]	汤蕾, 沈沉, 张雪敏. 大规模风电集中接入对电力系统暂态功角稳定性的影响(二): 影响因素分析[J]. 中国电机工程学报, 2015, 35(16): 4043-4051.
[5]	牟澎涛, 赵冬梅, 王嘉成. 大规模风电接入对系统功角稳定影响的机理分析[J]. 中国电机工程学报, 2017, 37(5): 1324-1332.
[6]	汤奕, 赵丽莉, 郭小江. 风电比例对风火打捆外送系统功角暂态稳定性影响[J]. 电力系统自动化, 2013, 37(20): 34-40.
[7]	于辉, 周成, 刘鲁宁. 基于DFIG的风电接入系统对电力系统暂态稳定性的影响[J]. 沈阳工程学院学报(自然科学版), 2009, 5(4): 305-307.
[8]	刘斯伟, 李庚银, 周明. 双馈风电机组对接入区域系统暂态功角稳定性的影响分析[J]. 电力系统保护与控制, 2016, 44(6): 56-61.

友情链接