基于CFD静压气体轴承的仿真分析

Simulation Analysis of Static Pressure Gas Bearing Based on CFD

摘要: 利用CFD流体计算软件对气体静压轴承三维内部流场进行数值模拟与分析。在计算中采用了湍流(Realizable K-ε)计算模型，利用计算结果对气体静压轴承的性能进行分析，得出了承载力随着转速的增加而明显的变大；在节流孔附近湍流效果明显，远离节流孔流场逐渐恢复层流；同时通过对节流小孔附近的截面的压力和马赫数分析，得出了在节流孔附近存在着超音速现象，对轴承的稳定性有一定影响，并且通过节流孔附近的压力分布以及承载力与转速的关系，得出了转速对静压轴承的静特性影响不可忽略。

Abstract: The 3-D internal flow field of aerostatic bearing is numerically simulated and analyzed by using CFD fluid calculation software. In the calculation, the calculation model of turbulence (Realizable K-ε) is used. The calculation results are used to analyze the performance of the static pressure bearing of the gas. It is concluded that the bearing capacity increases obviously with the increase of the speed. The turbulent effect near the throttle hole is obvious, and the flow field away from the throttle hole is gradually restored to the laminar flow. At the same time, the pressure and Maher number of the section near the throttle hole are analyzed, and the results are obtained. The supersonic phenomenon exists near the throttle hole, which has a certain influence on the stability of the bearing, and through the pressure distribution near the throttle hole and the relationship between the bearing capacity and the speed, the influence of the speed on the static characteristics of the static pressure bearing can not be ignored.

1. 前言

气体轴承是一种以气体为润滑介质的轴承，由供气压力使气体轴承旋转部分和静止部分分离，实现了摩擦系数较小，转速高，无污染等特征。同时随着计算机的发展和软件的不断更新，对气体轴承的分析已经不同与以往繁琐的程序编译计算，现在通过CFD流体计算软件对气体轴承进行模拟分析已经越来越方便和普遍 [1] [2] 。

对静压气体轴承的CFD研究目前都是处于对轴承的承载性以及压力分布大小进行研究；于贺春 [3] 通过CFD分析了承载力与偏心的变化关系，利用转速对轴承的影响分析了转速与承载力的变化情况，同时黄首峰 [4] 利用FLUENT对滑动轴承的油膜压力和承载特性进行了分析。郑茂建 [5] 通过CFD计算软件为基础，对不同结构的静压气体轴承的回转精度进行了系统的分析；饶河清 [6] 和孙雅洲 [7] 对多孔介质的静压气体轴承仿真，得出了多孔介质气体轴承的静特性性能。同时对于气体的可压缩性，以及流场内部的变化情况，Mori [8] 和龙威 [9] [10] 通过对止推轴承节流孔附近的流场变化情况，分析了流场区域内的冲击波；同时李运堂 [11] 通过大涡模拟分析了止推轴承的振动特性。

本文将采用三维建模方法，对模型进行有限元计算，通过求解Naver-Stokes方程，创新性地结合了压力以及马赫数的分布规律来分析气体静压轴承的静特性和节流孔附近的流场变化情况。

2. 基本方程

由Navier–Stokes方程推导出质量方程，动量方程以及能量方程适合在可压缩，稳态计算流体中：

$\frac{\partial p}{\partial x_i}\left(\rho u_i\right)=0$ (1)

$\frac{\partial p}{\partial x_i}\left(\rho u_i{u}_j\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial {\tau }_{ij}}{\partial x_j}$ (2)

方程(1)是质量守恒方程，(2)是动量守恒方程，其中u_ij是代表在笛卡尔坐标系中的速度方向，x_i和x_j是代表在坐标系中的方向向量，δ_ij是粘性应力张量。

$\frac{\partial p}{\partial x_i}\left(\rho h{u}_i\right)=\frac{\partial \left(p{u}_i\right)}{\partial x_i}+{\tau }_{ij}\frac{\partial u_i}{\partial x_j}$ (3)

(3)是能量守恒方程

${\tau }_{ij}=\left[\eta \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\right]-\frac{2}{3}\eta \frac{\partial u_i}{\partial x_i}{\delta }_{ij}$ (4)

运用质量守恒方程和能量守恒方程，可以有效保证在气膜内部的质量平衡，这是研究物理性质的基本定律，同时利用守恒方程可以有效的使计算结果的平滑性和连续性，由于超音速在计算过程中会出现振荡现象，所以运用守恒方程对分析超音速等冲击波有较好的结果。

3. 建立模型

基本结构参数，轴承直径D = 30 mm，长度L = 30 mm，气膜厚度h = 20 μm，节流孔到轴承两端距离l = 7.5 mm，节流孔直径d₀ = 0.2 mm，截流腔直径d₁ = 0.8 mm，深度h₁ = 0.1 mm，利用Gambit建立气体轴承流体区域的三维模型，如图1所示，同时通过自定设置偏心率，其中偏心是沿着90˚节流孔方向，建立不同偏心率下的气体轴承模型，通过建立不同偏心率的气体轴承流体域的三维模型进行数值模拟计算分析。

4. 网格划分

在模型建立完后对模型进行网格划分，由于气膜区域内的间隙很小，同时轴承是属于旋转体，所以整个网格的扭曲率较大；同时由于在气膜区域的结构变化较大，因此导致流场变化也很大，为了整体达到比较好的网格质量和FLUENT求解计算中更加容易收敛，需要在流速变化较大的区域进行网格划分时进行网格加密，如图2(a)中，对流速变化较大的小孔节流区域需要进行局部网格加密，同时对模型需要进行分块划分网格划分处理，将模型分为10个主要区域如图2(b)，使远离节流孔处的区域能划出规则的八面体网格。

Figure 1. The model of gas basin and the position of throttle hole

图1. 气体流域模型及节流孔位置

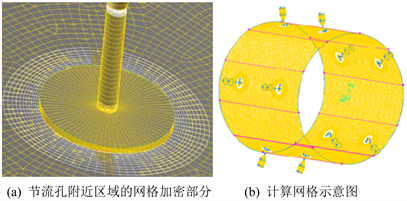
Figure 2. Schematic diagram of a computational fluid region

图2. 计算流体区域示意图

5. 边界条件及初始化

将设定进气压力边界条件(pressure-inlet)和进口边界条件(pressure-out)，压力进口边界设定在每个进气孔的外表面，压力出口边界条件为气体轴承轴向方向两端的气膜间隙面，同时定义气膜区域内的表面为壁面(wall)。

6. 求解计算

采用湍流模式(Realizable K-ε)进行湍流计算分析，稳态计算中，选用SIMPIE进行压力速度耦合计算，利用能量方程，速度方程，湍流耗散率方程进行耦合求解计算，在计算过程用为了获得更好精度的计算结构，采用二阶迎风格式，二阶迎风格式是利用了有界中心差分法进行计算。

对于CFD分析静压气体轴承分为三步，第一步是利用Gambit进行模型建立以及网格的划分，第二步利用FLUENT求解器求解计算；第三步是对求解的计算结果进行后处理分析。在计算的过程中，设立进口压力为6个大气压，压力出口边界条件为1个大气压，设立常温为工作温度。空气粘度系数为1.84 × 10⁻⁵ η(pa∙s)

7. 计算结果分析

图3是稳态湍流模拟(Realizable K-ε)在偏心率ε = 0.3，在圆周方向90˚处压力、马赫数分布图和流线图，图3(a)是压力分布图和流线图，发现在小孔深度方向气体是属于层流状态，在小孔与气膜连接处的环形区域内存在明显的回流现象，所以存在湍流的作用，同时可以看出在小孔附近的回旋比较明显，在远离小孔的方向上回旋现象逐渐衰减，最后在连接气膜区域的地方逐渐变成层流的趋势，说明了气体轴承流场的回旋的主要区域是小孔节流的环形区域，同时在小孔节流附近出现了压力减小的现象，而这种现象对气体轴承的稳定和承载性有很大的影响，图3(b)是在小孔节流处的马赫数和流线的变化情况，马赫数变化可以直接影响激波的产生和衰减，从图中可以看出在小孔附近的区域变化较为明显，同时靠近下壁面区域的马赫数变化尤为显著，而马赫数的变化情况主要取决于速度梯度的变化。

图4是稳态湍流模拟(Realizable K-ε)在圆周306˚位置处偏心率ε = 0.3时，节流孔附近的压力图，马赫数图以及流线图，在图中可以看出压力和马赫数分布与图3大致一样，在小孔内部和远离环形区域仍然是属于层流的流线状态，在环形区域内发生复杂的回旋现象，同时在可以看出在环形腔内的流线与图3相比有了很大的变化，在环形区域边缘的流线回旋变大，出现了大漩涡的现象，而且漩涡主要是分布在环形区域的上表面，与图3相比，气膜区域内整体压力减小，同时在节流孔附近减小得较为明显，在图4(b)中的马赫数变化情况也发生了较大的变化，马赫数变化范围变大，同时大于1，说明在气膜间隙较大的小孔节流处附近气体的流速变化较大，产生了超音速现象，这个变化主要出现在靠近旋转面的一边，远离于轴承的上表面区域，这主要是因为这个位置的节流孔是偏心远离的位置，导致了气膜间隙变大，由于气膜间隙变大，气体在间隙的流阻变小，则气体在节流口处的扩张速率变大。

图5是通过CFD计算得到的静压气体轴承的承载力在不同的转速，不同偏心率的情况下的承载力变化图，从图中可以看出，随着转速的不断增加，静压气体轴承的承载力是不断增加，对于高转下静压气体轴承相对于无转速的静压气体轴承，其承载力有明显的不同，因此在分析静压气体轴承时转速对其影响是不可能忽略的。

图6是不同偏心率下纯静压和转速为100,000 rpm小孔节流处的压力分布，从图中可以明显的看出，随着偏心率和转速的变大，压力分布出现了分布不均匀的现象，以90˚为对称轴，压力在两边出现了一边凸出，一边凹陷的分布，导致了压力分布不平衡，这种原因是因为气体有一定的粘性，会产生一定的挤压现象，而这种挤压现象就是静压气体轴承的动压效应。霍彩娇 [12] 通过研究名义间隙和供气压力等对轴承动态特性的影响，得出了多孔质轴承动压效应与本文结果相近，也证明了本文结果的准确性。为此在考虑静压气体轴承的稳定性时，不能仅仅只考虑静特性，应该考虑转速对静压轴承静特性的影响。

Figure 3. Eccentricity (ε = 0.3) position distribution at 90˚

图3. 偏心率(ε = 0.3)位置分布在90˚

Figure 4. Eccentricity (ε = 0.3) position distribution at 306˚

图4. 偏心率(ε = 0.3)位置分布在306˚

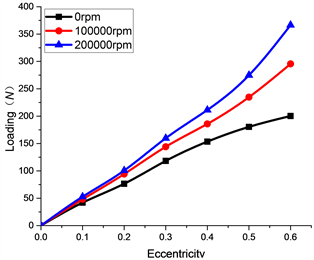
Figure 5. The change of bearing capacity with the speed

图5. 承载力随着转速的变化情况

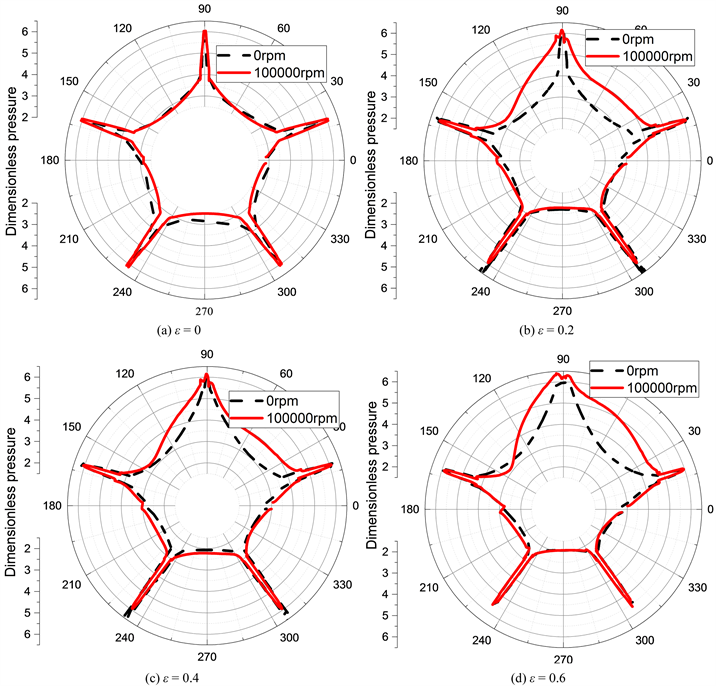
Figure 6. Interface pressure distribution diagram of the throttle hole

图6. 节流孔界面压力分布图

8. 结论

本文通过建立静压气体轴承模型，利用CFD计算软件进行仿真数值模拟计算，分析静压气体轴承节流孔附近区域以及转速对静压气体轴承的影响，通过对计算结果分析可以得到如下结论：

1) 在静压气体轴承的节流孔附近的节流腔中存在着明显的回流现象，导致了在节流孔附近的压力出现不稳定，也因此对节流腔附近的马赫数影响较大。

2) 通过不同位置处的节流孔附近的压力和马赫数对比发现，在远离偏心方向，气膜厚度增大处的马赫数较大，从而产生了超音速的马赫数，因此在节流孔附近容易产生冲击波，对轴承的稳定性有影响。

3) 在节流腔附近存在湍流，随着远离节流孔，气体在流场内逐渐恢复层流状态。

4) 随着转速的提高，气体静压轴承的承载力也逐渐变大。

5) 节流孔附近的压力随着转速的提高和偏心率的变大，气体轴承内部的挤压现象越明显，因此不能忽视转速对静压轴承静特性的影响。

基金项目

国家自然科学基金(11562002)，广西自然基金项目(2015GXNSFAA139262)，广西研究生创新项目(GKYC201704)。