1. 引言
金属氧化物避雷器(Metal Oxide Surge Arrester,简记为MOA)以其优异的非线性特性和大通流容量等优点,成为电力系统过电压保护的主要设备 [1] ,能有效抑制电力系统中的操作过电压和大气过电压。在运行电压下,MOA泄漏电流的阻性基波分量表征避雷器的功耗大小,其数值大小不受规程规定范围内的谐波电压影响 [2] ,是判别MOA运行状态的重要特征参量 [3] 。目前测量避雷器阻性电流的方法有:基波法、谐波分析法及电容电流补偿法等 [4] ,这些方法都不可避免会受到相间耦合电容的影响。此外,现有文献在消除相间干扰时,都需要测量电网电压 [5] [6] ,电压信号相位不稳定会对相间干扰的消除产生产生不利影响 [7] 。
考虑到阻性基波分量在泄漏电流中的含量较低,其数值变化对泄漏电流的数值影响很小,但对泄漏电流角度的影响很大,基于高压输电网电压幅值及相位基本不变的情况,本文利用矢量合成的原理,将三相泄漏总电流进行矢量合成,能有效去除相间耦合电容的影响;并通过合成矢量的相角变化,间接反映出单相阻性电流的增长率。
2. 数学模型
电力系统中三相避雷器一般按“一”字排列,由于A、C两相相隔较远,可忽略它们之间的相间耦合电容的影响 [8] ,只考虑A、B和B、C之间的相间耦合电容,三相避雷器工作时的等效电路如图1所示。
其中
、
、
分别是A、B、C三相避雷器阀片等效电容,
、
、
分别是A、B、C三相避雷器阀片等效非线性电阻,
是相间等效电容。
根据交流电的旋转矢量定义,由图1中电流间关系能得到式(1)如下:
(1)
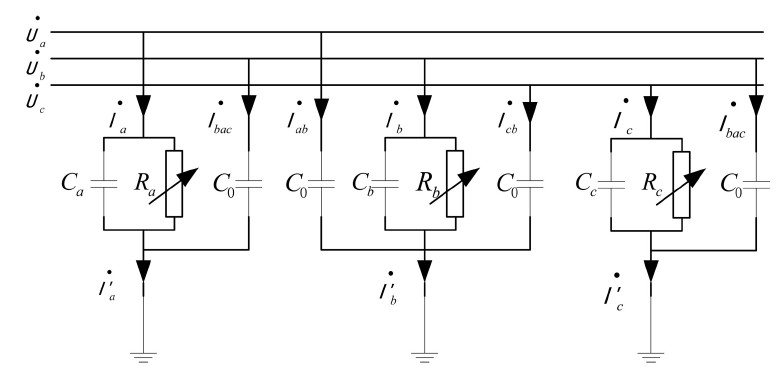
Figure 1. Equivalent circuit of three-phase MOA
图1. 三相MOA等效电路
式中
、
、
分别是电网三相电压基波矢量,
、
、
是A、B、C三相避雷器阀片基波电流矢量,
、
、
是A、B、C三相避雷器底部电流矢量,
、
分别是
、
通过耦合电容作用到B相的电流矢量,
是
通过耦合电容作用到A、C相上的电流矢量。
根据式(1),能得到如图2所示的三相MOA泄漏电流基波矢量图。
从图2中可以看出,在幅值方面,三相的泄漏电流幅值所受的影响都不大;而在相角方面,B相电流相位基本不变,A、C相电流受耦合电容电流影响,相位变化较大。
3. 阻性基波电流对总泄漏电流基波幅值和相位的影响
设流过该相阀片的电流矢量与其参考电压矢量之间夹角为
,电流矢量的幅度为
,那么其阻性电流
的幅值则为
,容性电流
的幅值为
。当阻性电流增幅为k%时,流过该阀片的泄漏电流为
,流过该相阀片的电流矢量与该相的参考电压矢量之间的夹角变为
。由于阻性基波电流在总泄露电流中的占比一般为10%~20%,其增长变化对总泄露电
流角度的影响远远大于对总泄露电路幅值的影响。
以典型MOA参数为例,假设泄漏电流基波有效值为0.4 mA,电流基波与电压基波夹角为85˚,表1所示为阻性基波电流从增大10%到增大100%后,总泄露电流相角与幅值的变化率。
从表1可得,当阻性电流增大100%,总泄漏电流的幅值增加0.0045 mA,变化率为1.13%,而泄漏电流的相角减小5˚,其变化率为5.88%。不论从绝对精度还是相对变化率上,都可以发现,能更容易从相角变化来判断阻性基波电流的变化。
4. 耦合电容对总泄漏电流幅值和相角的影响
耦合电容对泄露电流的幅值和角度都有影响,尤其是对角度的影响,严重干扰阻性基波电流的测量。以上述典型MOA参数为例,泄漏电流基波有效值为0.4 mA,阻性电流基波与电压基波夹角为85˚,表2所示为
的有效值从0.01 mA到0.08 mA后,耦合电容对总泄漏电流幅值和相角的变化率。
表中ΔA、ΔB和ΔC分别为A、B、C三相MOA在不同耦合电流影响下,三相泄漏总电流的相角影响。
从表2中我们可以看出,耦合电容对泄漏总电流相角影响远大于对其幅值的影响,那么去除耦合电容就显得尤为重要。

Figure 2. Three-phase MOA leakage current fundamental vector illustration
图2. 三相MOA泄露电流基波矢量图

Table 1. Resistive current increases by 100%, the magnitude of the leakage current and the rate of change of phase angle
表1. 阻性电流增大100%,泄漏电流的幅值和相角的变化率
5. 合成矢量
根据式(1),构造如下合成矢量:
(2)
式中
、
、
是三相阀片基波电流,但又无法直接测量到;
、
、
是三相避雷器底部电流,可直接测量到,但受耦合电容影响;
、
、
是可直接测量,且只包含阀片基波电流,不受耦合电容电流的影响。
根据式(2),得到如图3所示的三相泄漏电流基波合成矢量图。定义其中
超前
的角度为α,
超前
的角度为β,
超前
的角度为γ。下面就分析一相MOA阻性基波电流变化导致α、β、γ的变化情况。
以上述典型MOA参数为例,泄漏电流基波有效值为0.4 mA,阻性电流基波与电压基波夹角为85˚。表3所示为各相阻性电流分别增加100%后,合成矢量角度变化量。

Table 2. Coupling capacitance of the total leakage current amplitude and phase angle of the rate of change
表2. 耦合电容对总泄漏电流幅值和相角的变化率

Table 3. The increase in resistive current leads to a table of composite vector angle changes
表3. 阻性电流增加导致合成矢量角度变化表
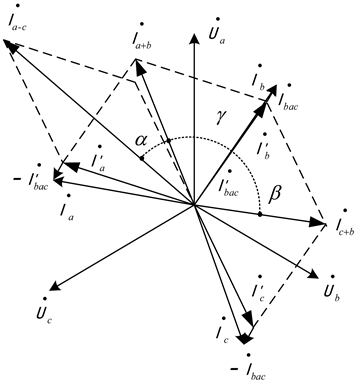
Figure 3. Three-phase leakage current fundamental synthesis vector illustration
图3. 三相泄漏电流基波合成矢量图
其中Δα、Δβ和Δγ分别为利用合成矢量定义的夹角变化量。
在实际应用当中,我们根据α、β和γ变化趋势来确定发生故障的避雷器,即当α、β和γ都变小时,A相避雷器发生故障,当α和γ变大,β变小时,B相避雷器发生故障,当α变小,β和γ变大时,C相避雷器发生故障。
6. 结论
本文采用矢量合成的方法去除了相间耦合电容对总泄漏电流的影响,并通过利用合成矢量定义的角度变化间接反映了阻性基波电流变化。在高压输电系统中,一般电压的幅值和相位变化很小,采用上述方法省去了电压信号的采集。该算法不仅简单,而且降低了硬件的绝对精度,易于结合嵌入式系统用于电力设备的在线监测,具有广阔的应用前景。