FRC对角斜筋小跨高比连梁多目标优化设计

Multi-Objective Optimization Design for FRC Diagonally Reinforced Coupling Beams with Small Span-to-Depth Ratio

摘要: 针对剪力墙结构中连梁工程造价及抗剪承载力问题，通过改变连梁基体材料及配筋方式，借鉴组合结构或构件多目标优化设计思路，对其进行优化设计，寻求更加经济可靠的设计方案。以FRC对角斜筋小跨高比连梁抗震性能试验研究为基础，将连梁的工程造价和抗剪承载力作为优化目标，引入加权系数构造评价函数，并借助复形法求最优解的思路，通过MATLAB编程实现非线性的多目标优化设计。结果表明，优化设计后，FRC对角斜筋小跨高比连梁的工程造价较传统设计连梁降低26%~42%；相应的抗剪承载力提高40%~60%。

Abstract: Aimed at the engineering cost and shear bearing capacity of coupling beam in shear wall structure, by changing the coupling material and reinforcement mode of the coupling beam, the mul-ti-objective optimization design idea of composite structure or component was adopted to optimize these coupling beams, so as to seek a more economical and reliable design plan. Taking the FRC diagonal reinforcement experimental study on seismic performance of short span coupling beams as the design foundation, the author chose beam engineering cost and shear bearing capacity as the optimization goals, introduced weighted coefficients to construct the evaluation function, and used the complex method for the optimal solutions of the multi-objective optimization design idea to realize the nonlinear multi-objective optimization design through MATLAB programming. The result showed that, compared with the conventional design, the engineering cost of the FRC diagonally reinforced coupling beams with small span-to-depth ratio reduced by 26%~42%, and the shear bearing capacity of them improved by 40%~60%.

1. 引言

小跨高比连梁属于反弯点在跨中的反对称弯曲深梁，剪弯比较大，难以避免在达到所需延性之前过早发生剪切破坏。为此，近年来各国学者主要通过以下几种方式来探究其受力性能，改善其抗剪承载力：1) 改变连梁主筋和箍筋配筋形式 [1] [2] [3] [4] ；2) 改善基体材料(混凝土)性能 [5] [6] ；3) 连梁中嵌入各类型钢 [7] [8] [9] ，Paulay [2] 通过研究对角斜筋配筋对连梁延性及耗能性能的影响发现，与普通配筋连梁相比，前者不仅有好的延性及耗能能力，而且施工方便，用钢量较小，但对于小跨高比试件，仍不能很好地满足抗震要求。而一些学者将改善混凝土材料和配筋形式两种方法相结合起来研究小跨高比连梁的抗剪性能。Canbolat等 [10] 提出将具有良好抗剪强度及耗能能力的纤维增强混凝土(FRC)应用于小跨高比连梁，并对4个不同配筋方式的FRC连梁进行试验研究。结果表明，用FRC替代普通混凝土作为连梁基体材料，可有效提高小跨高比连梁的承载力、延性和耗能能力。车佳玲 [11] 通过对4个不同跨高比，配箍率远小于规范要求的R/FRC连梁和1个普通混凝土材料对角斜筋小跨高比连梁试件进行拟静力试验，结果表明：具有明显应变硬化的FRC材料可有效提高小跨高比连梁的延性及耗能能力。梁兴文等 [12] [13] 通过对对角斜筋上设有拉结筋的小跨高比连梁进行拟静力试验研究，结果表明：跨高比不大于1.5的连梁，其破坏模式由原来的脆性剪切破坏转变为弯曲剪切的延性破坏，从而提高了小跨高比连梁的抗震性能。现有研究结果表明，两种方法相结合对于提高小跨高比连梁的抗剪切能力效果明显，为使FRC对角斜筋小跨高比连梁在一定的技术和物质条件下达到最佳的经济、性能要求，合理的优化设计至关重要。

本文借助复形法求最优解的思路 [14] ，将FRC对角斜筋小跨高比连梁的工程造价和抗剪承载力作为优化目标建立目标函数，通过调整加权系数，运用MATLAB程序实现优化过程，寻求各变量的最优组合，得到更加切合实际工程的FRC对角斜筋小跨高比连梁设计方案。

2. 优化设计

2.1. 设计变量

为实现最简优化设计，对FRC对角斜筋小跨高比连梁的相关参数作如下规定：1) 连梁净跨已知，通过调整连梁截面高度控制连梁跨高比；2) 混凝土、纵向钢筋、对角斜筋和箍筋的强度等级均根据我国《混凝土结构设计规范》 [15] 选取；3) 梁内箍筋间距最大值与箍筋直径最小值均满足《建筑抗震设计规范》 [16] 要求，不作为优化变量；4) 纵向受力钢筋和纵向构造筋均对称配置；5) FRC连梁保护层厚度按《高层建筑混凝土结构技术规程》 [17] 选取；6) FRC材料的抗压强度采用文献 [12] 中CB2-CB5的实测立方体抗压强度平均值。综合考虑变量灵敏度，设计变量可取为：X = [b, h, d_sd, n_sd, d_s, n_s, d_sb, n_sb, d_sv, s_sv]。其中：b、h为连梁截面的宽度和高度；d_sd，n_sd分别为对角斜筋的直径和数量；d_s，n_s分别为纵向受力钢筋的直径和数量；d_sb，n_sb分别为纵向构造钢筋的直径和数量；d_sv，s_sv分别为箍筋直径和间距。

2.2. 目标函数

同时将工程造价和抗剪承载力作为连梁优化设计目标，构造优化函数。通过单目标初始值消除量纲上的差异，为简化计算，同时引入加权系数和，采用线性加权法建立目标函数(抗剪承载力前加负号，即可求得目标函数最小值)，实现多目标优化向单目标优化转化 [18] [19] 。目标函数如下式(1)所示：

$\min F\left(X\right)=\alpha \frac{C\left(x\right)}{C_0}+\beta \left(-\frac{V\left(x\right)}{V_0}\right)$ (1)

式中： $\alpha$ 、 $\beta$ 均为加权系数，且 $\alpha >0,\beta >0$ ， $\alpha +\beta =1$ ； $C\left(x\right)$ 、 $V\left(x\right)$ 分别为连梁工程造价和抗剪承载力，表达式见公式(2)和公式(3)。 $C_0$ 、 $V_0$ 分别为连梁工程造价和抗剪承载力优化设计初始值。

连梁工程造价C(x)表达式如下：

$C\left(x\right)=C_1+C_2+C_3+C_4+C_5$ (2)

其中，

$C_1=C_f\left(bh-2A_s-2A_{sb}-2A_{sd}\right)$

$C_2=C_{\text{s}}\left(2A_{\text{s}}\right)$

$C_3=C_{\text{sb}}\left(2A_{\text{sb}}\right)$

$C_4=C_{\text{sd}}\left(2A_{\text{sd}}\right)$

$C_5=\frac{C_{sv}{A}_{sv}}{S_{sv}}$

式中： $C_1$ 、 $C_2$ 、 $C_3$ 、 $C_4$ 和 $C_5$ 分别为单位长度梁中的FRC混凝土、纵向受力筋、纵向构造筋、对角斜筋和箍筋的造价； $C_f$ 、 $C_s$ 、 $C_{sb}$ 、 $C_{sd}$ 和 $C_{sv}$ 分别是FRC混凝土、纵向受力筋、纵向构造筋、对角斜筋和箍筋的每平方米单价； $A_s$ 为单侧纵向受力筋的截面面积； $A_{sb}$ 为单侧纵向构造筋的截面面积； $A_{sd}$ 为单向对角斜筋的截面面积； $A_{sv}$ 为连梁截面内箍筋面积总和； $S_{sv}$ 为连梁中箍筋间距。抗剪承载力V(x)表达式如下 [11] ：

$V\left(x\right)=1.2a_{s}b{f^{\prime }}_c\sin \alpha +2A_{sd}{f}_{sd}\sin \alpha$ (3)

式中：a_s为FRC斜压杆截面高度；α为对角斜筋与水平方向的夹角；A_sd和f_sd分别为单侧对角斜筋面积和屈服强度； ${f^{\prime }}_c$ 为FRC轴心抗压强度。

2.3. 约束条件

2.3.1. 正截面抗弯承载力要求

根据《混凝土结构设计规范》(GB 50010-2010) [15] ，连梁正截面抗弯承载力验算，应满足下式规定：

${\gamma }_{0}M\le M_u$ (4)

式中： ${\gamma }_0$ 为结构重要性系数；弯矩M(连梁正截面的弯距设计值)已给出， $M_u$ 为考虑地震作用组合的连梁正截面受弯承载力设计值。

2.3.2. 受剪截面限制条件

根据我国现行《混凝土结构设计规范》(GB 50010-2010) [15] ，跨高比不大于2.5，配置普通箍筋的筒体及剪力墙洞口连梁，其截面应满足下列约束条件：

1) 受剪截面承载力V_wb应符合：

$V_{\text{wb}}\le \frac{1}{{\gamma }_{RE}}\left(0.15{\beta }_c{f}_{c}b{h}_0\right)$ (5)

2) 斜截面受剪承载力应满足以下规定：

$V_{\text{wb}}\le \frac{1}{{\gamma }_{RE}}\left[0.38f_t{b}_{\text{b}}{h}_{b0}+0.9f_{y\text{v}}\frac{A_{sv}}{s}{h}_{b0}\right]$ (6)

2.3.3. 构造约束

1) 连梁截面尺寸

根据我国现行《混凝土结构设计规范》(GB 50010-2010)规定 [15] ，对一级、二级抗震等级下，跨高比不大于2.5且连梁截面宽度不小于250 mm时，梁内可配置交叉斜筋；

2) 纵向受力钢筋

根据《高层建筑混凝土结构技术规程》(JGJ 3-2010) [17] 规定：跨高比(l_n/h)不超过1.5的连梁，采用非抗震设计时，其纵向钢筋的最小配筋率 ${\rho }_{s\min }$ 取0.2%；抗震设计时，宜满足表1要求。此外，剪力墙结构中的非抗震设计连梁，其顶面及底面单侧纵向钢筋最大配筋率 ${\rho }_{s\max }$ ≤ 2.5%；若采用抗震设计，其顶面及底面单侧纵向钢筋的最大配筋率宜符合表2要求。

3) 纵向构造钢筋

根据《高层建筑混凝土结构技术规程》(JGJ 3-2010) [17] 规定：截面高度大于700mm的连梁在进行纵向构造钢筋配置时需满足下列要求： $d_{sb}\ge 10\text{mm}$ ， $n_{sb}\ge 2$ ， $s_{sb}\le 200\text{mm}$ ， ${\rho }_{Asb}\ge 0.3\%$ 。

4) 箍筋

《高层建筑混凝土结构技术规程》(JGJ 3-2010) [17] 规定：抗震设计时，梁内箍筋最大间距及最小直径要求如表3所示。若梁端纵向钢筋配筋率大于2%时，则相应的箍筋最小直径增加2 mm。

5) 对角斜筋

若同一方向的对角斜筋根数n_sd > 1时，应对其设置拉结筋，其间距采用梁宽和300 mm中的较小值，且直径不应小于6 mm。

6) 连梁试件保护层厚度按照《高层建筑混凝土结构技术规程》(GB 50010-2010)选取。

考虑到优化设计后连梁尺寸及配筋需满足规范最低标准，所以，通过Matlab将上述所有约束条件编写为主程序中的调用函数，检验设计变量是否满足规范要求。约束条件的严格程度将影响优化结果的优劣性。

Table 1. Minimum reinforcement ratio (%) for longitudinal reinforced bars with span -height ratio not greater than 1.5

表1. 跨高比l_n/h不大于1.5的连梁纵向钢筋的最小配筋率(%)

Table 2. Maximum reinforcement ratio (%) for longitudinal reinforcement of coupling beams

表2. 连梁纵向钢筋的最大配筋率(%)

Table 3. Maximum spacing and minimum diameter of stirrups (mm)

表3. 箍筋最大间距及最小直径(mm)

3. 求解手段及步骤

利用复形法求最优解 [18] 已经成为非线性优化设计的一种通用手段。复形法即在n维受非线性约束的可行空间内，由K > (n + 1)个顶点构成多面体。其迭代过程是对复形各顶点的函数值逐一进行比较，不断舍去函数值最劣的顶点，逐步逼近，直到目标函数收敛得到最优点。复形法的思想源自单纯形法，但较单纯形法更为灵活可变。复形法的迭代步骤大致如下：1) 根据经验值构成初始复形；2) 寻求映象点；3) 计算映象点函数值并与最劣点进行比较；4) 收敛判断得出最优解。综上所述，复形法在求解最优解的过程中，检验了整个设计区域，较目标函数及约束函数求导等方法所求结果更可靠。本文利用复形法的优化思想，通过MATLAB编程，迭代计算FRC小跨高比连梁在上述设计变量下的最优解。优化流程框图如图1所示。首先编写主程序，输入目标函数，并将设计变量对应的约束条件作为调用函数，然后为设计变量依次赋初值，最后运行主函数，求出目标函数最小值及其对应的设计参数值。若变量不满足约束条件，则重新赋值，重新计算。

Figure 1. Optimization design flow chart

图1. 优化设计流程图

4. 算例分析

基于上述优化设计方案，设计2个净跨分别为900 mm和1200 mm的纤维增强混凝土连梁试件，编号为L₁、L_2。为了对比分析，同时设计了1个与L₁仅基体材料抗压强度不同的连梁试件，编号为L₃。优化前连梁基体采用强度等级为C40的普通混凝土；优化设计时采用纤维增强混凝土(FRC)，且抗压强度以文献 [11] 中尺寸为100 × 100 × 100 mm的立方体试块实测值为标准。纵向钢筋和对角斜筋均采用HRB400，箍筋采用HRB335，其力学性能指标均按现行规范选取。材料单价取值：FRC混凝土为300元/m³；纵向钢筋为3200元/t；箍筋为3000元/t。

4.1. 优化前后连梁尺寸及配筋对比

由PKPM完成常规设计。为了消除量纲上的差异，同时加快程序收敛，引入优化前常规设计得到的工程造价和抗剪承载力值作为优化初始值。优化前、后连梁尺寸及配筋图分别如图2(a)、图2(b)所示。将试件L₁优化前和优化后的各设计参数列于表4，分别取α = 0.4，β = 0.6和α = 0.6，β = 0.4两种加权系数对L₁进行优化。从表4中可看到，当α = 0.4，β = 0.6时，工程造价与优化前相当，但连梁斜截面承载力比优化前提高69%；当α = 0.6、β = 0.4时，抗剪承载力略高于优化前，而工程造价较优化前降低26%。

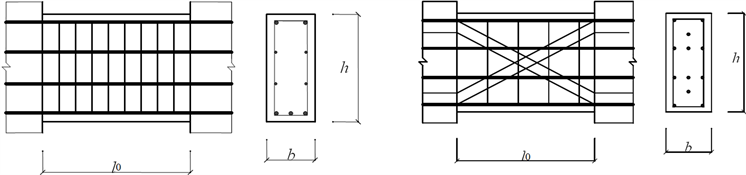(a) 优化前连梁尺寸及配筋 (b) 优化后连梁尺寸及配筋

Figure 2. Optimization of the size and reinforcement diagram of the coupling beam before and after

图2. 优化前后连梁尺寸及配筋图

Table 4. Comparison of optimization design parameters before and after of L1

表4. 试件L₁优化前后设计参数对比

4.2. 优化结果分析

将L_1、L_2、L₃三个试件在不同加权系数下对应的优化结果列于下表5、表6和表7所示。

Table 5. Optimization results of specimen L1 under different weighting coefficients

表5. 试件L₁在不同加权系数下的优化结果

Table 6. Optimization results of specimen L2 under different weighting coefficients

表6. 试件L₂在不同加权系数下的优化结果

注：梁L₂优化前的工程造价(C₀)和抗剪承载力(V₀)分别为819.15元∙m⁻¹和834.22 kN。

Table 7. Optimization results of specimen L3 under different weighting coefficients

表7. 试件L₃在不同加权系数下的优化结果

注：梁L₃优化前的工程造价(C₀)和抗剪承载力(V₀)分别为836.20元∙m⁻¹和613.68 kN。

为了能直观地说明加权系数与两个优化目标之间的关系，将上述3个表格中优化所得数据绘制如图3(a)、图3(b)所示。

对图3作如下分析说明：

1) 优化结果表明，连梁工程造价和斜截面抗剪承载力均随着加权系数α的增加而呈下降趋势，与连梁跨高比和基体材料抗压强度无关。

2) 3个试件的优化结果均表明：当α = 0、β = 1.0时，只考虑了构件抗剪承载力，工程造价最高；当α = 1.0、β = 0时，抗剪承载力相应的约束失效，工程造价达到最小值。此时，多目标优化转化为单目标优化。

3) 当α较小时(0 < α < 0.4)，仅斜截面抗剪承载力得到了优化；当α较大时(0.60 < α < 1.00)，仅造价得到了优化；而3个试件的优化结果均表明，当0.4 ≤ α ≤ 0.6，且工程造价与优化前相当时，连梁斜截面

(a) 加权系数α与工程造价的关系 (b) 加权系数α与抗剪承载力的关系

Figure 3. The relationship between weighted coefficient α and optimal objectives

图3. 加权系数α与优化目标之间的关系

承载力比优化前提高40%~60%；反过来，当抗剪承载力值与优化前相差不多时，工程造价较优化前降低了26%~42%。此时，连梁抗剪性能和工程造价都得到了一定程度的优化。

4) 从表5和表6中的优化数据可知，跨高比较大的连梁，其抗剪承载力略低。

5. 结论

采用组合结构构件的多目标设计方法，将成熟的单目标优化理念应用于多目标优化设计，将复形法求解最优值的理念与计算机程序相结合，求得了FRC对角斜筋小跨高比连梁的多目标优化设计。并得到以下结论：

1) 由三个不同跨高比的连梁试件的优化结果表明，当0.4 ≤ α ≤ 0.6时，连梁抗剪性能和工程造价都得到了一定程度的优化：若工程造价与优化前相当，则连梁斜截面承载力比优化前提高40%~60%；反过来，当抗剪承载力值与优化前相差不多时，工程造价较优化前降低了26%~42%。总之，经优化设计后，不仅连梁抗剪承载力明显提高，同时降低了工程造价，节省工程成本。

2) 通过同时改变连梁基体材料及配筋方式，综合考虑两个优化目标，运用本文提出的优化方法对其进行优化设计，结果表明，此方法合理可行。

致谢

值此论文完成之际，感谢国家自然科学基金项目“R/ECC联肢剪力墙结构基于最优屈服机制的抗震性能设计理论与方法”，感谢宁夏青年科技人才托举工程，感谢宁夏大学研究生创新项目“基于目标侧移和耦联率的R/FRC联肢墙抗震性能设计”提供的基金资助。

基金项目

国家自然科学青年基金项目(51408328)；宁夏青年科技人才托举工程；宁夏大学研究生创新项目(GIP2018056)。