(2 + 1)维色散的长波方程的新精确解
New Exact Solutions for (2 + 1)-Dimensional Dispersive Long Wave Equation
摘要: 利用一种基于符号计算的代数方法，结合Maple环境中的Epsilon软件包，求解(2 + 1)维色散的长波方程，获得了若干其它方法不曾给出的形式更为丰富的新的显式行波解，其中包括孤波解、三角函数解、双曲函数解。
Abstract: The algebraic method, based on the symbolic computation, has been applied to study new traveling wave solutions for (2 + 1)-dimensional dispersive long wave equations by means of Epsilon package in Maple. More new explicit travelling wave solutions are obtained, which contain solitons, hyperbola function solutions and triangular periodic solutions.
文章引用：傅海明. (2 + 1)维色散的长波方程的新精确解[J]. 理论数学, 2018, 8(6): 589-595. https://doi.org/10.12677/PM.2018.86079

1. 引言

孤立子的研究工作在全世界范围掀起了一股热潮，不仅仅在流体物理，固体物理，基本粒子物理和量子物理等领域中，在凝聚太物理，超导物理等领域中都开展了孤立子的研究。近年来，学者们发现了求解非线性偏微分方程的大量方法，这些方法主要有Banach不动点理论、逆散射法 [1] 、算子半群理论、Backlund法 [2] 、调和分析法、Darboux变换法 [3] 、Galerkin方法、Hirota双线性法 [4] [5] [6] 和Painlevé展开法 [7] 等。结合计算机数学软件(如MATLAB等)，又发展了许多新的求解非线性偏微分波方程的方法，例如双曲函数法 [8] 、代数几何法、齐次平衡法 [9] 、特殊包络变换法 [10] [11] 、双指数函数法 [12] 和F-展开法 [13] [14] [15] 等。

2. (2 + 1)维色散的长波方程的新精确解

为了求得(2 + 1)维色散的长波方程

{ u y t + v x x + 1 2 ( u 2 ) x y = 0 v t + ( u v + u + u x y ) x = 0 , (1)

的行波解，我们先设该方程的有如下形式的行波变换：

u ( x , y , t ) = u ( ξ ) , v ( x , y , t ) = v ( ξ )   ( ξ = k x + h y + w t + ξ 0 ) , (2)

其中 k , h , w 为代定实常数， ξ 0 为任意实常数。把式(2)代入(2 + 1)维色散的长波方程，并且积分两次，积分常数设为零，可得

{ h w u + k 2 v + 1 2 k h u 2 = 0 w v + k u v + k u + k 2 h u ξ ξ = 0 . (3)

设上面方程中的 u ( ξ ) 和 v ( ξ ) 为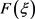的有限项级数形式，如下：

u ( ξ ) = ∑ i = 1 n a i F i ( ξ ) + a 0 , v ( ξ ) = ∑ i = 1 m b i F i ( ξ ) + b 0 , (4)

而 F ( ξ ) 满足一阶非线性常微分方程：

( F ′ ) 2 = h 6 F 6 + h 4 F 4 + h 2 F 2 + h 0 . (5)

平衡非线性常微分方程(3)中的 u ( ξ ) 和最高阶导数项与最高次非线性项，得 m = 2 , n = 4 ，即

(6)

把式(6)代入非线性常微分方程(3)，并利用常微分方程(5)可以得到关于 F i ( ξ ) , ( i = 0 , 1 , 2 , ⋯ , 6 ) 的方程，设其各次方的系数为零，得到如下超越代数方程组：

k h a 2 2 + 2 k 2 b 4 = 0 , (7)

k h a 1 a 2 + k 2 b 3 = 0 , (8)

k h ( a 1 2 + 2 a 0 a 2 ) + 2 k 2 b 2 + 2 h w a 2 = 0 , (9)

k h a 0 a 1 + k 2 b 1 + h w a 1 = 0 , (10)

k h a 0 2 + 2 k 2 b 0 + 2 h w a 0 = 0 , (11)

8 k 2 h a 2 h 6 + k a 2 b 4 = 0 , (12)

3 k 2 h a 1 h 6 + k ( a 1 b 4 + a 2 b 3 ) = 0 , (13)

6 k 2 h a 2 h 4 + k ( a 0 b 4 + a 1 b 3 + a 2 b 2 ) + w b 4 = 0 , (14)

2 k 2 h a 1 h 4 + k ( a 0 b 3 + a 1 b 2 + a 2 b 1 ) + w b 3 = 0 , (15)

4 k 2 h a 2 h 2 + k ( a 0 b 2 + a 1 b 1 + a 2 b 0 ) + w b 2 + k a 2 = 0 , (16)

k 2 h a 1 h 2 + k ( a 0 b 1 + a 1 b 0 ) + w b 1 + k a 1 = 0 , (17)

2 k 2 h a 2 h 0 + k a 0 b 0 + w b 0 + k a 0 = 0 , (18)

利用Maple求解以上超越代数方程组，得到下面这组解：

a 1 = 0 , b 1 = 0 , b 3 = 0 , a 2 = 4 k h 6 , a 0 = k B , b 4 = 8 ( b 0 + 1 ) h 6 2 4 h 2 h 6 − h 4 2 , b 2 = 4 ( b 0 + 1 ) h 4 h 6 4 h 2 h 6 − h 4 2 ,

h = ( b 0 + 1 ) h 6 k ( h 4 2 − 4 h 2 h 6 ) , w = k 2 h 6 ( h 4 h 6 − B ) , k为任意常数, (19)

而 b 0 由下式给出：

8 ( b 0 + 1 ) h 0 h 6 2 h 6 = ( 4 h 2 h 6 − h 4 2 ) ( B + b 0 h 4 h 6 ) , (20)

其中， B = h 4 h 6 ± h 4 2 h 6 ( 3 b 0 + 1 ) − 8 b 0 h 2 h 6 2 b 0 + 1 。

情形1：当 h 2 > 0 时，非线性常微分方程(5)有如下双曲函数解： F 1 = ( − h 2 h 4 s e c h 2 ( h 2 ξ ) h 4 2 − h 2 h 6 ( 1 ± tanh ( h 2 ξ ) ) 2 ) 1 2 ， F 2 = ( h 2 h 4 c s c h 2 ( h 2 ξ ) h 4 2 − h 2 h 6 ( 1 ± coth ( h 2 ξ ) ) 2 ) 1 2 ， F 3 = 4 ( h 2 exp ( ± 2 h 2 ξ ) ( exp ( ± 2 h 2 ξ ) − 4 h 4 ) 2 − 64 h 2 h 6 ) 1 2 。将这些解代入式(6)，得到(2 + 1)维色散的长波方程的行波解为：

{ u 1 = k B + 4 k h 6 − h 2 h 4 s e c h 2 ( h 2 ξ ) h 4 2 − h 2 h 6 ( 1 ± tanh ( h 2 ξ ) ) 2 v 1 = b 0 − 4 ( b 0 + 1 ) 4 h 2 h 6 − h 4 2 { h 2 h 4 2 h 6 s e c h 2 ( h 2 ξ ) h 4 2 − h 2 h 6 ( 1 ± tanh ( h 2 ξ ) ) 2 − 2 ( h 2 h 4 h 6 s e c h 2 ( h 2 ξ ) h 4 2 − h 2 h 6 ( 1 ± tanh ( h 2 ξ ) ) 2 ) 2 } ,

{ u 2 = k B + 4 k h 6 h 2 h 4 c s c h 2 ( h 2 ξ ) h 4 2 − h 2 h 6 ( 1 ± coth ( h 2 ξ ) ) 2 v 2 = b 0 + 4 ( b 0 + 1 ) 4 h 2 h 6 − h 4 2 { h 2 h 4 2 h 6 c s c h 2 ( h 2 ξ ) h 4 2 − h 2 h 6 ( 1 ± coth ( h 2 ξ ) ) 2 + 2 ( h 2 h 4 h 6 c s c h 2 ( h 2 ξ ) h 4 2 − h 2 h 6 ( 1 ± coth ( h 2 ξ ) ) 2 ) 2 } ,

{ u 3 = k B + 64 k h 6 h 2 exp ( ± 2 h 2 ξ ) ( exp ( ± 2 h 2 ξ ) − 4 h 4 ) 2 − 64 h 2 h 6 v 3 = b 0 + 64 ( b 0 + 1 ) 4 h 2 h 6 − h 4 2 { h 2 h 4 h 6 exp ( ± 2 h 2 ξ ) ( exp ( ± 2 h 2 ξ ) − 4 h 4 ) 2 − 64 h 2 h 6 + ( 4 2 h 2 h 6 exp ( ± 2 h 2 ξ ) ( exp ( ± 2 h 2 ξ ) − 4 h 4 ) 2 − 64 h 2 h 6 ) 2 } ,

其中， ξ = k x + ( b 0 + 1 ) h 6 k ( h 4 2 − 4 h 2 h 6 ) y + k 2 h 6 ( h 4 h 6 − B ) t + ξ 0 ， k , ξ 0 为任意常数。

情形2：当 h 2 > 0 , h 4 2 − 4 h 2 h 6 > 0 时，非线性常微分方程(5)有如下双曲函数解：

F 4 = ( 2 h 2 ± h 4 2 − 4 h 2 h 6 cosh ( 2 h 2 ξ ) − h 4 ) 1 2 ，把 F 4 代入式(6)，得到(2 + 1)维色散的长波方程的行波解为：

{ u 4 = k B + 4 k h 6 2 h 2 ± h 4 2 − 4 h 2 h 6 cosh ( 2 h 2 ξ ) − h 4 v 4 = b 0 + 8 ( b 0 + 1 ) 4 h 2 h 6 − h 4 2 { h 2 h 4 h 6 ± h 4 2 − 4 h 2 h 6 cosh ( 2 h 2 ξ ) − h 4 + ( 2 h 2 h 6 h 4 2 − 4 h 2 h 6 cosh ( 2 h 2 ξ ) ∓ h 4 ) 2 } ,

其中， ξ = k x + ( b 0 + 1 ) h 6 k ( h 4 2 − 4 h 2 h 6 ) y + k 2 h 6 ( h 4 h 6 − B ) t + ξ 0 ， k , ξ 0 为任意常数。

情形3：当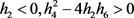时，非线性常微分方程(5)有如下三角函数解：

，把 F 5 代入式(6)，得到(2 + 1)维色散的长波方程的周期行波解为：

{ u 5 = k B + 4 k h 6 2 h 2 ± h 4 2 − 4 h 2 h 6 cos ( 2 − h 2 ξ ) − h 4 v 5 = b 0 + 8 ( b 0 + 1 ) 4 h 2 h 6 − h 4 2 { h 2 h 4 h 6 ± h 4 2 − 4 h 2 h 6 cos ( 2 − h 2 ξ ) − h 4 + ( 2 h 2 h 6 h 4 2 − 4 h 2 h 6 cos ( 2 − h 2 ξ ) ∓ h 4 ) 2 }

其中， ξ = k x + ( b 0 + 1 ) h 6 k ( h 4 2 − 4 h 2 h 6 ) y + k 2 h 6 ( h 4 h 6 − B ) t + ξ 0 ， k , ξ 0 为任意常数。

情形4：当 h 2 > 0 , h 4 2 − 4 h 2 h 6 < 0 时，非线性常微分方程(5)有如下双曲函数解：

F 6 = ( 2 h 2 ± − h 4 2 + 4 h 2 h 6 sinh ( 2 h 2 ξ ) − h 4 ) 1 2 ，把 F 6 代入式(6)，得到(2 + 1)维色散的长波方程的行波解为：

{ u 6 = k B + 4 k h 6 2 h 2 ± − h 4 2 + 4 h 2 h 6 sinh ( 2 h 2 ξ ) − h 4 v 6 = b 0 + 8 ( b 0 + 1 ) 4 h 2 h 6 − h 4 2 { h 2 h 4 h 6 ± − h 4 2 + 4 h 2 h 6 sinh ( 2 h 2 ξ ) − h 4 + ( 2 h 2 h 6 − h 4 2 + 4 h 2 h 6 sinh ( 2 h 2 ξ ) ∓ h 4 ) 2 }

其中， ξ = k x + ( b 0 + 1 ) h 6 k ( h 4 2 − 4 h 2 h 6 ) y + k 2 h 6 ( h 4 h 6 − B ) t + ξ 0 ， k , ξ 0 为任意常数。

情形5：当 h 2 < 0 , h 4 2 − 4 h 2 h 6 < 0 时，非线性常微分方程(5)有如下三角函数解：

F 7 = ( 2 h 2 ± − h 4 2 + 4 h 2 h 6 sin ( 2 − h 2 ξ ) − h 4 ) 1 2 ，把 F 7 代入式(6)，得到(2 + 1)维色散的长波方程的周期行波解为：

{ u 7 = k B + 4 k h 6 2 h 2 ± − h 4 2 + 4 h 2 h 6 sin ( 2 − h 2 ξ ) − h 4 v 7 = b 0 + 8 ( b 0 + 1 ) 4 h 2 h 6 − h 4 2 { h 2 h 4 h 6 ± − h 4 2 + 4 h 2 h 6 sin ( 2 − h 2 ξ ) − h 4 + ( 2 h 2 h 6 − h 4 2 + 4 h 2 h 6 sin ( 2 − h 2 ξ ) ∓ h 4 ) 2 }

其中， ξ = k x + ( b 0 + 1 ) h 6 k ( h 4 2 − 4 h 2 h 6 ) y + k 2 h 6 ( h 4 h 6 − B ) t + ξ 0 ， k , ξ 0 为任意常数。

情形6：当 h 2 > 0 , h 6 > 0 时，非线性常微分方程(5)有如下双曲函数解： F 8 = ( − h 2 s e c h 2 ( h 2 ξ ) h 4 ± 2 h 2 h 6 tanh ( h 2 ξ ) ) 1 2 ，把 F 8 代入式(6)，得到(2 + 1)维色散的长波方程的行波解为：

{ u 8 = k B + 4 k h 6 − h 2 s e c h 2 ( h 2 ξ ) h 4 ± 2 h 2 h 6 tanh ( h 2 ξ ) v 8 = b 0 + 4 ( b 0 + 1 ) h 4 h 6 4 h 2 h 6 − h 4 2 − h 2 s e c h 2 ( h 2 ξ ) h 4 ± 2 h 2 h 6 tanh ( h 2 ξ ) + 8 ( b 0 + 1 ) h 6 2 4 h 2 h 6 − h 4 2 ( − h 2 s e c h 2 ( h 2 ξ ) h 4 ± 2 h 2 h 6 tanh ( h 2 ξ ) ) 2 ,

其中， ξ = k x + ( b 0 + 1 ) h 6 k ( h 4 2 − 4 h 2 h 6 ) y + k 2 h 6 ( h 4 h 6 − B ) t + ξ 0 ， k , ξ 0 为任意常数。

情形7：当 h 2 < 0 , h 6 > 0 时，非线性常微分方程(5)有如下三角函数解： F 9 = ( − h 2 sec 2 ( − h 2 ξ ) h 4 ± 2 − h 2 h 6 tan ( − h 2 ξ ) ) 1 2 ，把 F 9 代入式(6)，得到(2 + 1)维色散的长波方程的周期行波解为：

{ u 9 = k B + 4 k h 6 − h 2 sec 2 ( − h 2 ξ ) h 4 ± 2 − h 2 h 6 tan ( − h 2 ξ ) v 9 = b 0 + 4 ( b 0 + 1 ) h 4 h 6 4 h 2 h 6 − h 4 2 − h 2 sec 2 ( − h 2 ξ ) h 4 ± 2 − h 2 h 6 tan ( − h 2 ξ ) + 8 ( b 0 + 1 ) h 6 2 4 h 2 h 6 − h 4 2 ( − h 2 sec 2 ( − h 2 ξ ) h 4 ± 2 − h 2 h 6 tan ( − h 2 ξ ) ) 2

其中， ξ = k x + ( b 0 + 1 ) h 6 k ( h 4 2 − 4 h 2 h 6 ) y + k 2 h 6 ( h 4 h 6 − B ) t + ξ 0 ， k , ξ 0 为任意常数。

情形8：当 h 2 > 0 , h 4 < 0 , h 0 = 8 h 2 2 27 h 4 , h 6 = h 4 2 4 h 2 时，非线性常微分方程(5)有如下三角函数解：

F 10 = ( 8 h 2 tan 2 ( ± h 2 / 3 ξ ) 3 h 4 ( 3 − tan 2 ( ± h 2 / 3 ξ ) ) ) 1 2 ， ，将这些三角函数解代入式(6)，得到(2 + 1)维色散的长波方程的周期行波解为：

{ u 10 = k B + 4 k h 6 8 h 2 tan 2 ( ± h 2 / 3 ξ ) 3 h 4 ( 3 − tan 2 ( ± h 2 / 3 ξ ) ) v 10 = b 0 + 4 ( b 0 + 1 ) h 4 h 6 4 h 2 h 6 − h 4 2 8 h 2 tan 2 ( ± h 2 / 3 ξ ) 3 h 4 ( 3 − tan 2 ( ± h 2 / 3 ξ ) ) + 8 ( b 0 + 1 ) h 6 2 4 h 2 h 6 − h 4 2 ( 8 h 2 tan 2 ( ± h 2 / 3 ξ ) 3 h 4 ( 3 − tan 2 ( ± h 2 / 3 ξ ) ) ) 2 ,

{ u 11 = k B + 4 k h 6 8 h 2 cot 2 ( ± h 2 / 3 ξ ) 3 h 4 ( 3 − cot 2 ( ± h 2 / 3 ξ ) ) v 11 = b 0 + 4 ( b 0 + 1 ) h 4 h 6 4 h 2 h 6 − h 4 2 8 h 2 cot 2 ( ± h 2 / 3 ξ ) 3 h 4 ( 3 − cot 2 ( ± h 2 / 3 ξ ) ) + 8 ( b 0 + 1 ) h 6 2 4 h 2 h 6 − h 4 2 ( 8 h 2 cot 2 ( ± h 2 / 3 ξ ) 3 h 4 ( 3 − cot 2 ( ± h 2 / 3 ξ ) ) ) 2 ,

其中， ξ = k x + ( b 0 + 1 ) h 6 k ( h 4 2 − 4 h 2 h 6 ) y + k 2 h 6 ( h 4 h 6 − B ) t + ξ 0 ，为任意常数。

3. 结论

本文利用行波变换法得到(2 + 1)维色散的长波方程的若干新的显式行波解，其中包括非周期孤立波解和周期孤立波解，这些行波解还包括爆破波解、周期爆破波解等。同时，容易看出该方法还是很高效的，可以运用于求解其它非线性波方程，同样能得到非常丰富的行波解。

基金项目

广东省教育厅特色创新类项目(2017GKTSCX111)。

参考文献

[1] Ablowitz, M.J. and Clarkson, P.A. (1991) Soliton, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge, 123-136.
https://doi.org/10.1017/CBO9780511623998
[2] 谷超豪. 孤立子理论及其应用[M]. 杭州: 浙江科技出版社, 1990: 86-98.
[3] Matveev, V.B. and Salle, M.A. (1991) Daroux Transformations and Solitons. Springer, Berlin, 326-387.
https://doi.org/10.1007/978-3-662-00922-2
[4] 傅海明, 戴正德. (3 + 1)维K-P方程的周期孤波解[J]. 山西大学学报(自然科学版), 2010, 33(1): 4-7.
[5] 傅海明, 戴正德. Jimbo-Miwa方程的周期孤波解[J]. 河南科技大学学报(自然科学版), 2009, 30(3): 92-95.
[6] 傅海明, 戴正德. (3 + 1)维孤子方程的周期孤波解[J]. 东北师范大学学报(自然科学版), 2011, 47(2): 32-34, 42.
[7] 楼森岳. 推广的Painlevé展开及KdV方程的非标准截断解[J]. 物理学报, 1998, 47(12): 1739-1745.
[8] 李志斌, 张善卿. 非线性波方程准确孤立波解的符号计算[J]. 数学物理学报, 1997, 17(1): 81-89.
[9] Wang, M.L., Zhou, Y.B. and Li, Z.B. (1996) Application of Homogeneous Balance Method to Exact Solutions of Nonlinear Equations in Mathematical Physics. Physics Letters A, 213, 67-75.
https://doi.org/10.1016/0375-9601(96)00283-6
[10] Fu, H.-M. and Dai, Z.D. (2010) Exact Chirped Solitary-Wave Solutions for Ginzburg-Landau Equation. Communications in Nonlinear Science and Numerical Simulations, 15, 1462-1465.
https://doi.org/10.1016/j.cnsns.2009.06.006
[11] 傅海明, 戴正德. (2+1)维破裂孤子方程的周期孤立波解[J]. 江苏师范大学学报: 自然科学版, 2018, 36(1): 40-42.
[12] Fu, H.-M. and Dai, Z.-D. (2009) Double Exp-Function Method and Application. In-ternational Journal of Nonlinear Science and Numerical Simulation, 10, 927-933.
https://doi.org/10.1515/IJNSNS.2009.10.7.927
[13] 傅海明, 戴正德. 耦合Klein-Gordon-Schrodinger方程的新精确解[J]. 西北师范大学学报(自然科学版), 2009, 45(6): 32-34, 42.
[14] 傅海明, 戴正德. (2 + 1)维Nizhnik-Novikov-Veselov方程组的新精确解[J]. 山东师范大学学报(自然科学版), 2009, 24(3): 6-8.
[15] 傅海明, 戴正德. 新辅助函数法及(2 + 1)维Burgers方程的精确解[J]. 江苏师范大学学报(自然科学版), 2015, 33(4): 25-29.

为你推荐