1. 引言
波浪破碎是波浪传播到近岸区域后,受到地形的限制而产生的变形、折射、绕射、反射等作用后产生的剧烈形态变化。波浪破碎对海岸带、沿海城市、交通枢纽、国防建设等一系列的基础设施造成了威胁,对沿岸人民的生活有较大的影响,所以对于近岸地区波浪传播与破碎运动的研究十分之重要 [1] 。
根据破碎后的形态,波浪破碎可分为崩破波、卷破波、激破波三种类型 [2] 。三种类型中,激破波的破碎形式最复杂,其现象为:在波峰前沿根部开始出现破碎现象,随后波峰前沿部分呈非常杂乱的破碎状态,并沿斜坡上爬。波峰前沿的杂乱部分,由于水质点存在极大的不规则特性,则成为了数值模拟的大难题。河海大学诸裕良 [3] 利用波浪水槽实验研究了复合坡度下的破碎变化形态,虽然地形符合激破波的条件,但实验过程中却没有观测到明显的激破现象。郄禄文 [4] [5] 则用SPH方法模拟了三种破碎形式下的速度变化和波峰压力,但对激破波的形态并未作特别的关注。天津大学赵京津 [6] 做了激破波的相关水槽实验,并用光滑粒子方法模拟了波浪的爬坡过程,但未针对激破波的现象做细致的研究。
由于在波浪破碎的过程中,波浪的自由表面发生扭曲,随后大量的水质点发生分离,整个运动过程中自由表面的形态产生了较大的变化。如用常规网格来计算,处理难度较大。面对形态复杂的激破波,SPH方法是一种比较实用的数值方法。由于流体的自由表面在粒子形态下被离散化,流体模拟技术能逼真地模拟各种复杂流体现象,能直观地呈现各种自由表面的复杂变形 [7] 。目前,在波浪破碎的数值模拟中,SPH已大量得到应用 [8] [9] [10] 。
本文利用SPH方法对激破波展开研究,首先将通过试验结果来验证SPH方法的准确性,随后将对激破波展开细致的研究,结合数值模拟图形来分析激破波波前散碎波浪的特性。由于波浪形态用光滑的离散粒子来表示,得到的结果具备很好的直观性。对激破波发生波浪破碎的时间和位置,本文将做重点的关注。
2. 激破波形式及发生条件
2.1. 激破波简介
激破波是破碎形态中形态变化比较剧烈一种破碎现象。在波浪的运动推进的过程中,在近岸的斜坡上发生破碎时,首先前沿面会首先变得陡立,然后卷曲拱形。但是,当坡度比较陡的时候,波浪无法形成卷曲形态进行翻卷,而是会转化成大量的散碎的水花向前运动。此时,波峰前后逐渐变的非常不对称,波浪的形态已经基本消失。
而激破波此时所表现出的现象为波峰前沿根部开始出现破碎现象,随后波峰前沿部分呈非常杂乱的破碎状态,并沿斜坡上爬。但是,由于波浪前端的形态已经转化为杂乱的水质点,这些水质点无法形成状态规则的自由表面。等到水质点重新落回水面以后,形成流动状态比较复杂的一股水流。整个激破波的变化形态如图1所示,波峰前存在着从陡立形态到激破形态的几个阶段。

Figure 1. The variation of the shape of surging breaking wave
图1. 激破波形态变化
从发生波浪破碎位置,到岸边的一段区域,称为破碎带。在破碎带中,水的深度从破碎点到岸边逐渐减小,波浪将一直延续破碎状态。水体的湍流和涡度非常强,是波浪能大量的消耗,且水质点的运动形态非线性较强,波形,能量消耗,湍流和漩涡的剧烈变化非常强烈。
2.2. 激破波发生条件
根据Galvin的实验 [2] ,波浪破碎形态可根据破波相似参数来进行区分,这里定义深水处的相似参数为
,破碎处的相似参数为
。它们的计算方式为:
(1)
这里,H0和Hb分别为深水处和破碎处的波高,L0为深水处波长,b为坡度的倾斜角。波浪破碎后的类型,区分依据如表1:

Table 1. The types of breaking form
表1. 破碎形态分类
从表1中可以看出,波浪类型与坡面的斜度关系较为密切。当坡度较为缓和时,波浪能维持正常形态。随着水底的坡度逐渐倾斜,水深不断变浅,此时波长逐渐缩短,波高逐渐增大。当波高波长比增大到一定程度时,波浪维持正常形态的难度会变大。若坡度较缓和,则波峰顶部开始出现白色浪花,此时表现为崩破波。坡度倾斜度加大时,则破碎位置从顶部向下移,破碎位置在波峰中部是,则发生翻卷,表现为卷破。当坡度倾斜度很大时,则波峰根部就发生破碎。波峰根部以上的自由表面全部被零散而杂乱的浪花所取代,如图2所示。

Figure 2. The shape of wave at different slope
图2. 不同坡度下的波浪形态
3. SPH基本理论
SPH方法是一种用运动的粒子来代替流体的无网格、纯拉格朗日粒子方法。物理参数的表达式主要是通过周边区域内粒子物理参数的积分插值。基本理论如下 [11] :
3.1. 基本关系式
对于物理参数A,可以表示成关于矢量坐标
的函数,即
。函数
可以通过周边区域内相关质点的数值积分来得到:
(2)
这里,h表示光滑长度,W称为核函数,
它表示在光滑长度h为特征长度的圆圈内,众多粒子的相关参数的加权函数。在实际的数值计算中,函数
往往用离散的关系式来表示:
(3)
这里,a表示需要进行拟合函数的质点,b代表拟合函数的周边相关质点。Wab的物理意义为:a点的物理参数,需要将周边多个质点b的数值通过加权函数Wab来进行拟合。
而Wab的形式可以有很多种,这里列出几种常见的:
高斯型:
二次样条型:
三次样条型:
五次样条型:
3.2. 控制方程
光滑粒子的运动特性及相关参数的变化,可通过以下方程来进行确定:
• 连续性方程:
流体密度的变化用连续性方程表示:
(4)
这里符号
表示在a点的梯度值
• 动量方程:
动量守恒的关系可以表示为:
(5)
这里,为
对流项。常见的对流项包括人工粘性项、层流粘性和完整粘性(层流粘性 + 亚粒子湍流粘性)。
• 状态方程
这里采用形式简单的状态方程来描述水和气体:
(6)
对于水,参数
,
,分别为水的密度和声速。对于理想气体,
,B为标准大气压。
• 粒子运动方程
粒子运动轨迹遵循如下方程:
(7)
这里
,
,其物理意义为:当a点的粒子在运动过程中,它的运动轨迹与周边粒子的加权关系。
• 能量方程
内能ea可以用如下方程来表示:
(8)
这里
代表粘性项。
3.3. 边界条件
SPH中常见的边界条件有动力边界和排斥力边界。
动力边界条件的主体思想为,边界粒子和水粒子一样,满足连续方程(4)、动量方程(5)、状态方程(6)和能量方程(8),但是由于运动范围被固定,粒子运动方程(7)不满足。而排斥力边界条件则设定为边界上粒子为虚拟粒子,虚拟粒子不能被正常运动的粒子穿透,且边界粒子会给正常粒子施加排斥力。
本文所研究的对象为波浪破碎问题,该问题中,水底和斜坡的边界均与正常运动的粒子无明显的动力作用,因此这里选用排斥力边界条件。排斥力边界条件中,假设边界粒子与正常流体粒子之间的间距为r,那么排斥力
的计算方式为:
(9)
这里,
代表固体边界法向,代表R(ψ)为排斥力函数,其表达式为:
(10)
其中,
,
。c为声速。函数P(ξ)代表平行于墙运动时受到的持续的作用力:
(11)
Δb是两个相邻边界粒子之间的间距。最后,函数
则是根据水深z和速度
的修正。速度
为水质点垂直于墙的速度分量。
4. 数值算例
4.1. 概况
本文计算时的参数设定与赵津京在文献 [6] 中的水槽实验保持一致。波浪参数为周期T为2 s,水深h为0.26 m。造波方式为推板式造波,造波板的推程E为0.12 m,斜坡的倾斜角度为10˚。如图3所示。

Figure 3. The initial states of the motion of surging breaking wave
图3. 激破波运动初始状态
由于实验水槽的水深有限,这里用有限水深下色散关系来考虑波高H与波长L,具体表达式为:
(12)
这里ω为圆频率,h为水深,k为波数,
,
。根据色散关系(12)可以算出k = 0.99,即有限水深L = 6.24 m。而对应在深水下的波数k0 = 0.25,相应深水波长L0 = 24.97m。而波高H根据造波板运动幅值E与波幅A的传递函数来计算:
(13)
其中波高H = 2A,根据计算可得H约为0.066 m。深水下的波高H0与H相差不大,可根据查曲线图4来得到 [1] 。此前的波长比L/L0也可以通过图4来确定。

Figure 4. The curves of H/H0 and L/L0
图4. H/H0和L/L0的变化曲线
由于破碎点的位置不明确,这里利用(1)计算
来判断破碎的判断条件,计算得到的
约为3.43,符合激破波的发生条件。
4.2. 计算结果与实验照片的对比
本文用SPH方法模拟了激破波在爬坡过程中的破碎过程,并将计算的结果同文献 [6] 的实验结果进行了比较,对比的结果如图5所示。

Figure 5. The comparison to experiments at different time instants
图5. 不同时刻与实验的对比
从图5上可以观察到整个激破波发生破碎的全过程。在4.7 s时刻,在波浪爬坡的最高点位置,前端已开始出现较薄的一层碎浪。4.8 s开始,碎浪的范围慢慢加大,在水深很浅的前端区域,几乎全部为碎浪,到4.9 s时刻,前端的零散的碎浪依旧比较明显。但是从5.0 s开始,之前产生的碎浪重新落回水面,激破波的现象慢慢消逝。
由于部分波高转化为碎浪落回水面,此时波高已经减小,这样。从5.1 s到5.4 s,波浪的破碎形态略有转变。由于水深变浅,破碎位置更靠近岸边,此时破碎波高Hb进一步加大,参数
则减小,因此后续的运动过程和卷破波有点类似。经过一次破碎过程后的波峰,顶端延伸出去,随后直接运动至爬坡运动的最高点。此时,波峰前端已不再是零散的碎浪,而是层次分明的翻卷。
4.3. 速度矢量场
为了更好的观察破碎情况,这里计算几个时刻的矢量场。从图6的速度场可以观察到波峰前的碎浪情况。由于碎浪的具有无规律性的特点,因此在矢量图6中可以观察到碎浪速度的方向比较散乱。在4.7s时刻,波浪前端的散碎的浪花较多,且分布范围也比较广,在x = 2.1 m~2.2 m的区间内几乎都被碎浪覆盖。到了4.8 s时刻,波峰继续向岸边运动并挤压了碎浪的运动空间,碎浪的分布范围开始缩小,但是在x = 2.3 m附近仍然有少量碎浪。到5.1 s,激破波的碎浪已经不太明显,此时水质点的运动方向基本斜向上方。

Figure 6. The velocity vectors at different time instants
图6. 不同时刻的速度矢量场
4.4. 破碎位置判定
按照根据破碎的定义,最大波高受地形限制达到极限波陡时,波浪就将进行破碎。波陡定义为H/L。根据Miche提供的经验公式 [1] ,波浪在有限水深下的极限波陡有:
进行化简后,破碎波高与破碎处水深的关系大致为:Hb/Lb = 0.89。
根据图5中各个时刻激破波形态,大约在5.0 s时刻达到最大值。该时刻下,波峰前方的碎浪区域处于最活跃状态,并开始回落至水面。破碎位置可大致认定为图7中x = 1.7 m处。而破碎处的波高则可以从图7中虚线所示的水位差中大致读出。破碎位置处,从图7上可大致估算Hb = 0.105 m,而水深hb = 0.114 m。此时Hb/Lb = 0.92,与经验公式大致吻合。
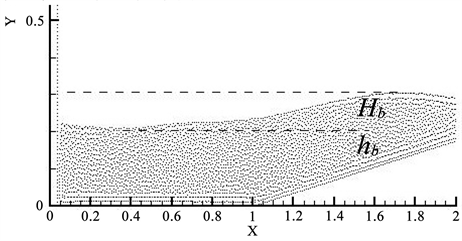
Figure 7. The wave height and water depth at the breaking instant
图7. 破碎时刻的波高与水深
5. 结论
利用SPH方法,完成了激破波爬坡的数值模拟。通过对数值模拟的结果进行观察和分析,可以得出了以下结论:
• SPH方法能较好的模拟激破波爬坡过程。爬坡过程中,波峰前的碎浪在粒子分布图上不明显,但是可以通过速度矢量图来观察碎浪的运动情况。
• 激破波的破碎过程中,波峰前出现碎浪以后的一段时候,碎浪落回水面。随后波峰会继续向前运动,波高进一步增大,在满足条件的情况下,可能出现卷破波。
• 当激破波破碎完成时,前方碎浪达到最活跃状态。此时波峰位置可视为破碎位置,破碎位置的波高可通过水位线的差值来得到。SPH结果中,破碎波高与破碎水深的比值与经验公式的比值比较接近。
虽然SPH方法能较好地模拟实验水槽的激破波运动,但是在工程实际中,激破波的运动容易受到水底地形及淤积泥沙的影响。如水底坡度变化剧烈,可将地形考虑成不同坡角组成的复合坡度 [3] ;如有较多的泥沙,可把泥沙考虑成圆形的颗粒物 [12] ,再进行数值计算或模型试验。
基金项目
国家自然科学基金资助项目(11702066);广东省自然科学基金(2017A030313275);广东海洋大学“创新强校工程”省财政资金支持项目(GDOU2016050258, GDOU2017052503)。
NOTES
*通讯作者。