1. 引言
知识经济的发展促进了技术创新,也促进了知识分布的网络化和社会化。从一定程度上来说,知识的作用就是促进技术创新。技术创新的本质也就在于新知识的创造、应用与扩散。用于技术创新的各种知识则分布于各种社会化服务机构中,如大学、科研机构与企业。因此,企业的技术创新活动离不开各种社会化服务机构的知识密集型服务(KIBS) [1]。然而,技术创新与KIBS的互动是一个复杂的非线性的知识扩散过程 [2]。
国内外众多学者纷纷展开了对知识扩散的研究,包括影响知识转移的组织因素 [3] 、知识转移对组织绩效的影响 [4] 、集群创新网络知识的动态增长 [5] 、以及促进组织间知识转移的方法和工具。最近,随着网络科学的快速增长,知识的网络化传播研究已经引起了大量的研究关注 [6]。
知识的网络化传播研究主要集中在两个方面:一是知识如何在网络中转移;二是在知识转移过程中网络本身是如何演变的。前者侧重分析网络特征对知识转移的影响,如网络关系强度对知识转移的作用 [7] 、凝聚力和范围对知识转移的影响 [8] 、网络知识转移的复杂性 [9] 、以及网络拓扑结构是对知识传播的影响 [10]。后者侧重讨论了知识转移行为对网络结构的影响机制。这些研究主要基于科学协作网络 [11] 和创新网络 [12] 展开的。随着复杂网络理论的发展,网络演化和知识转移的协同逐渐成为研究的热点。Wang和Groth提出一个衡量传播内容和社交网络之间动态双向影响的研究框架 [13]。Roth和Cointet实证检验了社会关系网络和社会语义网络的协同进化 [14]。Iñiguez等人在自适应网络上研究了科学概念的扩散,研究发现科学合理的概念比未经科学验证的概念更难普及,因为反对的人倾向形成紧密的社区,来阻止意见达成共识 [15]。
产业网络在本质上是动态的,技术创新也是动态的;因此,网络演变动力学与网络中的知识转移动力学相互交织。受到Luo等人 [16] 对社会网络上知识传播与网络结构协同演化的启发,本文以产业二分网络为研究背景,构建协同演化模型,来研究产业二分网络中“知识距离”驱动知识转移与网络结构的协同演化。
2. 产业二分网络模型
在产业二分网络中,技术创新水平影响着知识转移的局部动力学,进而决定着服务关系的嵌入。服务关系的嵌入又影响着网络结构的演化行为,形成新的网络拓扑结构;网络拓扑结构的变化又优化了知识转移路径,进一步提升了技术创新水平。图1描绘了技术创新水平、服务关系和网络结构之间的反馈环路。这种反馈环路在网络结构和结点动力学之间产生复杂的相互作用。

Figure 1. The diagram of influence of KIBS, technological innovation and industrial Bipartite network
图1. 知识密集型服务、技术创新与产业二分网络影响关系图
知识密集型服务与技术创新相互作用、相互影响,知识在企业和服务机构之间发生不断的迁移。同时企业之间、服务机构之间以及企业与服务之间的关系也不断地发生断开、重连,从而引起了网络拓扑结构的变化。
在技术创新过程中,创新企业与服务机构之间发生服务联系,表现为多对多的关系,即一个创新企业可能接受多个服务机构的服务,或者一个服务机构服务于多个创新企业。由于企业是创新的主体,即使其他企业参与了该企业的技术创新,往往也是以服务者的身份出现的,因此不妨设这些服务关系构成了产业二分网络,如图2所示。图中左侧为二分网络的邻接矩阵,黑色块表示企业与服务机构之间存在关系;图中右侧为二分网络图,显示了企业与服务机构之间的服务关系。
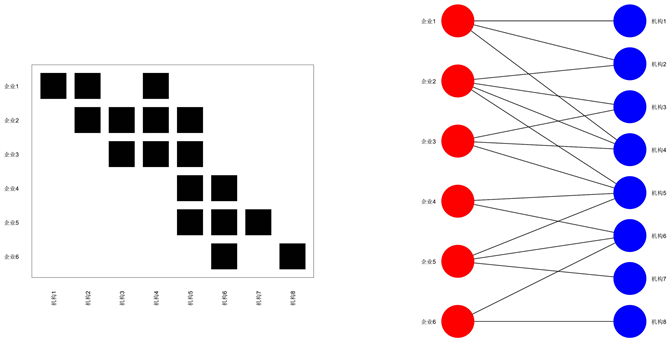
Figure 2. The diagram of industrial bipartite network based on technological innovation
图2. 基于技术创新的产业二分网络示意图
分别将二分网络向企业侧和服务机构侧投影,可以得到两个投影网络,如图3所示。
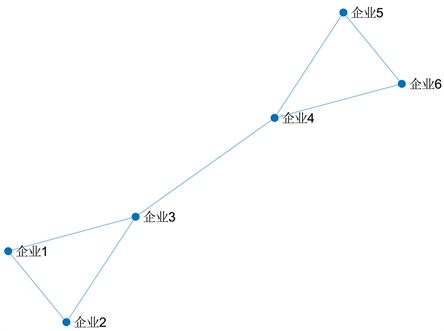

Figure 3. The projection network of industrial bipartite network (up: enterprise, down: service organization)
图3. 产业二分网络的投影网络图(上图为企业侧投影网络,下图为服务机构侧投影网络)
根据图2和图3以及下文表述的需要,本文从数学意义上给出产业二分网络的描述。假设产业二分网络中共有
个创新企业结点、
个服务机构结点、以及M条边,
。一般来说,服务关系是双向的,因此假设边是无向的,且不允许重复。分别使用
,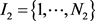 表示产业中企业和服务机构的集合,
是预先定义的企业和服务机构集合。对于企业和服务机构而言,各自都围绕技术创新拥有一些独特的“知识”。因此,对于网络结点
来说,用向量
表示其拥有的知识量,其中
表示结点i在类别k
表示产业中企业和服务机构的集合,
是预先定义的企业和服务机构集合。对于企业和服务机构而言,各自都围绕技术创新拥有一些独特的“知识”。因此,对于网络结点
来说,用向量
表示其拥有的知识量,其中
表示结点i在类别k 上的知识水平,l为知识类别总数。用
表示这个产业二分网络,E是边(服务关系)的集合。对于任何
且
,或者
且
,如果i和j之间存在服务关系(即边),则
,否则
。结点i的邻接点被定义为
或者
。
是结点j侧投影网络上的一个全连通的群组(Clique),由所有与结点i相连接的结点组成。注意,这里
并没有排除单点的情形。
上的知识水平,l为知识类别总数。用
表示这个产业二分网络,E是边(服务关系)的集合。对于任何
且
,或者
且
,如果i和j之间存在服务关系(即边),则
,否则
。结点i的邻接点被定义为
或者
。
是结点j侧投影网络上的一个全连通的群组(Clique),由所有与结点i相连接的结点组成。注意,这里
并没有排除单点的情形。
3. 基于知识距离的知识转移规则
在社会学习和协作的环境中,较大知识差距有时可能会产生沟通上的困难。例如,专家和新手之间的合作往往是无效的。Mowery等人 [17] 通过研究组织间的协作和知识转移发现,联盟中的两个组织之间存在一个最优的知识距离。
知识转移与扩散通常发生在具有不同知识水平、知识结构的组织之间,如,基础理论创新从科研院所向应用企业转移等。本文采用“知识距离(Knowledge Distance)”来表示组织知识之间的差异性与异质性特征。知识距离将影响组织间知识转移的绩效,以及组织关系的稳定性。
按照技术创新的需要,知识转移应该能够提高双方的知识水平,从而使得他们在知识转移的过程中获得收益。事实上,当双方的知识水平有一定的差距,知识转移才会发生。当然,这个差距不能太大,否则转移的知识不能被很好的学习和吸收;前面分析发现,发生知识转移的两个主体之间的“知识距离”既不是太大也不能太小,因此基于相邻结点之间恰当的“知识距离”,知识扩散才会不断发生。当知识距离大于给定的阈值时,由于缺乏常识的学习阻碍,双方没有从知识转移中获得收益。因此,假设d为“知识距离”的阈值,也是“知识交换门槛”。注意,除非特别说明,下文中的顶点表示创新企业结点或者服务机构结点。
在顶点i和顶点j之间的知识转移过程中,按照如下的步骤计算顶点i获得的知识水平:
,
(1)
其中,
,
表示知识类别。
从等式(1)可以看出,① 只有当顶点j的知识水平高于顶点i时,才能发生从顶点j到顶i的知识转移;② 当 为小于阈值d时,顶点i从顶点j获得一个有限的知识量,这个上限值由ks给出。当某类知识的知识距离小于ks时,距离越大,顶点i从知识转移中获得的收益也就越大。否则,当
超过d,顶点i就没有从知识转移中获得收益。③ 顶点i的各个类别的知识水平是逐个更新的,而且也是不断提高的。
为小于阈值d时,顶点i从顶点j获得一个有限的知识量,这个上限值由ks给出。当某类知识的知识距离小于ks时,距离越大,顶点i从知识转移中获得的收益也就越大。否则,当
超过d,顶点i就没有从知识转移中获得收益。③ 顶点i的各个类别的知识水平是逐个更新的,而且也是不断提高的。
4. 产业二分网络拓扑结构动态演化机制
知识转移和网络关系的调整同决定了产业二分网络拓扑结构的演化,同时影响了知识的局部转移。产业二分网络模型的演化按照如下的步骤进行:
Step 1:设置初始产业二分网络包括
个企业顶点、
个服务机构顶点和M条边;M条边随机分布在两类结点之间。将每个结点的知识向量初始化为随机数。
根据实际情况和研究的方便性,不妨设每个结点至少有一个链接。
Step 2:从产业二分网络中任意选择一个顶点,记为i,
(或
);
Step 3:顶点i要么以概率p与邻接点
(或
)按照等式(1)进行知识转移,要么以概率1-p调整其网络连接,使得顶点i将断开的链接重新链接到新的顶点。
Step 3.1 (链接断开):在选择与结点i断开链接的目标结点时,如果
中存在至少一个邻接点j,其与顶点i的知识距离
比阈值d大,则选择具有最大知识距离的邻接点;否则,选择具有与结点i最小知识距离的邻接点j。前者表明,当多个知识距离
大于阈值d时,说明两个结点之间的知识差距太大,无法完成知识转移,故移除服务关系;后者说明,当没有一个知识距离
大于阈值d时,说明结点之间可以进行知识转移,考虑到知识转移增益时,优先移除增益最少的一个链接,即具有最小知识距离的邻接点。
Step 3.2 (链接重连):对于上一步中断开的链接,若i是企业结点,则以概率
重新链接至
中随机选择的服务机构结点j,或以概率
链接到除
外随机选择的服务机构结点j。类似地,若i是服务机构结点,则以概率
重新链接至
中随机选择的创新企业结点j,或以概率
链接到除
外随机选择的创新企业结点j。
Step 4:更新每个顶点的知识向量和整个网络结构;
Step 5:重复步骤(2)、(3)、(4),直到迭代计数达到预先设定的上限值
。
在演化模型中,概率参数p反映了现有网络关系的粘性或者嵌入性。p值越大,网络链接粘性越大,越不容易断开,发生知识转移的可能性也就越大。
在上述模型可以看出,顶点断开链接的决策在很大程度上取决于相邻顶点之间的知识距离。因此,知识转移活动可能影响网络结构。反过来,产业二分网络的拓扑结构决定哪些顶点之间可以进行交流知识,它有对知识的扩散性能有很大的影响。
在演化过程中,创新企业或者服务机构往往倾向于删除现有的、无效的知识交流链接,并且与其他顶点建立新的联系,以寻求更好的交流机会。顶点i的网络关系调整遵循以下两个步骤:断开与重连。
步骤3.1和3.2模仿了产业二分网络中服务关系的变迁。概率
和
分别刻画了企业结点和服务机构结点在
中选择目标的倾向性。较大的参数
和
值表示本地群组(Clique)有较大的凝聚力,使个体更可能地留在本地群组,而不建立远程连接。相反,较小的参数
和
值表示本地群组(Clique)具有较小的内聚力,并且个体倾向于将服务关系“迁移”到远程位置的结点上。因此,参数
和
可以测试“社会凝聚力”或结构镶嵌对知识转移和网络结构的影响。
5. 计算实验分析
基于前面给出的协同演化模型,用计算实验的方法来分析网络结构和知识转移的协同演化。产业二分网络中有
个企业结点和
个服务机构结点。网络中的每个顶点有5个知识类别(即l = 5),对于每个知识类别,初始化为
的均匀分布。设置每次迭代的知识量上限为ks = 0.4,以及最大迭代次数为
。由产业二分网络分别向两类结点集合上投影,可以得到创新企业网络和服务机构网络。由于两个投影网络的分析过程类似,下面仅仅对产业二分网络投影后的企业网络给出实验结果和分析。
5.1. 平均知识存量的变化
网络中的平均知识存量
是网络中所有顶点在时刻t的知识平均存量,即:
(2)
从上式可以看出,
可以是直到第t个时间步时的知识转移效率,那么,
表示仿真模拟中最终达到的网络平均知识存量,可以看作是整个过程中知识转移的效率。
图4给出了网络中所有顶点的平均知识存量V和参数p和d之间的关系。可以看出,知识交换阈值d对平均知识存量V有着重要的影响:对于固定的链接粘性p,知识交换阈值d的增大,将会导致V的增大。然而,链接粘性p对V的影响非常复杂。对于固定的知识交换阈值d,当链接粘性p在一个较小的水平时,链接粘性p的增大会导致平均知识存量V的增大。然而,当链接粘性p达到一个相当大的水平时,链接粘性p的增加将不会对平均知识存量V有着显著的影响。这种现象说明,如果链路粘性非常高或非常低,那么知识转移是无效的。
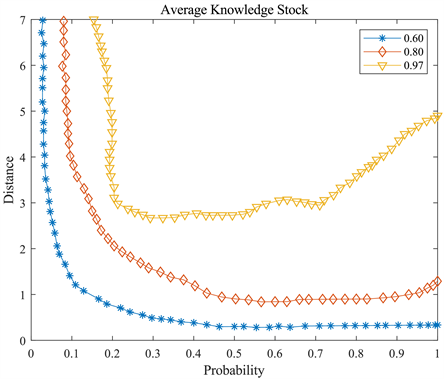
Figure 4. The relationship among average knowledge stock and link stickiness, knowledge exchange threshold in projection network
图4. 网络平均知识存量与链接粘性、知识交换阈值的关系
5.2. 知识增长速度的变化
基于网络的平均知识存量,在时刻t网络的知识增长速度为:
(3)
网络中的链接粘性p对知识扩散的影响可以通过平均知识增长速度来衡量。图5给出了网络知识增长速度
随时间t的变化曲线。

Figure 5. The rate curve of network knowledge growth
图5. 网络知识增长速度变化曲线
从图5可以看出,在早期阶段,由于各个顶点之间的知识不平衡,顶点之间的知识不断重复交换,使得知识增长的速度急剧升高;随着时间的推移,知识增长速度达到峰值。随后,由于顶点之间的知识交换不频繁,使得网络知识增长率缓慢降低。在足够长的时间后,网络顶点的知识增长速度不断降低,并趋于0,最终使得平均知识库存V处于稳定状态。
5.3. 网络结构变化
假设用最大簇系数G表示企业网络中最大簇中顶点数占全部顶点数的比例。演化结果如图6所示。在图6中,用等高线展示了最大簇系数G作为链接粘性p和知识交换阈值d的函数。可以看出,对于固定的知识交换阈值d,链路粘性p的增加将导致较大簇系数G,这是因为当链接粘性p的值较大时,边的断开与重连的倾向性较小。当知识交换阈值d增大时,最大簇系数G增大。也就是说,知识交换的阈值越小,则整个网络被分割成若干分离的小簇。与此相反,当知识交换阈值d较大时,网络中的大多数顶点相互连接,形成一个较大的群组(Clique);当阈值等于4时,整个网络是全连通的(即G = 1)。因此,网络结构的演变过程可以分为两个阶段,即“大簇”阶段和“碎裂”阶段。
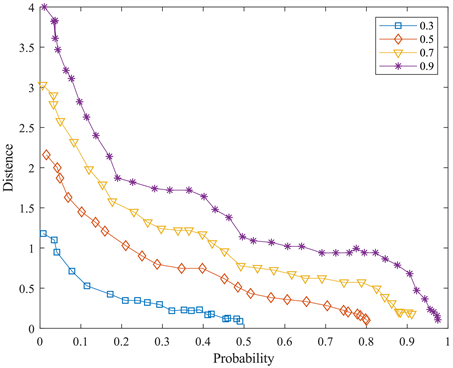
Figure 6. The relationship among maximum cluster coefficient, link stickiness, and knowledge exchange threshold
图6. 最大簇系数与链接粘性、知识交换阈值的关系
通过分析图6可以发现,知识交换阈值d对网络结构有如下的影响:当d较高时,具有较低知识距离的顶点对更可能是断开的;反之,当d较小时,具有较高知识距离的顶点对更可能被断开。因此,在较高阈值d的情况下,强连通的本地群组(Clique)倾向于瓦解。同时,一个顶点与另一个具有大的知识距离的“远程”顶点之间的链接有更多的机会来维持。整个群体趋向于形成“大簇”的阶段。同样地,在低阈值d的情况下,由于边的去除一般发生在具有很高的知识距离顶点对之间的链接上,所以强连通的本地群组更容易生存,并且整个网络更容易被分割成多个小簇。换句话说,企业网络可能落入“碎裂”阶段,每个分离的簇是由同样知识水平的顶点所构成。
通过网络的最大簇系数分析,可以发现,在演化过程中,企业网络不断碎裂与重组,呈现出连续的“小世界”拓扑结构的构建与破坏现象。图7和图8分别给出了集聚系数(Cluster Coefficient)变化曲线和平均最短路径变化曲线(其中,参数p = 0.2、d = 4)。

Figure 7. The curve of clustering coefficient C during the evolution of enterprise network
图7. 企业网络演化中集聚系数C的变化曲线

Figure 8. The curve of average shortest length during the evolution of enterprise networks
图8. 企业网络演化中平均最短路径长度变化曲线
从图7和图8可以看出,在演化初期,集聚系数C和平均路径长度l不断增加,小世界特征不显著;在平均最短路径长度到达峰值后,逐渐下降,同时集聚系数也在不断增加,网络的小世界特征越来越显著;在t = 60,000时,集聚系数C = 0.1、平均最短路径长度为l = 0.4,与同规模的随机网络相比,创新企业网络具有较大的集聚系数和较小的最短路径,因此网络逐渐自组织、并演变成一个“小世界”网络。
6. 结论
本文基于知识距离提出了知识扩散和网络结构协同演化的动态模型,通过计算实验得到了如下的结论:① 产业二分网络中的知识转移能够影响到网络结构的变化。反之,网络结构也影响知识转移的速度和效率。② 适当的“知识距离”,不但可以加快知识转移,而且能够提高网络知识存量。③ 网络知识存量随着知识扩散阈值的增大而增大,但链接粘性太高或太低都不利于网络知识存量的增加;④ 网络知识增长速度在初始阶段快速增长,而后缓慢下降到稳定状态;⑤ 产业二分网络的投影网络在演化过程中逐渐自组织形成小世界网络。
当然,本文的研究还存在如下的局限性。首先,协同演化模型中所涉及的产业二分网络是大小不变的,事实上,真实的产业二分网络的大小是在不断变化中的;其次,模型没有考虑新知识的创造。在现实世界中的知识转移总是与知识创造有关。第三,本文仅仅使用了计算实验的方法,还需要更为详细的实证检验。未来进一步的研究将在以上几个方面展开。
基金项目
国家自然科学基金项目“分层耦合区域创新网络拓扑演化与知识转移研究”(71663010);国家社会科学基金青年项目“战略性新兴产业集群生态创新机理及其生态创新政策研究”(14CJY002)。
项目来源:2017年度贵州财经大学引进人才科研项目“基于网络治理、知识转移与组织学习协同的分享技术创新研究”。