1. 引言
轴流泵具有低扬程、大流量的特点,结构简单和使用方便,在农田灌溉、核电工程市政、给排水调水工程和电厂循环水工程等方面具有广泛的应用 [1] [2] 。在轴流式叶轮设计过程中,圆周分速度修正系数的选取是重要的环节,是影响轴流泵性能的关键因素之一。
轴流泵性能研究的主要方法包括理论分析、数值模拟和实验研究。杨敬江 [3] 从理论上分析了不同轮毂比对轴流泵水力性能的影响,合理减小轮毂比可以减小摩擦损失、增加过流面积和提高叶轮抗汽蚀性能;但过分减小轮毂比会造成叶片扭曲过度,液体流动紊乱,叶轮出口处形成二次回流,导致叶轮效率下降。ZHU等 [4] 运用数值模拟的方法研究了可调导叶式轴流泵的内部流动规律,发现导叶固定会造成内部流动分离,导叶内出现涡流现象,导致水力损失增大和轴流泵的效率降低。Kang等 [5] 运用数值模拟和试验研究的方法分析了导叶叶片数对轴流泵性能的影响,发现叶片数越多,叶轮出口处轴向速度分布越均匀。石丽建等 [6] [7] [8] 通过改变叶轮的几何设计参数,采用数值模拟方法对轴流泵进行优化设计,结果表明轴流泵在非设计工况下的运行效率明显提高,拓宽了其高效区范围。何乃昌等 [9] 分析轴流泵在马鞍区工况的运行特性,对一轴流泵不同工况下的外特性进行了测量,发现扬程在马鞍区内0.55 Qd工况时达到最小值。陶然等 [10] 通过改变叶片安放角,采用遗传算法及二进制编码对轴流泵进行优化,结果表明叶片吸力面与压力面之间的压力差增大,扬程升高,水力损失的减小,轴流泵效率明显提高。Fay [11] 指出小流量工况下轮毂处的轴向速度有明显下降的现象,引起叶根侧流场状态恶化,导致轴流泵水力效率降低。
上述研究主要集中在轮毂比、叶片数、叶片安放角和叶片与导叶间距离对轴流泵水力性能的影响,但到目前为止,将速度环量作为优化轴流泵性能因素的研究还较少 [12] [13] 。本文基于圆周分速度对轴流泵进行优化设计研究,提出圆周分速度修正系数,并找到最佳的变环量设计方法。
2. 计算模型及数值模拟
2.1. 计算模型
本文采用的轴流泵模型设计流量Q = 370 L/s,扬程H = 3.3 m,比转数ns = 1250,叶轮轮缘直径300 mm,轮毂直径108 mm,叶片数为3片,导叶数为5片,转速n = 1450 r/min。
叶轮和导叶均采用流线法设计,沿径向均分成5个翼型断面(编号I、II、III、IV和V),每个翼型所在直径依次为108、156、204、252和300 mm。根据设计参数计算出5个翼型的轴向高度、翼型安放角、叶轮进出口安放角、导叶进出口安放角等叶轮导叶参数(如表1所示),然后在设计软件中快速的生成模型 [14] ,根据叶片表面光滑性,对其进行初步优化。

Table 1. Main parameters of impeller and guide vane
表1. 叶轮及导叶主要参数
表1为叶轮及导叶主要参数。其中D为翼型直径;l/t为叶栅稠密度;ηv为容积系数;vu2b为圆周分速度;Γ为速度环量;β1为叶轮进口安放角;β2为叶轮出口安放角;𝜑为翼型安放角;LZ为翼型轴向高度;ε为导叶扩散角;α1为导叶进口安放角;α2为导叶出口安放角;H为导叶高度。
将初步优化好的模型导入三维软件中进行三维建模,得到完整的轴流泵模型。计算模型如图1所示:

Figure 1. Calculation Model of axial flow pump
图1. 轴流泵计算模型
2.2. 网格划分及无关性验证
多面体网格是一种新的网格类型,为每个单元体提供了更多的毗邻单元,同时在处理变化大,复杂的几何体时,其计算精度较好,网格生产速度较快。
本次模拟网格选择多面体与棱柱层网格相结合的形式,设置边界层棱柱网格为5层,增长率为1.2,其余主流区域为多面体网格。由于模型的复杂性,在曲率半径较小的部位采用了局部加密功能。
网格的疏密度对模拟结果准确性有拟时间。一般情况下,网格越细密,其功率,扬程及效率等参数越准确,但网格细密到一定程度,计算结果显著的影响。选取合适的网格数不仅能得到优良的数值计算结果,还能一定程度上减少网格总节点数,节省模基本上趋于稳定。本文的网格无关性研究是基于相同的三维模型,相似的网格划分方法,只改变节点间距,导致网格总数的不同。通过ccm+软件对设计的轴流泵进行网格划分,分析网格数N对轴流泵效率的影响,如图2所示:

Figure 2. Relationship between grid number and efficiency
图2. 网格数和效率的关系图
由图2可知,当网格数在120万左右时,网格数的增加对轴流泵效率影响很小,可以忽略不计。因此,计算轴流泵模型时网格数应保持在120万左右最好。
2.3. 控制方程及边界条件
本次数值计算以时均N-S方程作为基本控制方程和调用标准k-ε双方程湍流模型,以基于微元中心有限体积法空间离散的方式,通过压力速度的耦合求解。
设定了两个交界面分别为interface1、interface2,即:静–动、动–静交界面,分别对应的是叶轮前端与叶轮水体交界面及叶轮水体与叶轮后端水体交界面。
进口采用速度进口边界条件,根据不同工况,给定进口流动的速度;出口采用压力出流边界条件,出口压力为101,325 Pa;壁面边界采用无滑移壁面边界条件。转子区域选用旋转坐标系,其旋转速度为叶轮转速。
2.4. 数值模拟结果分析
统计数值模拟结果可知,轴流泵的扬程为2.729 m,流量为0.37 m3/s,轴功率为12.33 KW,有效功率为9.91 KW,水力效率为80.35%。
对比该轴流泵的设计参数,发现扬程远低于设计扬程3.3 m,因此不能满足实际的工程需求。有扬程的公式(1)可得:
(1)
式中H——轴流泵扬程,单位m;
u1——进口圆周速度,单位m/s;
u2——出口圆周速度,单位m/s;
vu1——进口圆周分速度,单位m/s;
vu2——出口圆周分速度,单位m/s;
g——重力加速度,单位m/s2。
(2)
式中:u2——出口圆周速度,单位m/s;
D——叶轮外径,单位m;
n——叶轮的转速,单位r/min。
由式(2)可得圆周速度u2跟叶轮直径D和转速n有关,一般叶轮外径D和转速n是确定的,因此圆周速度u2保持不变。在式(1)中圆周分速度vu1由吸入条件决定,通常vu1 = 0,重力加速度g是定值(一般取9.81),可以分析得到扬程H主要跟出口圆周分速度vu2有关。因此扬程H偏小主要是由出口圆周分速度vu2偏小所导致的。
以翼型所在的直径作相应的圆柱面,在叶片出口边位置取一平面,与圆柱面相交一段圆弧,在两个叶片出口边对应的圆弧上平均取10个点,如图3所示。10个点作为模拟圆周分速度的测量点,分别统计每个测量点的圆周分速度,进而计算出每个翼型的平均出口圆周分速度。5个翼型模拟的圆周分速度分布图如图4所示:
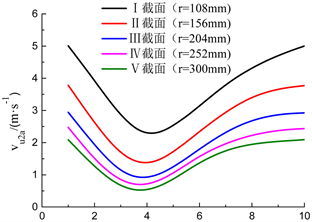
Figure 4. The distribution of the circumferential velocity of the original model
图4. 原模型圆周分速度分布图
分析可得,5个翼型截面的平均模拟圆周分速度变化趋势大致相同,呈现先减小后增大趋势;从轮毂到轮缘,圆周分速度依次减小,且越靠近轮毂处速度变化的趋势越明显,越靠近轮缘处速度变化的趋势越平缓。
表2为圆周分速度对比表。其中模型模拟圆周分速度表示为vu2a;设计圆周分速度表示为vu2b。

Table 2. Circular velocity comparison table
表2. 圆周分速度对比表
由表可得:模拟得到的圆周分速度明显小于设计的圆周分速度,误差平均为22.87%。
vu2是液体在出口处绝对速度的圆周分速度。根据轴流泵出口处速度三角形分析,如图5所示:
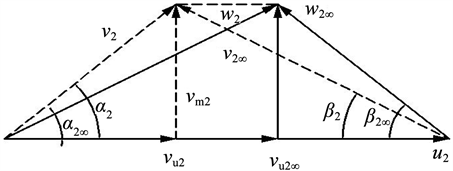
Figure 5. Velocity triangle at blade outlet
图5. 叶片出口处速度三角形
分析可得:在轴流泵设计过程中,是以无限叶片数假定的,但实际叶片数是有限的。液体在有限叶片数叶轮和无限叶片数叶轮中流动状态差别很大,因此需加入圆周分速度修正系数ε来修正圆周分速度。
3. 轴流泵优化分析
3.1. 圆周分速度修正系数的选取
为了满足设计扬程要求,需增大圆周分速度,即增大圆周分速度修正系数。取5组不同的圆周分速度修正系数,分别为1.1、1.2、1.3、1.4和1.5 (假设采用等环量设计,即5个翼型的圆周分速度修正系数取值相同)。圆周分速度的变化直接影响叶轮出口安放角以及导叶进口安放角的大小,因此圆周分速度修正系数改变,叶轮出口安放角和导叶进口安放角也随之改变。三维建模,数值模拟,统计圆周分速度(每组测量点的平均圆周分速度)的分布规律。5组模型圆周分速度对比图如图6所示。
分析可得:5组曲线的变化趋势大致相同,圆周分速度修正系数越大,其圆周分速度值越大。对比设计的圆周分速度,ε = 1.4的5组翼型圆周分速度最接近,分别相差3%、5%、2%、4%和2%。
外特性统计结果如表3所示,表中ε为圆周分速度修正系数,H为扬程,P为轴功率,η为水力效率。
根据表3结果可知,在轮毂比和流量不变的情况下,随着圆周分速度修正系数变大,轴流泵的扬程随之升高,轴功率也随之增大;而轴流泵的效率先升高后降低。当圆周分速度修正系数达到1.3时,效率最高为82.07%。但其扬程不满足设计扬程需求,应取圆周分速度修正系数为1.4,其效率为81.94%。

Table 3. Comparison table of 5 groups of circumferential velocity results
表3. 5组圆周分速度结果对比表
3.2. 优化设计
在满足设计扬程情况下,翼型的圆周分速度修正系数选取1.4,但实际的设计过程中,叶轮设计采用变环量设计,即5个翼型的圆周分速度修正系数不尽相同。以ε = 1.4为基准,设计4种优化方案,4种优化方案采用了4种不同的变环量设计。方案1是轮毂到轮缘圆周分速度修正系数线性增大;方案2是轮毂到轮缘圆周分速度修正系数线性减小;方案3是中间翼型断面圆周分速度修正系数较大,而轮毂和轮缘处圆周分速度修正系数较小;方案4是中间翼型断面圆周分速度修正系数较小,而轮毂和轮缘处圆周分速度修正系数较大。如表4所示:
图7为优化方案速度环量对比图,可以看出:5种方案速度环量分布规律大致相同,中间翼型速度环量较大,轮毂轮缘处速度环量较小。方案2的平均速度环量最大,原方案的平均速度环量最小。方案1和方案3速度环量极差较小,分布比较平均;方案2速度环量极差最大。

Figure 7. Optimization scheme speed loop comparison diagram
图7. 优化方案速度环量对比图
图8为4种优化方案叶片出口边轮毂处速度矢量图,可以看出:方案1没出现旋涡等不良流态,流态稳定,流速分布均匀;方案2叶片压力面轮毂处有明显的旋涡,流态紊乱;方案3和方案4出现小旋涡,对流态影响较小。

Figure 8. Velocity vector diagram at blade outlet hub
图8. 叶片出口边轮毂处速度矢量图
图9为4种优化方案叶片吸力面流线图,可以看出:方案2叶片吸力面产生明显的旋涡和脱流现象,出口边流线不顺滑;方案1叶片吸力面流线相对均匀;方案3和方案4有轻微的脱流现象。

Figure 9. Suction streamline diagram of blade
图9. 叶片吸力面流线图
图10为优化方案1内部流线分布图。进一步展示优化方案1内部流动状态,从图中可以看出,叶轮和导叶处无明显的回流和旋涡,流态稳定均匀,流线分布合理。
由表5外特性结果分析可得:以上方案均满足设计扬程,方案2和方案4轴流泵效率低于原方案,优化设计不合理;方案3轴流泵效率稍微大于原方案,优化效果不明显;方案1的效率比原方案提高了0.75%,故采用方案1作为优化设计方案。

Table 5. Optimization scheme external characteristic result table
表5. 优化方案外特性结果表
综上:变环量设计中,应减小轮毂处的环量,同时增大轮缘处的环量,可改善叶片扭曲度过大的情况,减少脱流和旋涡等不良流态,一定程度可以提高轴流泵的水力性能。
3.3. 优化结果分析
原模型优化后,叶轮的几何形状发生了明显变化,这是轴流泵水力性能提高的根本原因。优化后,叶片轮毂处进口安放角为38.8˚,叶片轮毂处出口安放角为74.3˚,叶片轮缘处进口安放角为16.9˚,叶片轮缘处出口安放角为18.8˚,叶片轮毂处包角为56.8˚,叶片轮缘处包角为73.1˚。
图11为轴流泵优化前后的水力性能对比图,分析可得:在设计工况下,扬程从2.729 m提高到3.44 m,水力效率从80.35%提高到82.69%,均满足设计要求。优化模型高效区明显扩大,表明优化模型在多工况下的水力性能得到了提升。
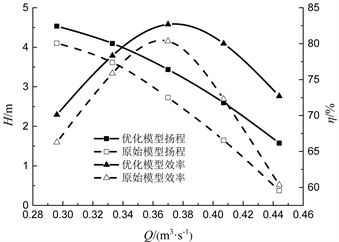
Figure 11. Comparison of original and optimized performances
图11. 优化前后轴流泵水力性能对比
4. 结论
通过数值模拟分析,基于圆周分速度对轴流泵优化设计研究,得到以下结论:
1) 通过解决轴流泵实际扬程偏低的问题,提出了圆周分速度修正系数。针对ns = 1250的轴流泵,最佳圆周分速度修正系数以1.4为基准,同时采用变环量设计,减小轮毂处的环量,增大轮缘处的环量。
2) 数值模拟可有效验证优化设计的结果。优化后,叶轮内部流态更加平稳,增强了叶片的做功能力,扩大了轴流泵的高效区;在设计工况下,扬程从2.729 m提高到3.44 m,水力效率从80.35%提高到82.69%,均满足设计要求。
参考文献