1. 引言
气体轴承是利用压缩空气作为润滑介质,通过工期压力的悬浮作用,产生气体轴承旋转轴和固定基座的分离,为此静压气体轴承有较高的旋转速度,有较小的摩擦力矩,无污染等优点。同时对于分析气体静压轴承的流场变化也随着计算机性能的提高和计算软件的日益丰富,对气体轴承的分析也越来越成为研究的重点 [1] [2] 。
目前对静压气体轴承的理论计算和仿真研究中大多停留在承载特性以及运动性能方面,较少的对流场内部变化对节流小孔静压轴承影响的研究。在仿真计算过程中于贺春 [3] 得出了动压对气体静压轴承的影响不可忽略;黄首峰 [4] 通过建立滑动轴承得出了油膜压力等变化情况;胡俊宏 [5] 得出了存在最佳气膜使得承载力最大;孙雅洲 [6] 和饶河清 [7] 通过分析多空介质静压气体轴承承载能力和压力分布情况;Renn [8] 通过实验和模拟分析,提出了新的节流孔结构形式有利于对静压轴承设计和建模;Eleshaky [9] 捕捉流场的相干结构在轴承入口区域包括凝聚成的冲击波和压缩波区激波/边界层相互作用(伪冲击)。Gao [10] 得到了不同的节流孔形状对气体止推轴承影响很大;李运堂 [11] 通过大涡模拟分析了止推轴承的振动特性。
利用三维模型软件,建立三维实体静压轴承的流体域模型,通过有限元软件对三维模型进行网格划分,然后通过选择求解模型对求解Naver-Stokes方程下的静压气体轴承进行仿真计算,主要是围绕节流孔附近区域流场变化大的特点,进行流场参数变化分析,通过数据变化情况,得出静压气体轴承由于流场影响所产生的振动问题。
2. 基本方程
利用LES模型主要是为了解决大涡在湍流时,流场内漩涡尺度小于网格间距的问题。控制方程采用的是随时间变化的Navier-Stokes方程,包括连续性方程和动量方程:
(1)
(3)
方程(1)是质量守恒方程,(2)是动量守恒方程,其中uij是代表在笛卡尔坐标系中的速度方向,xi和xj是代表在坐标系中的方向向量,δij是粘性应力张量。
(3)
(3)是能量守恒方程
大动荡的漩涡可以运用亚网格尺度应力模型求解计算。(1)和(2)中的计算公式是小于网格大小的湍流模型。作为亚网格尺度模型,适应当地的涡流粘度壁模型,本文利用有限体积法在CFD软件FLUENT中进行了LES模拟。
通过隐式求解压力(PISO)算法作为压力速度耦合计算的方法。为减小数值耗散,选择了二阶迎风插值法求解密度、湍流动能和湍流耗散率,而选择有界中心差分法用于LES中的动量插值。作为瞬态公式,采用二阶隐式格式。时间步长
s
3. CFD仿真
3.1. 建立模型
基本结构参数,轴承直径D = 30 mm,长度L = 30 mm,气膜厚度h = 20 μm,节流孔到轴承两端距离l = 7.5 mm,节流孔直径d0 = 0.2 mm,截流腔直径d1 = 0.8 mm,深度h1 = 0.1 mm,利用Gambit建立气体轴承流体区域的三维模型,如图1所示,同时通过自定设置偏心率,其中偏心是沿着90˚节流孔方向,建立不同偏心率下的气体轴承模型,通过建立不同偏心率的气体轴承流体域的三维模型进行数值模拟计算分析。

Figure 1. The model of gas basin and the position of throttle hole
图1. 气体流域模型及节流孔位置
3.2. 网格划分
在模型建立完后对模型进行网格划分,由于气膜区域内的间隙很小,同时轴承是属于旋转体,所以整个网格的扭曲率较大;同时由于在气膜区域的结构变化较大,因此导致流场变化也很大,为了整体达到比较好的网格质量和FLUENT求解计算中更加容易收敛,需要在流速变化较大的区域进行网格划分时进行网格加密,如图2(a)中,对流速变化较大的小孔节流区域需要进行局部网格加密,同时对模型需要进行分块划分网格划分处理,将模型分为10个主要区域如图2(b),使远离节流孔处的区域能划出规则的八面体网格。
3.3. 边界条件及初始化
将设定进气边界条件(pressure-inle)和出口边界条件(pressure-out),进口边界设定在每个进气孔的外表面,压力出口边界条件为气体轴承轴向方向两端的气膜间隙面,同时定义气膜区域内的表面为壁面(wall)。
 (a) 定义节流孔附近条件和监测点
(a) 定义节流孔附近条件和监测点  (b) 节流孔在轴承的位置
(b) 节流孔在轴承的位置
Figure 2. Definition of the conditions near the throttle and the monitoring point
图2. 定义节流孔附近条件以及监测点
3.4. 求解计算
在计算的过程中,设立进口压力为6个大气压,压力出口边界条件为1个大气压,设立常温为工作温度。空气粘度系数为1.84 × 10−5 η (pa∙s),为了更加准确的得到LES模型结果,将LES计算建立在稳态计算的基础上,将稳态计算选用可保存雷诺应力与湍流一致的Realizable K-ε型。
4. 计算结果分析
图3是在圆周90˚位置节流孔附近三个相邻时刻的涡量云图和涡线图,可以看出涡量的主要是分布在靠近节流孔附近的环形区域,在逐渐远离节流孔的位置上涡量逐渐减少,流场逐渐变成层流和均匀,同时从三个不同时刻进行对比,可以看出,涡的形成和变化的大致过程,在这个过程中看出t1时速度而变化,也最终由于气膜间隙中的压力差引起了一定的振荡。

Figure 3. Eccentricity (ε = 0.3) position distribution at 90˚
图3. 偏心率(ε = 0.3)位置分布在90˚
图4是位于周向306˚处的节流孔附近位置的涡量和涡线图,图4的涡量与图3的变化基本相同,在这个过程中仍然是出现了涡的聚集和涡的分离,随着位移的发生,涡的强度逐渐衰减至流场区域层流状态。但是与图3相比,整个过程存在不同,图4中的涡相对图3可以看出,涡的个数变少了,同时涡的强度变小了,涡的发散程度变大,流场的整体区域相对于图3的情况变化较小,这是由于轴发生了偏心位移,306˚位置的气膜厚度比90˚位置的气膜厚度要厚很多,所以在306˚附近的节流孔区域的流体区域变大,导致了整个区域的流阻变小,对流场内的流体的速度阻碍作用减少,形成的涡量也变小,同时由于气体的压缩性所导致,引起气流在较大间隙处的振荡较为明显;所以相对90˚位置区域,306˚区域内的涡量变化较小,从而由于涡的形成和分离带来的振荡较小。

Figure 4. Eccentricity (ε = 0.3) position distribution at 306˚
图4. 偏心率(ε = 0.3)位置分布在306˚
图5是三个节流孔附近区域监测点point-1流场的参数变化图,图5(a)是流场中压力随时间变化的曲线图,由于90˚处的气膜厚度最小,则压力最大,306˚的气膜厚度最大,则压力最小,同时可以看出在整个模拟计算时间中,压力都是先突然增大然后处于相对平稳的波动过程,在这个平稳的波动过程中压力出现了一定幅度的波动,这也说明在图3,图4中涡的聚集和分离导致的压力出现一定波动的一部分原因。图5(b)是监测点point-1处的速度曲线随着时间变化的曲线图,在图中可以看出,速度曲线变化也是和图5(a)有一定的波动性,对比图5(a)可以看出,速度变化的波动性和压力波动性呈现出一定的反比例关系,当压力降低的前期过程中,速度是有所增加,当后期压力出现小幅度的减小时,速度出现了增加的现象,图5(c)是涡量随着时间变化的曲线图,306˚处的涡量变化幅度较大,在18˚处涡量变化幅度较小,由于气膜厚度的不同,在气膜间隙较大的306˚处中,由于间隙的变大,导致了流阻变小,从而导致了速度梯度变化较大,所以涡的存在主要是间隙较大的地方。图5(d)是马赫数随着时间变化的曲线图,马赫数的变化情况和图5(b)中速度变化曲线的变化趋势基本相同,同时不同位置处的马赫数在气膜间隙较大处的306˚是最大的。
图6是306˚节流孔附近区域三个不同的监测点的压力,速度,涡量以及马赫数随时间的变化曲线图,图6(a)是三个监测点的压力随时间变化的曲线图,在图中可以看出靠近节流孔处的point-1压力是三个监测点中最大的,同时可以看出point-3的压力是要高于point-2的压力,这说明随着远离节流孔的位移上,压力出现了先变小后增大的过程,同时point-2和point-3处的压力波动较point-1的波动较小,图6(b)是三个监测点速度变化曲线图,在三个速度变化曲线图中,我们可以看出point-2和point-3速度波动大于point-1的速度波动,于图4和图5得出的结论,可以看出在远离节流孔的位移上涡量变化较为明显,图6(c)是三个监测点的涡量变化情况,point-2和point-3两个点的涡量波动明显要大于point-1的涡量波动,这也说明了从图6(a)和图6(b)得出结论的正确性和合理性,图6(d)是三个监测点的马赫数变化情况,与图6(d)的变化情况一样,同时可以看出在整个变化过程中,马赫数都未超过1,与图5(b)相比,可以知道马赫数最大的区域是在节流区域的下表边缘。
 (a)
(a)  (b)
(b) 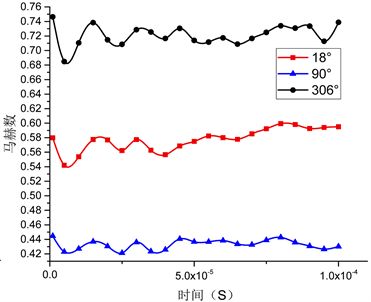 (c)
(c) 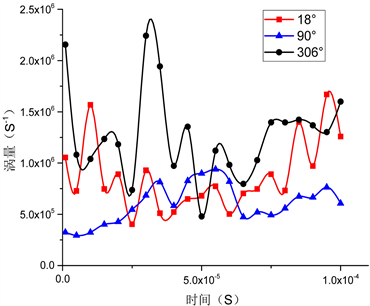 (d)
(d)
Figure 5. The change of pressure, velocity and Maher number with time at the monitoring point at different throttle points at point-1
图5. 不同节流处监测点point-1处压力,速度以及马赫数随时间的变化图
5. 结论
本文研究小孔节流静压气体轴承的瞬态流动特性。为了捕捉湍流结构和波动,采用LES方法数值计算轴承间隙内的瞬态流场。分析了轴承间隙中压力、速度、马赫数之间的波动以及涡结构。讨论了气体静压轴承的压力波动和振动特性。从本文的研究结果可以得出以下结论:
 (a)
(a) 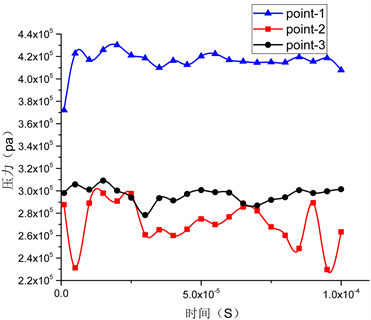 (b)
(b) 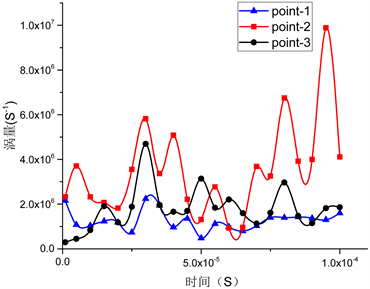 (c)
(c)  (d)
(d)
Figure 6. The change of pressure, velocity, vorticity and Maher number at point 3 point at 306˚
图6. 306˚处点3监测点的压力,速度,涡量以及马赫数变化
1) 旋涡在空气静压轴承的节流腔中不断产生和脱落,在气膜间隙较大的位置漩涡强度较大,数量较小,在气膜厚度较小的位置,涡的数量较多,但强度较小。
2) 涡的产生和脱落都伴随着压力的波动,而速度的与压力的变化存在近似反比的关系。气膜厚度越大马赫数越大。
3) 越靠近节流孔的位置速度越大,马赫数也越大。
基金项目
国家自然科学基金(11562002);广西自然基金(2015GXNSFAA139262);广西研究生创新项目(GKYC201704)。