1. 引言
记
为复平面上的单位开圆盘,
表示开圆盘的边界,
表示正规的面积测度。Sobolev空间
是由单位开圆盘
上满足
的函数
构成的空间,且空间
在内积
下构成Hilbert空间。
Bergman空间
是由
中所有解析函数构成的空间。
是Hilbert空间,其内积规定为
。Dirichlet空间
是由Sobolev空间
中导数属于
且在原点取值为0的解析函数构成的空间。因此
也是Hilbert空间,内积为
。
Douglas在文 [1] 中讨论了Hardy空间上Teoplitz算子的交换性。此外,Zhu & Zheng [2] 主要刻画了Hardy空间和Bergman空间上的空间理论和算子理论。由于Dirichlet空间是由函数导数来定义的,因此其性质结构与经典的Hardy空间,Bergman空间有着许多的不同之处。Cao [3] 讨论了Dirichlet空间上Toeplitz算子的Fredholm性质及本质谱。Duistermaat [4] 讨论了带调和符号的Toeplitz算子的交换性。Yu [5] 刻画了Dirichlet空间的Toeplitz算子是紧的当且仅当此算子为零算子。在 [6] 中,Chartrand主要研究了Hardy型、Bergman型算子的有界性问题。
本文主要讨论了Dirichlet空间上Hardy型Toeplitz算子的半交换性、紧性、Fredholm性质和本质谱。
2. 预备知识
我们知道空间
(Hardy空间)。令
表示从
到
上的正交投影。如果边界
上的函数
满足
,则我们可以定义从
到
的Toeplitz算子为
, (1)
其中
,
且
表示Szegö投影的核。
记调和函数
,
其中
,
是解析函数。记正整数集为
,由于
是空间
的标准正交基,所以
,
。从而
。
令
表示
的Poisson积分。如果
,
,则
,
。
设
是边界
上的有界调和函数,令
。若
满足
,那么Toeplitz算子
可以定义在空间
上。因为
,
且
和
正交,则此算子
在空间
上是有界的。
3. 紧性和半交换性
我们称
是可导的指的是它到圆盘内部的Possion扩张是可导的。为了方便,这种意义下,我们不再区分
和它的Possion扩张。一般地, 。在 [7] 中,我们讨论了
的充要条件是
为常值。
。在 [7] 中,我们讨论了
的充要条件是
为常值。
定理3.1:设
。如果
,则
是紧算子当且仅当
是共轭解析的。
证明:对
,我们有
。
不失一般性,令
,
,则
在
上弱收敛到0。从而
。
对固定的
,总有
。因此,我们有
。
于是,若
是紧算子,则
。因此,由Cauchy-Schwarz不等式知
。进一步地,我们有
。又因为系数
(自然数),故必要条件得证。反之,显然。证毕。
定理3.2:如果
,则
紧当且仅当
。
证明:显然,如果
,则
是紧的。若
紧,令
,则
,
,
。因为
,于是由(1)知,
。
又
,则
。
因此,对
,
,当
时有
。固定
,对
,我们有
,于是
,即
。又因为
,从而当
时,系数
可以取遍整数集。故
,进而
。证毕。
接下来,我们考虑两个算子的乘积的紧性问题。假设
。
定理3.3:如果
,则
是紧算子当且仅当
共轭解析或
是多项式。
证明:对
,我们有
,
。
此外,
, (2)
, (3)
, (4)
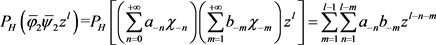 。 (5)
。 (5)
记
,则由等式(2),(3),(4)和(5)知,
。 (6)
由于
在空间
中是弱收敛到0的,从而如果
是紧算子,则对
,
,当
时有
。
令
,则
。 (7)
由(7)有,
。因此对整数
,我们有
。
于是对整数
有
,即
或
(整数
)。从而,如果
是紧算子,则
共轭解析或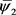 是多项式。
是多项式。
反之,由于
是空间
的标准正交基和等式(6),则充分条件是显然的。证毕。
注:对
,我们不能保证
。一般地,
,但是
在空间
上却是有意义的。
推论3.4:如果
且
不是多项式,则
当且仅当
是共轭解析的。
证明:对
,记
,
。若
,则
,从而
。
进一步,我们有
。
于是当
时,总存在某个
,满足
。因此,由定理3.3可知,
是共轭解析的。反之,显然。证毕。
定理3.5:如果
,则
是紧算子当且仅当下列条件中的一个成立:
1)
或
共轭解析;
2)
,
都是多项式。
证明:通过计算,我们有
。
同时,
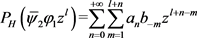 ,
,
,
,
。 (8)
记
。我们已经得到了(2),(3),为了计算
,我们还需要计算
。事实上,
。此外,由于等式(3)和(8)是相等的,因此
。
从而,
。 (9)
如果
是紧算子,则
。对
以及固定的
,
当且仅当
,
同时成立。故
和
同时成立,从而得到必要条件。反之,由等式(9)易得。证毕。
4. 本质谱
事实上,对Toeplitz算子
而言,我们有
,从而
。此外,如果
为Fredholm算子,则
,其中
表示
的本质谱。自然地,我们想得到本质谱和谱之间的关系。为了达到这个目的,我们还需要以下引理。
引理4.1:设
,则
。
证明:令
。由
,则
。
从而
 。 (10)
。 (10)
由于
,
则
。 (11)
另外,由于
,
则
。 (12)
故由(10),(11)和(12)得,
。证毕。
定理4.2:设 ,则
。
,则
。
证明:我们只需要证明
。如果
,则存在
使得
。令
,则在空间
上有
。由于函数
在
处取得最大值,则对
,我们有
。
又
,
,因此由引理4.1知,
。从而
不可能是一个Fredholm算子,因此
。证毕。
推论4.3:设
。如果
是一个Fredholm算子,则
。
证明:如果
是一个Fredholm算子,则
。由定理4.2知,
,故
。证毕。
基金项目
国家自然科学基金(NO. 11501068),重庆市教委科研项目(NO. KJ1600302)。