辽宁省电力景气先行指数与用电需求相关性研究

Study on Correlation between Electric Power Boom Index and Electricity Demand in Liaoning Province

摘要: 为检验辽宁省电力景气先行指数是否对其用电需求具有预测作用，能否达到实现从经济看电力的功能。本文首先以X-12-ARIMA季节调整法作为景气指标数据处理方法，并以时差相关分析法划分辽宁省电力景气指标，而后采用基于主成分分析法的合成指数方法编制辽宁省电力景气先行指数，并分析其波动情况。在此基础之上，将辽宁省电力景气先行指数与辽宁省全社会用电量进行相关性分析，通过构建向量自回归(VAR)模型、脉冲响应函数以及方差分解等方法检验电力景气先行指数与辽宁全社会用电量之间的相关性。检验结果表明，辽宁省电力景气先行指数是辽宁省全社会用电量的格兰杰原因，并且二者之间存在稳定关系，即电力景气先行指数可以起到预测辽宁省未来电力需求总体状况的作用。

Abstract: In order to test whether the Liaoning Province Power Climate Pioneer Index has a predictive effect on its electricity demand and whether it can achieve the function of realizing electricity from the economy, in this paper, the X-12-ARIMA seasonal adjustment method is firstly used as the data processing method for the prosperity index, and the power climate index of Liaoning Province is divided by the time difference correlation analysis method. Then the synthetic index method based on principal component analysis is used to compile the Liaoning Province power boom index. And its fluctuations are analyzed. On this basis, the correlation between Liaoning Province's power boom index and Liaoning’s total social power consumption is analyzed, the correlation between the electric power boom leading index and the electricity consumption of the whole society in Liaoning Province is tested by constructing the vector autoregressive (VAR) model, impulse response function and variance decomposition. The test results show that the Liaoning Power Boom Pioneer Index is the Granger cause of the whole society’s electricity consumption in Liaoning Province, and there is a stable relationship between the two. That is, the power boom leading index can play a role in predicting the overall situation of future power demand in Liaoning Province.

1. 引言

电力工业在国民经济发展中占有举足轻重的地位，它是国民经济的支柱、基础和命脉产业，也是国民经济发展水平的具体体现。电力生产及供给的稳定可靠为我国经济高速发展、社会持续进步和人民生活水平提高提供了必不可少的基础条件 [1] ，而电力供应短缺则将制约经济规模发展、阻碍产业结构调整，同时影响工农业生产和人民生活水平。因此，随着国民经济的不断发展，电力作为国民基础性能源，其稳定可靠性诉求也在不断提高，关于电力需求预测的研究也愈发成为热点和关键点。

而辽宁省作为我国最重要的工业城市之一，其经济发展与电力的关系更是密不可分。因此，加强电力及相关数据分析，预测辽宁省未来用电需求趋势便显得尤为重要。

2. 辽宁省电力景气先行指数

2.1. 辽宁省电力景气指标的筛选

为构建科学有效的辽宁省电力景气先行指数，本文以经济重要性、统计充分性、敏感性、实效性和准确性为景气指标选取原则，筛选出辽宁电力景气指标，并运用目前使用最广泛的X-12-ARIMA季节调整法对指标数据进行预处理，提高数据的准确性。

在通过对各种常用的景气指标选取方法进行分析与比较后，结合辽宁省电力景气指标的特点，选取时差相关分析法作为辽宁省电力景气指标的筛选方法，得出辽宁省GDP、辽宁居民人均可支配收入和辽宁制造业用电量三个指标的先行期数分别为−3、−3、−7，可以被确认为辽宁省电力景气指标的先行指标。

2.2. 辽宁省电力景气先行指数的编制

在进行电力景气指标划分的基础上，便要进行电力景气指数的编制。通过分析景气指数的编制方法，本文选择基于主成分分析法的合成指数方法编制辽宁电力景气合成指数。

选取前文所界定的先行指标组，即辽宁省GDP、辽宁居民人均可支配收入和辽宁制造业用电量，三个指标来计算先行合成指数。应用SPSS软件中“Analyze->Data Reduction->Factor”命令，用主成分分析法，得到辽宁电力景气先行指标公因子成分如表1所示。

Table 1. Preliminary indicator factor composition table

表1. 先行指标因子成分表

从上面成分矩阵可以看到，设为L第一主成分， $x_1,x_2,x_3$ 分别表示辽宁GDP、辽宁居民人均可支配收入和辽宁制造业用电量，则有：

$L=0.784x_1-0.803x_2+0.727x_3$ (4-19)

通过公式可以计算辽宁电力景气先行合成指数，如表2所示。

Table 2. Liaoning power boom first synthetic index table

表2. 辽宁电力景气先行合成指数表

通过计算电力景气先行合成指数，可以反映辽宁电力景气的整体变化趋势和波动程度，为有关部门的超前判断电力市场的供需状况提供科学依据。辽宁电力景气先行合成指数波动情况如图1所示。

3. 辽宁省电力景气先行指数波动分析

2013年第一季度至2017年第四季度期间，辽宁电力景气先行指数在每年的第一季度均达到该年景气指数最低值，即波谷；均在第二季度达到景气指数的最大值，即波峰；每年第三季度、第四季度的电力景气指数较为接近，除2016年第四季度先行指数较同年第三季度指数有较大下滑之外，其余年份第四季度较第三季度的指数均呈小幅下降趋势。虽然2017年景气先行指数波动状态出现偏差，即同比往年波峰2017年波峰指数降幅较大，但考虑到2017年其它季度的景气先行指数同比往年有较大幅度的升高，并且由于2013年至2016年期间，每年先行指数波峰均略高于前一年波峰，2013年至2017年期间，指数波谷于2015年达到最低值后开始呈现上升趋势，因此辽宁电力景气先行合成指数总体仍呈现出一种缓慢稳步攀升的态势。

Figure 1. Liaoning power boom first synthetic index fluctuation chart

图1. 辽宁电力景气先行合成指数波动图

不难看出辽宁电力景气指数存在周期波动。这种周期性的波动可以体现出季节性因素对用电需求的影响，例如电力景气指数会在第二季度(夏季)处于较高水平。而另一方面，景气指数在个别年份或季度会出现波动偏差，这可能是由于宏观经济或其它因素导致，例如受到煤炭价格上涨影响，导致发电企业成本上升，使得辽宁电力景气指数波动发生变化。

4. 电力景气先行指数与用电需求相关性分析

由于辽宁电力景气指数的基准指标为辽宁全社会用电量，即电力景气一致合成指数与辽宁全社会用电量保持一致。而全社会用电量能够在很大程度上反映一个地区电力景气的真实状况 [2] ，因此为了进一步检验辽宁电力景气先行合成指数是否对辽宁省电力需求具有预测指导功能，本文将对辽宁电力景气先行合成指数与辽宁省全社会用电量数据进行拟合，如图2所示。

Figure 2. Liaoning power boom first index and the whole society electricity consumption fitting chart

图2. 辽宁电力景气先行指数与全社会用电量拟合图

可见，辽宁省电力景气先行合成指数可提前预测辽宁全社会用电量的走势。为进一步检验电力景气先行指数对辽宁全社会用电需求的预测功能，本文将对辽宁电力景气先行合成指数与辽宁全社会用电量进行相关性分析。

4.1. 向量自回归(VAR)模型的建立

考虑到叙述的简便性，下述的向量自回归模型都是不含外生变量的非限制性向量自回归模型，用下面的数学式子表示为 [3] ：

$y_t=A_1{y}_{t-1}+A_2{y}_{t-2}+\cdots +A_p{y}_{t-p}+B{x}_t+{\mu }_t$ ，或者是 $A\left(L\right)y_t={\mu }_t$ ， $t=1,2,3,\cdots ,T$ (5-5)

若行列式det[A(L)]的跟斗在单位圆的外部，则上述式子满足可逆性的条件，可以将其表示为无穷阶的向量移动平均(VMA(∞))的形式：

$y_t=C\left(L\right){\mu }_t$ (5-6)

其中， $C\left(L\right)=A{\left(L\right)}^{-1}$ ， $C\left(L\right)=C_0+C_{1}L+C_2{L}^2+\cdots$ ， $C_0=I_k$ 。

对向量自回归模型的估计可以采用最小二乘法，假设对求和矩阵不施加任何的限制性条件，根据最小二乘法可以得到求和的估计量为：

$\Sigma =\frac{1}{T}{{\displaystyle \sum }}^{\text{}}{\hat{\mu }}_t{{\hat{\mu }}^{\prime }}_t$ (5-7)

其中， ${\hat{\mu }}_t=y_t-A_1{y}_{t-1}-A_2{y}_{t-2}-\cdots -A_p{y}_{t-p}$ ，当向量自回归模型的参数估计出来之后，由于 $C\left(L\right)A\left(L\right)=I_k$ ，

因此，可以得出相应的VMA(∞)模型的参数估计结果。

滞后阶数的确定是VAR模型中一个重要的问题。本文选取AIC和SC信息准则确定最佳之后期。其计算方法如下：

$AIC=-\frac{2l}{T}+2n/T$ , $SC=-\frac{2l}{T}+n\ln T/T$ (5-8)

其中，在VAR模型中 $n=k\left(d+p\times k\right)$ 是被估计的参数的总数，k是内生变量个数，T是样本长度，d是外生变量个数，p是滞后阶数，l是对数似然值 [4] 。

在进行模型滞后阶数的选择时，AIC值越小越好，可以通过选择最小值来确定一个滞后分布的长度。而SC信息准则是AIC准则的替代方法。

通过对辽宁电力景气先行合成指数和辽宁全社会用电量建立VAR模型，对其进行滞后期检验，结果如图3所示。

Figure 3. Lag period checklist

图3. 滞后期检验表

结合AIC、SC和HQ信息准则，可以确定VAR模型的最佳滞后期为1期，即VAR(1)。

4.2. 单位根检验

数据具有平稳性是构建VAR模型的基础，而单位根检验则是检验时间序列是否平稳的最常用方法之一，因此，本文运用ADF检验(Augmented Dickey-Fuller Test)法对辽宁省全社会用电量及其电力景气先行指数时间序列进行平稳性检验。

ADF检验法的数学表达公式如下所示：

$\Delta y_t=\gamma y_{t-1}+{\displaystyle {\sum }_{i=1}^p{\beta }_i\Delta y_{t-1}}+{\mu }_i$ , $$ (5-8)

$\Delta y_t=\gamma y_{t-1}+\alpha +{\displaystyle {\sum }_{i=1}^p{\beta }_i\Delta y_{t-1}}+{\mu }_i$ , $t=1,2,\cdots ,T$ (5-9)

$\Delta y_t=\gamma y_{t-1}+\alpha +\tilde{\alpha }+{\displaystyle {\sum }_{i=1}^p{\beta }_i\Delta y_{t-1}}+{\mu }_i$ , $t=1,2,\cdots ,T$ (5-10)

其检验假设如下：

$\{\begin{array}{l}H0:\gamma =0\\ H1:\gamma <0\end{array}$ (5-11)

即原假设是时间序列存在单位根，而备选假设是时间序列不存在单位根 [5] 。

对VAR(1)模型进行ADF检验，结果如图4、图5所示。

Figure 4. ADF test form for electricity consumption in Liaoning

图4. 辽宁全社会用电量ADF检验表

Figure 5. Liaoning electric power boom synthetic index ADF test form

图5. 辽宁电力景气先行合成指数ADF检验表

可见，两个变量的时间序列在5%的显著水平下均为平稳的时间序列，即VAR(1)模型具有稳定性。

4.3. 格兰杰因果检验

在建立了VAR模型之后，要对其进行识别和检验，以判断其是否符合VAR模型最初的假定和经济意义。这其中最常用到的就是格兰杰(Granger)因果检验。

判断格兰杰原因的直接方法是利用F-检验方法进行检验。检验的原假设和备择假设分别为：

H0：；H1：至少存在一个q使得 $A_{12}^{\left(q\right)}\ne 0$ 。

其统计量为：

(5-13)

检验统计量服从精确的F分布。如果 $S_1$ 大于F的临界值，则拒绝原假设，即现在的y能够被先前的x解释，加入x的滞后值使解释程度提高，先前的x (x的滞后项)在y的预测中有帮助。若 $S_1$ 小于F的临界值，则不能拒绝原假设：x不能格兰杰引起y，也就是说先前的x对于现在的y没有显著的解释能力。

VAR回归模型存在着一个渐近等价检验，可由下式给出：

$S_2=\frac{T\left(RS{S}_O-RS{S}_1\right)}{RS{S}_1}~X^2\left(p\right)$ (5-14)

$S_2$ 服从自由度为p的 $X^2$ 分布。如果 $S_2$ 大于 $X^2$ 的临界值，则拒绝原假设；否则接受原假设。

在SPSS中的VAR模型检验就是用的格兰杰检验因果 $X^2$ 检验，而SPSS在Group中进行的格兰杰因果检验用的是标准的F检验。

对VAR(1)模型进行格兰杰因果检验，检验结果如图6所示。

Figure 6. Granger causality test

图6. 格兰杰因果检验表

格兰杰因果检验显示，辽宁电力景气先行合成指数是辽宁全社会用电量的格兰杰原因，全社会用电量不是电力景气先行指数的格兰杰原因。

4.4. 脉冲响应函数分析

由于在实际应用中，VAR模型是一种非理论性的模型。根据VAR模型的结构模型可以看出，对第i个变量的冲击会影响到第i个变量，同时也会影响到结果模型中的动态滞后结构中的其他内生变量。因此在分析VAR模型时，不仅分析一个变量的变化对另一个变量的影响如何，而且要分析当VAR模型受到某种冲击时对系统的动态影响 [6] 。分析这种动态影响的方法便是脉冲响应函数方法。

脉冲响应函数的表达式是VAR模型通过友矩阵变换得到的，其转换过程如下所示：

$Y_{t+s}=U_{t+s}+A_1{U}_{t+s-1}+A_1^2{U}_{t+s-2}+\cdots +A_1^s{U}_t+\cdots$ (5-15)

$Y_{t+s}=U_{t+s}+{\Psi }_1{U}_{t+s-1}+{\Psi }_2{U}_{t+s-2}+\cdots +{\Psi }_s{U}_t+\cdots$ (5-16)

其中， ${\Psi }_1=A_1$ ， ${\Psi }_2=A_1^2$ ， ${\Psi }_s=A_1^s$

所以，

${\Psi }_s=\frac{\partial Y_{t+s}}{\partial U_t}$ (5-17)

式子(5-17)即为脉冲响应函数(Impulse-Response Function)。

对VAR(1)模型进行脉冲响应检验，结果如图7所示。

用电量对其自身一个标准差扰动存在也存在反应，尤其是前两期反应较大，两期之后影响逐渐降低。

从辽宁全社会用电量对辽宁电力景气先行合成指数的响应角度看，前三期用电量对先行指数一个标准差的扰动存在正向响应，而后降落，但响应始终保持正值并趋于稳定，这说明两者之间存在长期关系。

从先行指数对全社会用电量的响应角度看，先行指数对用电量一个标准差的扰动存在正负交替的影响，前一期影响较大且为正值，第二期为负值，而后转正，第五期之后逐步收敛，且波动始终较小，说明先行指数受用电量的影响较小，而且持续时间较短。

Figure 7. Impulse response check chart

图7. 脉冲响应检验图

先行指数对其自身一个标准差的扰动呈现强烈的负向响应，前五期影响较大，此后逐步收敛，说明先行指数和其滞后值存在较大的关联。

4.5. 方差分解分析

与脉冲响应函数不同的是，方差分解时将内生变量中的一些变化进行分解，分解成为向量自回归模型的分量冲击。方差分解时将每个变量预测误差的方差分解为与各个内生变量相关联的组成部分 [7] 。

其表达式由如下的转换过程而来：

则第i个变量 $y_{it}$ 可以写成：

$y={\displaystyle {\sum }_{j=1}^p\left({\Psi }_{0ij}{\mu }_{jt}+{\Psi }_{1ij}{\mu }_{jt-1}+{\Psi }_{2ij}{\mu }_{jt-2}+{\Psi }_{3ij}{\mu }_{jt-3}+\cdots \right)}$ (5-18)

其方差为：

$E\left[{\left({\Psi }_{0ij}{\mu }_{jt}+{\Psi }_{1ij}{\mu }_{jt-1}+{\Psi }_{2ij}{\mu }_{jt-2}+{\Psi }_{3ij}{\mu }_{jt-3}+\cdots \right)}^2\right]={\displaystyle {\sum }_{q=0}^{\infty }{\left({\Psi }_{qij}\right)}^2{\sigma }_{ij}^2}$ (5-19)

定义：

$RV{C}_{j\to i}\left(\infty \right)=\frac{{\displaystyle {\sum }_{q=0}^{\infty }{\left({\Psi }_{qij}\right)}^2{\sigma }_{ij}^2}}{{\displaystyle {\sum }_{j=1}^k\left\{{{\displaystyle \sum }}_{q=0}^{\infty }{\left({\Psi }_{qij}\right)}^2{\sigma }_{ij}^2\right\}}}$ (5-20)

其中，RVC (Relative Variance Contribution)是相对方差贡献率。若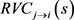小，表示第j个变量对第i个变量的影响小，反之，则大。

对VAR(1)进行方差分解分析，得到结果如图8所示。

Figure 8. Variance decomposition table

图8. 方差分解表

对辽宁电力景气先行合成指数和辽宁全社会用电量进行方差分解，从分解结果可以看出，辽宁全社会用电量的预测标准误差较大，并随着期数的增加不断扩大，先行指数对用电量的影响在第六期之后基本保持稳定，同时，辽宁全社会用电量受到自身的影响较大。先行指数预测标准误差较小，并在第四期之后逐步稳定，同时随着期数的增加，对自身的影响有所降低，但仍然是主要影响。

5. 结论与建议

通过相关性检验结果可以看出，辽宁全社会用电量及其电力景气先行合成指数之间存在稳定关系，且用电量受到先行指数的影响较大，而先行指数受到用电量的影响却有限。

因此，辽宁电力景气指数与辽宁电力总体需求密切相关，尤其是电力景气先行指数体现对辽宁省未来的电力需求总体情况的预测功能。而又由于先行指数中包含了辽宁省GDP、辽宁居民人均可支配收入等经济指标，因此可表明辽宁宏观经济因素会对其电力行业的生产供应，特别是对辽宁总体用电量产生影响。

同时，我国正处于改革的“攻坚区”和“深水区”，要求经济改革以调整结构为主攻方向。辽宁省作为我国最重要的重工业城市之一，以装备制造业、冶金、石化、农产品四大产业为支柱产业，必不可免会受到产业结构调整等宏观因素的影响，从而使其经济发展受到影响。而经济发展又与用电需求密不可分，当地区经济发展平稳或加速时，其工业生产也将扩张，从而拉动用电需求增加，使电力市场处于景气状态 [8] ；当地区经济增长放缓或低迷疲软时，社会对电力的需求量也会大幅下降，使电力市场也处于不景气的状态。因此，在我国经济及产业结构转型的大背景下，辽宁省未来电力需求的总体趋势将会受到宏观经济因素的影响，产生与先行经济指标相关的异常波动。

对此，辽宁省应该加强完善电力景气指数的预警监控机制，提高电力景气指数，尤其是电力景气先行指数对电力需求预测的准确性，实现从经济看电力的功能，做好电力需求侧管理，保障辽宁省的平稳健康发展。

参考文献