基于SURF算法的桥梁裂纹图像拼接技术

A Robust Approach for Bridge Crack Image Mosaic Based on SURF Algorithm

摘要: 针对现阶段桥梁健康检测中存在着多样化的裂纹问题，摄像机在确保清晰度的情况下很难获取一张高分辨率高精度的裂纹图像。本文在此问题上提出了基于SURF特征点的图像拼接技术研究在桥梁裂纹上的应用，对采集到的裂纹图像进行预处理，其中主要用了灰度处理突出特征点以及滤波方法去噪，利用SURF算法对裂纹图像进行特征点提取，通过欧氏距离的相似量方法进行特征点匹配，再采用RANSAC (Random Sample Consensus随机抽样一致性)算法剔除错误的匹配点对获得精确匹配，最后使用加权平均法融合图像实现图像拼接。本实验在光照、尺度变换、模糊等不同条件下，对SURF算法、ORB (Oriented Fast and Rotated BRIEF)算法和SIFT (Scale-invariant Feature Transform尺度不变特征变换)算法进行比较，研究结果表明，基于SURF算法裂纹图像拼接在不同环境下匹配精度更高，实用性和鲁棒性更强。因此，该算法在桥梁裂纹图像拼接具有较强的应用价值。

Abstract: Diversified crack difficulties occurred to the detection about bridge health at the present stage. Meanwhile, it is hard to obtain the high resolution and precision crack images accompanied with the insurance of the camera sharpness. Therefore, the image mosaic technology was applied to analysis of the bridge cracks based on the SURF (Speeded up Robust Features) algorithm. First of all, the captured crack images are mainly pretreated through gray processing to highlight the feature points and denoised by the way of filtering. Secondly, the feature points of the crack images are extracted by the SURF and matched through the similar quantity method of Euclidean distance. Thirdly, the RANSAC (Random Sample Consensus) algorithm is employed to eliminate the wrong match points and get an exact match. Finally, the weighted average method is used to fuse for the purpose of image mosaic. The SURF, ORB (Oriented Fast and Rotated BRIEF) and SIFT (Scale-invariant Feature Transform scale invariant feature transform) were compared by changing the environment factors like lighting, scale conversion, blurring in the experiment. The research results show that the image mosaic based on the SURF performs higher matching precision, more real-time and robustness in different environments. Therefore, it performs a strong application value in bridge crack image mosaic.

1. 引言

伴随着我国基础设施建设的日益发展，在交通建设中更是突飞猛进，不管是在基础道路还是高速公路或者铁路，其中桥梁都扮演着必不可少的角色。然而随着时间的增长，桥梁必然会出现损伤问题，在很多桥梁损害里面，裂缝其实是很难观察检验出来的一类损坏形态，也是桥梁健康检查的重点之一，现阶段对于桥梁裂纹的检测还是停留在人工操作，这种方式成本投入高，安全隐患大，效率更低。随着科技与计算机技术的迅速发展，关于数字图像方面的处理技术能够普遍使用在军事探测、航天航空以及工业机器人等相关领域，由此进入高速变革的阶段，其中图像拼接这种技术令许多我国境内和海外的探究成员有兴趣对其实施深层面的探究。然而随着人们对图像获得信息的需求越来越高，目前的一些硬件设施单一，还难以采集到高分辨率的宽视角图像，所以如何能在低成本等条件下采用数字图像处理技术获取高质量高分辨率的图像成为一个研究热点。

关于图像拼接这种技术而言，最为关键的就是对于图像实施配准操作 [1] ，其从广义上说能够划为2个类别：其一，以区块为基础的计算方法，该匹配算法较为传统，对待匹配图像的相似度要求较高，当中涵盖以空间为基础的像素配准方法等一系列相关部分；其二，以特征为基础的计算方法，通过使用图像内匹配的局部显著特点去确定图像间存在的几何转换关系。而这些年的探究焦点是以特征为基础的搭配方法，该方法有更好的计算速度和鲁棒性强，许多研究者在这方面都进行了广泛深入的研究。2004年，David G. Lowe [2] 提出了SIFT优化算法，具有旋转、亮度及尺度不变性。2006年，Herbert Bay [3] 等人提出了SURF算法，其在SIFT算法的基础上改进，具有快速性、尺度不变的特点。文献 [4] 指出一类以SURF为基础的图像拼接方法，关于这种计算方法，在特征点众多的声纳图像里面具备优良的精度，另外具备较佳的即时性。文献 [5] 将SURF算法应用到无人机遥感影像拼接，在运算速度和提取到的特征点数量均有较大进步。

为了获取一种快速实用性及高效的算法，来实现桥梁裂纹高质量的宽视角拼接图像，本文引用SURF算法在图像拼接中进行特征点的提取与匹配，通过RANSAC算法剔除错误的匹配点对，最后使用加权平均方法融合图像。在特征点的匹配上结合ORB算法与SIFT算法，在不同条件下得到的拼接效果来验证本文算法的实用性与鲁棒性。

2. 桥梁裂纹图像拼接技术

2.1. 裂纹图像预处理

在裂纹图像采集的过程中，会因为环境的多变复杂而出现的噪声干扰等存在，影响到后面拼接阶段图像特征匹配，为此图像预处理就变得必不可少。本文对拍摄到的裂纹图像主要做了灰度处理，将三通道的彩色图像变为单通道的灰度图像，在提取特征点过程中更能有效的生成描述子，同时也对图像进行了尺度变换，将原图像的尺寸做了缩放处理，有益于后续的匹配观察。

2.2. SURF算法

本文裂纹图像拼接采用SURF算法，进行特征点的提取与匹配，该算法是由Herbert Bay等人在SIFT算法基础上提出的一种快速高鲁棒性特征提取算法。其提取的特征具有旋转、尺度等不变性的特点，有很好的鲁棒性，适用于不同尺度、不同拍摄角度下图像处理，相比较其他算法更具有实时性和鲁棒性。

1) 积分图像

假设 $I\left(x,y\right)$ 为图像的某一像素点，则积分图像 $I_{\Sigma }\left(X\right)$ 的面积等于该点到原点的所有点的像素之和，即

$I_{\Sigma }\left(X\right)={\displaystyle \underset{i=0}{\overset{i\le x}{\sum }}{\displaystyle \underset{j=0}{\overset{j\le y}{\sum }}I\left(i,j\right)}}$ (1)

由上式可得，在任意一块矩形区域(如图1)的积分面积可以有式(1)得到：

$\Sigma =A-B-C+D$ (2)

Figure 1. Computes the integral image

图1. 计算积分图像

2) 特征点提取

在积分图像基础上，构建Hessian矩阵 $H\left(X,\sigma \right)$ 尺度为 $\sigma$ ，即

$H\left(X,\sigma \right)=\left[\begin{array}{cc}{L}_{xx}\left(X,\sigma \right)& L_{xy}\left(X,\sigma \right)\\ L_{xy}\left(X,\sigma \right)& L_{yy}\left(X,\sigma \right)\end{array}\right]$ (3)

其中 $L_{xx}\left(X,\sigma \right)$ 是图像 $I$ 与二阶高斯函数 $\frac{{\partial }^2}{\partial x^2}g\left(\sigma \right)$ 的卷积，同理可得 $L_{xy}\left(X,\sigma \right)$ 和 $L_{yy}\left(X,\sigma \right)$ 。为了提高运算效率，用盒子滤波器近似替代高斯滤波器，并且用 $D_{xx}$ ， $D_{xy}$ 和 $D_{yy}$ 来对应 $L_{xx}$ ， $L_{xy}$ 和 $L_{yy}$ 。而近似高斯计算Hessian矩阵行列式的估计公式为：

$\det \left(H_{\text{approx}}\right)=D_{xx}{D}_{xy}-{\left(\omega D_{xy}\right)}^2$ (4)

其中 $\omega$ 为权重，一般取0.9。根据以上行列式判断极值点，如果行列式的符号是负的，那么特征值具备差别的符号，认为此点并非部分极值点。假如行列式的符号是正的，那么它的2个特征值同是正的或是负的，认为该点为极值点。

SUFT这种计算方法组建尺度空间和SIFT计算方法有所不同，因为采用积分图像与盒子滤波，不必创建金字塔图像，选用盒子滤波样板持续增加尺寸这种办法，通过不同的盒子滤波来求得Hessian矩阵行列式的回应图形，将经过Hessian矩阵得到的多层数据利用非极大值抑制寻找到极值点，再将该点的DOH值与二维图像空间和尺度空间领域内的26个点进行比较，得到初步的关键点，之后剔除一些错误关键点，筛选出相对平稳的特征点。

3) 特征点描述

关于SUFT算法而言，在它的特征点描述中，首先我们需要确认特征点的主方向，确保其在转动过程中能够保持不变，在6 s (s代表特征点的尺度)作为半径长的圆形区块中，归纳60度的扇形区块中全部点在水平向、垂直向的Harr小波特征的总和，以步长为0.2弧度一定方向旋转，对窗口中Harr小波的回应值实施累加操作，最后将其最大值对照的方向确定成主方向。

其次我们要生成特征描述子，先要确定边长为20 s的正方形区域，再划分为 $4\times 4$ 的边长为5s小区域，每个小区域用2 s的Haar小波模板响应运算，然后对响应值统计 ${\displaystyle \sum dx}$ ， ${\displaystyle \sum \left|dx\right|}$ ， ${\displaystyle \sum dy}$ ， ${\displaystyle \sum \left|dy\right|}$ ，形成 $4\times 4\times 4=64$ 维的特征向量。

4) 特征点匹配

通过对距离集合进行比较运算得到最小欧式距离和次最小欧氏距离，设定一个阈值，当最小欧氏距离和次最小欧氏距离的比值小于该阈值时，则认为该特征点对应最小欧式距离的特征点是匹配的，否则没有与特征点相匹配。

2.3. 图像融合

在待拼接的图像进行预处理、特征提取与匹配、求出变换矩阵之后，便是要对两幅拼接的图像进行融合，其目的就是将不同的图像拼接在一起成为一幅完整的图像。本文主要利用的是加权平均法，其具有简单易实现、运算速度快的优点。

2.4. 桥梁裂纹图像拼接流程

本文的图像拼接实验是应用在桥梁裂纹上，其实验流程是先采集到裂纹图像进行预处理，包括用灰度处理突出特征点以及滤波方法去噪，然后同SURF算法进行特征点的提取，通过欧氏距离的相似量方法进行特征点匹配，利用RANSAN算法剔除误匹配，最后计算单应性矩阵用加权平均方法进行图像融合，实现裂纹图像拼接，如图2所示。

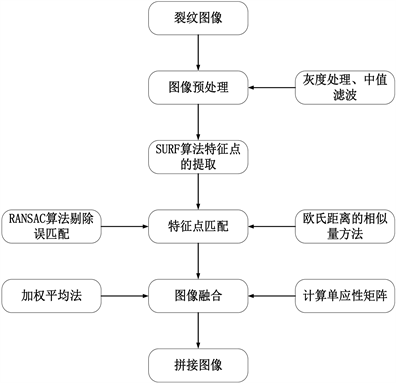
Figure 2. Crack image mosaic process framework

图2. 裂纹图像拼接流程框架

3. 实验数据比较与分析

本文实验采用的是CCD工业相机拍摄裂纹素材，具有500万像素足以获取需要的数据。实验的程序设计是在Visual Studio 2010进行，配置环境如表1所示。

Table 1. Experimental environment

表1. 实验环境

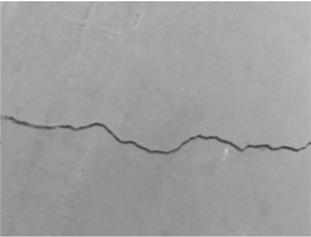
为了验证本文SURF算法在特征点的提取与匹配上的鲁棒性和实用性，实验分别在光照，噪声，尺度变换等条件下，对SURF算法、SIFT算法与ORB算法进行比较分析。图3为采集到的几张裂纹图像，图4为SURF算法进行图像匹配的效果图，图5为图像拼接后的效果图。

从表2中观察可以看到，执行速度上ORB算法最具有优势，SURF算法处理的时间只慢了0.5 s，一般表格的数据都是量化计数，本文实验观察中，会发现到大量的特征点分布杂乱无章，匹配精度和准确性上都受到了影响，表格中在成功匹配对数上SURF算法明显优越于SIFT和ORB算法，在拼接效果表现得也很好。对比看来SURF算法实用性上有更大的价值。

3.1. 尺度条件下的鲁棒性比较

图像在不同尺度下得到的特征点意义是不同的，尺度较大的图像提取到的特征点在小尺度下的图像中表现得可能不明显，不同尺度下的图像也会出现新的特征点。

Figure 3. Crack image

图3. 裂纹图像

Figure 4. SURF matching effect

图4. SURF匹配效果图

Figure 5. Mosaic effect chart

图5. 拼接效果图

Table 2. Comparison of the first set of three algorithm stitching data

表2. 第一组三种算法拼接数据对比

本实验方案取图1(b)为原图像，对其改变尺度大小，分别为缩小尺寸80%、60%、40%、20%，对应图6中横坐标1，2，3，4。尺度变换后的图像和原图像进行特征点匹配，逐一比较得到匹配对数，然后观察其变化幅度。

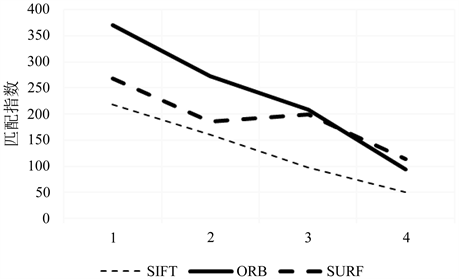
Figure 6. Matched logarithmic polygraph of each algorithm under scale transformation

图6. 尺度变换下各算法的匹配对数折线图

从折线图6中可以观察到SURF算法变化幅度最小,在尺度变换较大时匹配对数变化较小，匹配的对数较多，更趋于稳定。在尺度变换中SURF算法表现出更高的鲁棒性。

3.2. 光照条件下鲁棒性比较

在不同光照下，图像中的一些关键特征会由于阴影影响被弱化，而有些特征会更加突出，使得图像中的特征或者特征点并非处于相同的灰度尺度下。

本实验方案对一张图像逐渐增加亮度，见图7，逐一与原图像进行匹配，观察其正确匹配对数的变化幅度，对各算法进行比较分析。结果见图8。

Figure 7. Crack image at different brightness

图7. 不同亮度下的裂纹图像

Figure 8. Matching logarithmic polygraph of each algorithm under illumination

图8. 光照条件下各算法的匹配对数折线图

从图8中可以观察到，SURF算法在不同亮度下正确的匹配对数最多，变化的幅度的较小，相比较SIFT算法和ORB算法表现得更加稳定。

3.3. 模糊条件下鲁棒性比较

图像进行模糊变换后，其分辨率就会降低，随着分辨率的下降，其特征的识别精确度就会下降。

本实验方案对原图像用高斯噪声进行模糊处理，与原图像进行匹配，如图9所示，实验得到以下结果见表3。

(a) (b)

Figure 9. Crack original image and blurred image

图9. 裂纹原图像和模糊处理后的图像

Table 3. Data comparisons of algorithms under fuzzy conditions

表3. 模糊条件下各算法的数据对比

从表3中可以观察到，各算法执行时间从大到小依次为SIFT、SURF、ORB，SURF算法成功匹配对数明显优于ORB和SIFT算法，拼接质量更佳，通过比较模糊条件下简单比较，SURF算法鲁棒性表现得更好。

图10为三张互有重叠的裂纹图像用SURF算法拼接后的效果图，可以观察到基本将裂纹拼接为一幅完整的宽视角高分辨率的图像。

Figure 10. SURF mosaic effect diagram

图10. SURF拼接效果图

4. 结论

近年来，全景图像拼接的应用越来越广泛，例如虚拟现实、视频监控以及街景地图等。那么随着这一技术的广泛应用，当前算法中存在的拼接效率低、计算量大以及拼接存在误差等问题也成为限制其应用的重要问题，阻碍了相关应用的发展，因此对图像拼接技术质量和效率的提升成为了图像领域研究的热点问题。本课题主要研究的是如何在保证图像拼接质量的前提下，提高图像拼接的计算速度。文章通过分析传统基于SURF特征匹配的图像拼接方法的缺陷，提出改进方法来加快图像拼接的速度，通过理论部分的可行性研究分析以及仿真实验，实验结果证明了改进方法的可行性，但是本论文仍然存在一些可以继续研究和改进的地方。

1) 本文提出的图像局部特征自适应的快速SURF图像拼接方法中获得的复杂度阈值是通过方差的计算得到的，接下来在复杂度阈值获取的精度和速度上还有改进空间。

2) 对于待拼接图像间变换关系更为复杂的拼接实验有待进一步研究。本文中测试的待拼接图像仿射变换关系不是特别复杂，若图像间仿射变换较大，测试得到的重叠区域可能不太准确，而且拼接结果的清晰度也会有所下降。所以下一步的工作可以针对仿射变换较大的图像序列进行拼接优化。