六方AlN(0001)面极化性质的最大局域化Wannier函数方法研究

Polarization Properties of Hexagonal AlN(0001) Surface from Maximally Localized Wannier Functions

摘要: 采用最大局域化Wannier函数方法，研究了六方AlN(0001)面的电子结构及其极化性质。发现由于表面电荷重新分布及离子移动，表面的极化显著大于体相结构中的极化值。逐层分析表面结构极化性质的变化，发现极化迅速衰减，经过大约10 Å厚度，达到体相结构中的极化值。研究结果对于理解基于AlN的表面吸附以及薄膜科技应用有着指导意义。

Abstract: Using the maximally localized Wannier functions, polarization properties of hexagonal AlN(0001) surface was investigated. It was found that polarization of the surface layer is dramatically larger than that of the bulk due to the charge rearrangement and ions relaxation. Analyzing the polarization properties layer by layer, we found that the polarization value declines rapidly and approaches to the bulk value after about a depth of 10 Å. These findings are of guidance for un-derstanding the surface adsorption and thin film technology based on AlN.

1. 引言

六方纤锌矿氮化铝(AlN)是典型的第三代半导体材料，具有禁带宽度大(6.2 eV)、电子迁移率高、导热率高、压电系数大等一系列优点。这使AlN在深紫外发光及光电探测器件 [1] [2] 、高频大功率电子器件、压力传感器 [3] [4] 等方面有广泛的潜在应用。如2006年Taniyasu等 [5] 报道在实验室做出了直接基于AlN的辐射波长为210 nm的LED，2010年又报道做出了基于AlN非极性面的LED [6] 。此外，AlN和GaN、InN可以组成三元或四元合金，发光频谱更是覆盖了从红外到紫外的整个区域，是目前重要的半导体光电材料。

表面性质是半导体材料物理和化学性质的重要组成部分，近年来AlN表面性质研究受到越来越多的关注 [7] [8] [9] [10] [11] 。在AlN各种纳米结构及薄膜外延生长中，表面体积比很大，此时表面就极大影响着材料的各项性能。其中一个主要因素是由于表面原子存在化学键的断裂，破坏了表面的对称结构，产生了极化效应，进而影响着结构的各项性能。如在AlN纳米线的压电性质研究中，发现由于纳米线表面极化的影响，纳米线的压电常数相比体相结构有了显著提高 [12] 。因此AlN表面极化性质的研究在实际应用和基础研究方面都有着重要的意义。 $\left(000\bar{1}\right)$ 面是AlN最常见的一个密排面，一般的晶体生长都在这个面上进行。本文根据现代极化理论，利用最大局域化Wannier函数方法研究了AlN $\left(000\bar{1}\right)$ 表面的电子结构及极化性质，与AlN体相结构中的极化进行了比较，并逐层分析了表面结构中极化的变化。

2. 计算模型及方法

2.1. 计算理论

晶体的电子结构一般使用倒空间的布洛赫波函数 ${\psi }_{nk}\left(r\right)$ 进行表征。自1937年Wannier函数提出后，也可以用它代替布洛赫波函数对晶体电子结构进行描述。二者的关系为 [13] ，

$|\text{R}n\rangle =\frac{V}{{\left(2\text{π}\right)}^3}{\displaystyle {\int }_{BZ}{\displaystyle \underset{m=1}{\overset{N}{\sum }}{U}_{mn}^{\left(k\right)}|{\psi }_{mk}\rangle {\text{e}}^{-ik\cdot R}\text{d}k}}$ (1)

(1)式中V为单胞的体积，R为晶格矢量，n为能带参数，N为电子占据的能带数， $U_{mn}^{\left(k\right)}$ 为幺正矩阵。Wannier函数其实与布洛赫波函数互相满足傅里叶变化，由于布洛赫波函数具有 ${\psi }_{n\left(K+G\right)}\left(r\right)={\psi }_{nk}\left(r\right)$ ，导致Wannier函数不唯一。相比倒空间的非局域性的布洛赫函数，尽管实空间中的Wannier函数具有局域的特点，但是不唯一性长时间以来限制了它的应用。

1997年，Marzari与Vanderbilt提出了最大局域化Wannier函数(MLWF) [14] ，所谓最大局域化即引进了一个定义明确的局域标准，该标准引进了一个延展函数，可写为，

$\Omega ={\displaystyle \underset{n}{\sum }\left[\langle 0n\left|r^2\right|0n\rangle -{\langle 0n\left|r\right|0n\rangle }^2\right]}={\displaystyle \underset{n}{\sum }\left[{\langle r^2\rangle }_n-{\bar{r}}_n^2\right]}$ (2)

(2)式中 $|0n\rangle$ 表示原点处的第n个Wannier函数， ${\langle r^2\rangle }_n$ 及 ${\bar{r}}_n={\langle r\rangle }_n$ 分别是 $\langle 0n\left|r^2\right|0n\rangle$ 和 $\langle 0n\left|r\right|0n\rangle$ 的期望值， ${\bar{r}}_n$ 又称为Wannier中心。 $\Omega$ 其实是对原点处的Wannier函数在空间中的扩展的一个测量。通过对 $\Omega$ 求梯度，利用最速下降法或者共轭梯度法，当 $\Omega$ 相邻两步迭代的差值小于设定的一个参考值时(一般小于10⁻⁶ Ų)，将求得的 $U_{mn}^{\left(k\right)}$ 代入(1)式可求得MLWF。与第一性原理计算相比，最大局域化Wannier函数可以认为是一种后处理方法，根据第一性原理计算得到基态电子波函数，再利用上述计算可得到最大局域化Wannier函数进行后续的分析。

在计算出MLWF后，电荷可以形象地认为局域在Wannier函数空间分布的几何中心上，该几何点即为Wannier中心，位置在 ${\bar{r}}_n={\langle r\rangle }_n$ 。因此就可以将Wannier中心看作点电荷，从而整个晶体就可以分为带正电的离子与带负电的Wannier中心，进而分析体系的极化。

2.2. 计算模型

以纤锌矿AlN单胞(Vasp软件结构优化后得到的晶格参数为a = 3.1284 Å，c = 5.0146 Å，u = 0.3816)为基础，构建了(1 × 1)的 $\left(000\bar{1}\right)$ 面模型。为了消除模型下表面Al悬挂键的影响，用1.25个电子的赝氢原子对下表面进行了饱和。为了测试表面效应影响到模型多少层，构建了的含有16个双原子层的模型，真空层的厚度设为15 Å，结构优化时不固定任何原子层，发现16个双原子层的模型已经达到要求。如图1所示，结构优化后，从第四个双原子层开始，[0001]方向键长已结与体相结构中的键长相等，因此后续计算选用该模型。

采用第一性原理计算软件Vasp进行了表面结构优化及后续的静态及非静态自洽计算 [15] ，交换关联势选择广义梯度近似(GGA)下的PBE泛函进行处理，利用PAW赝势描述电子与离子实之间的势场，平面波截断能设为450 eV，K点网格设为9 × 6 × 1，结构中每个原子位置达到收敛的标准为原子上的受力小于0.01 eV/Å。最大局域化Wannier函数的计算使用了Wannier90 软件包 [16] 。

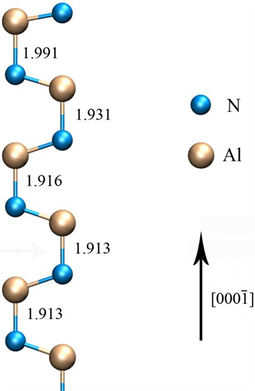
Figure 1. Side view of the relaxed AlN $\left(000\bar{1}\right)$ surface

图1. 结构优化后的AlN $\left(000\bar{1}\right)$ 面侧视图

3. 计算结果及讨论

3.1. 表面优化及电子结构

图1显示了优化后AlN $\left(000\bar{1}\right)$ 面结构及键长变化。发现在最外层，N原子向表面内侧移动了0.24 Å，Al原子轻微向外侧移动0.031 Å，原子层间距从第四层开始已经接近体相结构中的结果。根据最大局域化Wannier函数方法理论，表面电子结构的变化可由表面Wannier中心的分布直观表征。为了计算表面结构的最大局域化Wannier函数，首先计算了AlN $\left(000\bar{1}\right)$ 面的能带结构，如图2(a)黑线所示，由于表面悬挂键的存在，在靠近价带顶位置引入了一条能带，并被费米能级穿越。我们根据能带结构计算了整个价带对应的Wannier函数，为了判断得到的最大局域化Wannier函数的质量，利用Wannier函数进行插值计算得到了该组Wannier函数对应的能带，如图2(a)红线所示，可以看到其与利用第一性原理计算得到的能带结构符合得很好，说明求解最大局域化Wannier函数过程符合要求。

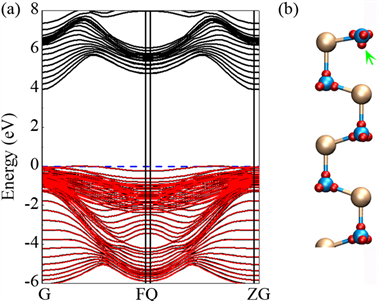
Figure 2. (a) DFT (black line) and Wannier interpolated (red line) band structure of AlN $\left(000\bar{1}\right)$ surface, the fermi level is set at 0 zero. (b) Wannier centers (red balls) distribution of AlN $\left(000\bar{1}\right)$ surface

图2. (a) 第一性原理计算得到的能带(黑线)与Wannier函数插值得到的能带(红线)，费米能级设为0 eV(蓝色虚线)。(b) 表面Wannier中心(红色小球)分布

图2(b)显示了AlN $\left(000\bar{1}\right)$ 面Wannier中心的分布，首先可以看到结构中Wannier中心非常靠近N原子，说明电荷向N原子发生了转移，也清楚地表明N-Al键具有很强的离子性。其次在最外层上，四个Wannier中心的分布偏离了N-Al键的方向，不同于内层结构中的Wannier中心分布，表明由于最外层上悬挂键的存在，使得电荷发生了明显的重新分布。从绿色箭头所指的Wannier中心来看，一方面表明Al悬挂键上的电子转移到N原子，另一方面由于N原子较强的吸引力，最外层N悬挂键上的电子也转移到N原子的另一侧，由于电荷之间的斥力，使得Wannier中心偏离了N-Al键方向。

3.2. 表面极化性质

表面离子移动和电荷的重新分布，影响着表面极化性质。根据现代极化理论 [13] ，在最大局域化Wannier函数表象中，可以将图2(b)所示的表面结构看成由+5 N、+3 Al离子以及−2 Wannier中心构成的

Figure 3. Dipole moment variation as the layer distance, bulk value is depicted by the blue dash line

图3. 偶极矩随层间距变化关系，蓝色虚线为体相结构中极化值

点电荷群，表面结构中最小重复单元是N-Al对，因此利用经典的电极化理论计算出表面结构中每个原子层包含的N-Al对的平均偶极矩，就可以逐层分析结构中极化性质的变化。根据这种方法计算出的纤锌矿AlN体相结构中的N-Al对的平均偶极矩为0.566 D (单位为德拜)，对应于体相结构中自发极化为0.090 C/m²，与其他文献利用Berry phase方法得到的结果一致 [17] 。

图3逐层给出了AlN $\left(000\bar{1}\right)$ 面结构中极化性质的变化，可以看到最外层极化性质变化最大，为−2.996 D，显著大于体相结构中的极化性质，负号表示极化方向发生了逆转，这主要是由于表面N原子发生了明显的向内侧移动造成的。从第二层开始，极化值迅速衰减，在第五层时已经趋于体相结构中的极化，显示出表面效应对整个结构极化性质的影响限于表面5个原子层内(约10 Å的厚度)，因而存在微观而不是宏观的影响。但由于表面极化数值大，因此表面极化对表面吸附作用将产生重要影响。如Kolpak等利用密度泛函理论研究了以铁电PbTiO₃为基底的超薄Pt薄膜上的CO分子吸附，发现PbTiO₃基底的极化效应可以显著改变分子化学吸附能 [18] ，Zhao等利用程序升温脱附法(TPD)研究了极化效应对BaTiO₃吸附乙醇的影响，发现乙醇的吸附依赖于BaTiO₃的极化方向 [19] 。近年来，极化效应对表面化学性质及光催化性质的影响已经有了一系列实验报道 [20] 。

AlN晶体的结构导致其在III族氮化物半导体中具有最大的自发极化，其自发极化值仅比经典的钙钛矿型铁电体小3~5倍，更是远大于一般其他III-V和II-VI族化合物的自发极化 [21] ，是目前发现的纤锌矿结构晶体中自发极化最大的，AlN表面极化性质相比体相结构又有了显著增大，因此在AlN薄膜科技及其表面性质应用中，表面极化性质的变化也要作为一个主要因素进行考虑。

4. 总结

利用最大局域化Wannier函数方法，逐层分析了AlN $\left(000\bar{1}\right)$ 面结构中极化性质的变化，发现由于表面离子移动以及电荷重新分布，导致最外层极化值远大于体相结构中的极化，由表层向内，极化值迅速减小，经过大约10 Å，极化值接近体相结构中的极化值，说明表面极化效应是一个微观现象。

基金项目

本研究受到陕西省教育厅专项科研计划项目(编号：16JK2099)资助。