落石冲击力理论与数值模拟研究

Research on the Theory and Numerical Simulation of Rockfall Impact Force

摘要: 落石冲击力是棚洞结构设计时需要考虑的主要荷载之一。运用LS-DYNA数值模拟二十六面体落石冲击混凝土棚洞结构，并将数值结果与现有的落石冲击力理论计算方法的结果对比分析，结果表明：国内推荐使用的落石冲击力计算方法严重偏小，日本公式计算结果最大。各个理论计算方法的结果相差巨大，为保证棚洞结构的偏安全设计，建议使用日本公式计算落石冲击力。

Abstract: The impact force of falling rock is one of the main loads to be considered in the design of tunnel structure. ANSYS/LS-DYNA numerical simulation was used to simulate the structure of concrete shed and cave impacted by falling rock. The numerical results were compared with the results of the existing theoretical calculation methods of rockfall impact. The results show that the recom-mended method for calculating rockfall impact force in China is seriously small, and the Japanese formula gives the largest result. The results of various theoretical calculation methods vary greatly. In order to ensure the partial safety design of the shed and cave structure, it is suggested to use the Japanese method to calculate the rockfall impact force.

1. 引言

落石是山区常见的灾害，对其危害范围内的公路、铁路等构筑物和人类活动构成了严重的威胁。棚洞作为一种有效的被动防护措施，目前已广泛地建造于落石易发处，来保护山区公路和铁路，防止交通堵塞。落石冲击力是棚洞结构设计时需要考虑的主要荷载之一。国内外学者对冲击力的研究主要基于四个理论：动量定理、弹性力学、接触力学和塑性变形 [1] 。

为了保护棚洞的下部结构，设计人员通常在棚洞上部铺置一定厚度的砂土垫层来缓冲落石对棚洞结构的冲击。落石冲击土层时包含了土层的弹性、塑性变形，也伴随着粘性、硬化和摩擦能量耗散等行为，导致冲击过程更加复杂。因此学者们对于落石冲击的研究大多基于冲击实验结果推导半经验半理论公式：日本道路公团 [2] 和Labiouse瑞士公式 [3] 基于Hertz弹性接触理论和室内落石冲击试验数据结果，提出计算落石冲击力的半经验半理论公式；Pichler [4] 等结合室外实验，根据落石冲击深度、落石高度计算其冲击力及冲击时间；杨其新、关宝树教授 [5] 通过对室内落锤实验数据拟合，建立落石冲击力计算方法。另外，国内的《公路路基设计规范》(JTJ13-95) [6] 和《铁路工程设计技术手册·隧道(修订版)》 [7] 也推荐了落石冲击力的近似算法。

然而实际工程中，山区落石的形状各异，冲击能量较大，当落石冲击砂石等缓冲层后，造成的压痕较深变形较大，Hertz弹性理论的小应变假设已经不能应用于伴随着塑性变形的落石冲击力的理论研究。各个理论计算方法通常采用球形落石的形式，而忽略了落石形状对冲击力的影响。从理论上、数值上和实验上，对落石形状对冲击力和结构响应的影响研究较少。徐胜 [8] 通过数值模拟表明：在同等条件下，落石形状的不同会导致冲击力大小也不同，其中正方形时，落石冲击力最大。Peng Yan, Jinhua Zhang [9] 等人通过数值模拟发现，与圆形落石相比，椭球体随着球度的增大，峰值冲击力和冲量增大。因此本文在考虑落石形状的情况下，通过数值模拟二十六面体落石冲击混凝土棚洞结构，来研究现今推荐使用的各个落石最大冲击力的计算方法是否依然适用。

2. 代表性的落石冲击力计算方法

2.1. 日本公式

Kawahara [2] 等基于Hertz弹性理论和落石冲击试验数据，给出最大冲击力公式为：

$F_{\max }=2.108{\left(mg\right)}^{2/3}{\lambda }^{2/5}{H}^{3/5}$ (1)

式中： $m$ 为落石质量(t)； $g$ 为重力加速度( $\text{m}\cdot {\text{s}}^{-2}$ )； $\lambda$ 为拉梅常数(kPa)，且 $\lambda =\frac{vE}{\left(1+v\right)\left(1-2v\right)}$ ， $v,E$ 分别为缓冲层的泊松比和弹性模量； $H$ 为落石下落高度。

2.2. 瑞士公式

Labiouse [3] 基于Hertz弹性理论和落石冲击试验数据，给出最大冲击力公式为：

$F_{\max }=1.765\times M_E^{2/5}\times R^{1/5}\times {\left(QH\right)}^{3/5}$ (2)

式中： $M_E$ 为缓冲层的弹性模量(kPa)； $R$ 为落石等效半径(m)， $R=\sqrt[3]{\frac{3m}{4\text{π}\gamma }}$ ， $m$ 为落石质量(kg)， $\gamma$ 为落石密度(kg/m³)；Q为落石重量(kN)；H为落石下落高度(m)。

2.3. 隧道手册公式

《铁路工程设计技术手册–隧道》 [7] 给出了冲击力近似计算方法：

$F=\frac{Q{v}_0}{gt}$ (3)

式中：Q为落石重量(kN)； $v_0$ 为落石冲击速度(m/s)； $g$ 为重力加速度( ${\text{m}/\text{s}}^2$ )；t为冲击持续时间， $t=\frac{2h}{c}$ ，其中 $c=\sqrt{\frac{1-v}{\left(1+v\right)\left(1-2v\right)}\times \frac{E}{\rho }}$ ， $v,E$ 分别为缓冲层的泊松比和弹性模量， $\rho$ 为回填土密度(kg/m³)。

2.4. 杨其新算法

杨其新教授 [5] 等通过室内试验数据，提出了一套经验公式：

$F=ma其中a=\frac{\sqrt{2gH}}{t},t=\frac{\left(0.097mg+2.21h+\frac{0.045}{H}+1.2\right)}{100}$ (4)

式中： $m$ 为落石质量(t)； $a$ 为冲击过程中的平均加速度( ${\text{m}/\text{s}}^2$ )， $g$ 为重力加速度( ${\text{m}/\text{s}}^2$ )；t为冲击持续时间(s)；H为落石下落高度(m)；h为缓冲层厚度(m)。

3. 二十六面体落石冲击棚洞结构数值模拟

为了探究落石对落石最大冲击力的影响，本文以G245线乌斯河至甘洛县城段公路改建工程棚洞为背景 [10] ，结合ANSYS/LS-DYNA截取其中6 m × 12 m进行数值模拟，重点研究在不同下落高度时，棚洞结构的动力响应和最大落石冲击力。通过与各个落石冲击力理论计算结果对比，以期为工程实际中棚洞结构设计时落石冲击荷载的选取提出建议。

3.1. 落石与棚洞材料参数

本文棚洞结构主要分为上下两个部分，上部为钢筋混凝土T型梁，下部为混凝土顶端梁，混凝土棚洞模型如图1所示。根据JTG/TD70-2010《公路隧道设计细则》 [11] 规定，当边坡有严重的危石、崩塌威胁时，棚洞顶板的回填土厚度不宜小于1.5 m，因此在棚洞顶板上铺设1.5 m砂土缓冲层。

由于实际工程中，落石的形状并非规则的球体，为了使冲击结果与实际工程更相近，因此落石采用一个切角的二十六面体混凝土重锤，如图2，质量为316 kg，尺寸如图2所示。

Figure 1. Structure model of shed

图1. 棚洞结构模型

Figure 2. Rockfall model Figure 2Rock fall size

图2. 落石模型图2落石尺寸

主要材料参数如表1。

Table 1. The material parameters

表1. 材料参数

3.2. 落石冲击棚洞结构的数值模型

本文运用ANSYS/LS-DYNA软件，建立与实际工程一致的模型，通过显示动力算法模拟落石冲击混凝土棚洞的全过程。

材料模型：针对钢筋混凝土冲击过程中破坏大变形问题，选择合适的混凝土本构关系至关重要。混凝土标号为C30，采用HJC材料模型，该模型因其简明合理的描述和计算程序的适应性，在混凝土强动载问题中获得了世界范围的广泛应用 [12] 。其材料参数见表2。

Table 2. Concrete material model of HJC

表2. HJC混凝土材料模型

对于纵向钢筋、板受力筋和箍筋用弹塑性模型下的各向同性硬化材料模型 MAT_PLASTIC_KINEMATIC来模拟，塑性硬化模量假设为钢筋弹性模量E_S的1%，屈服条件基于Von Mises准则。忽略砂体的破坏，使用MAT_CRUSHABLE_FOAM材料模型进行模拟，砂垫层应力应变关系采用Tam SyHO等人室内实验测得的以二阶抛物线关系表示 [13] ，其应力应变本构关系为 ${\sigma }_{sand}=50{\epsilon }_{sand}^2$ 。不考虑冲击过程中落石的分解、和土层飞溅的现象，将落石定义为刚性材料模型，并限制除竖直方向平动外的所有自由度。

接触设置：落石与砂土垫层采用面面普通接触，落石的刚度大设为目标面，垫层设为接触面。砂垫层与棚洞顶板之间采用面面自动接触，上部T型梁与下部顶端梁之间采用面面普通设置。荷载条件设置：落石垂直自由落体，对整个模型全部施加重力荷载，去加速度为9.8 ${\text{m}/\text{s}}^2$ 。边界及约束条件设置：顶端梁下部节点全部约束，并固定所有的自由度。

数值分析中的单元(落石、混凝土、泡沫、砂)均采用SOLID 164单元，T型梁各钢筋采用BEAM 161单元。以此建立的整体模型共有28,617个节点，8300个Beam单元，17,195个Solid单元，整个模型共有25,495个单元，如图3。

Figure 3. The element model

图3. 有限元模型

3.3. 数值模拟结果与理论计算结果对比分析

通过数值模拟给出二十面体落石在下落高度分别为1 m、2 m、3 m、4 m、5 m、6 m时，落石的最大冲击力。现将不同落石高度下各个公式冲击力计算结果与数值模拟结果作比较，如图4。

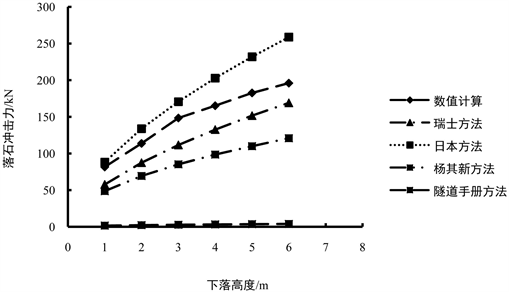
Figure 4. The results of various theoretical algorithms are compared with those of numerical simulation

图4. 各个计算结果与数值模拟结果对比

由图4可以看出，随着落石高度的增加，隧道手册方法的计算结果几乎没有增加外，各个算法的冲击力结算结果都在增加。可以明显看出针对同一种工况，不同的冲击力计算方法所得的结果却相差甚大。其中隧道手册方法计算结果最小，且随着高度的增加，冲击力却几乎没有变化。通过表3的误差分析可以看出，隧道手册误差几乎达到百分之百，对落石冲击力的估算严重不足。这是由于隧道手册方法是基于冲量定理，因而求得的冲击力是整个冲击过程中的平均值，但是落石冲击棚洞缓冲层是一个脉冲式的过程，冲击力变化极大，显然隧道手册方法求得的平均冲击力是远远小于最大冲击力的。杨其新方法是基于室内试验数据和牛顿第二定律，求得的加速度是平均加速度，因此冲击力也远小于最大冲击力，且室内试验冲击能量较小，而本文冲击能量较大，这也是造成其冲击力结果偏小的原因。日本和瑞士方法二者均为基于落石现场试验实测冲击力结果所建立，因此都与数值模拟结果过较为接近，两种方法计算结果的高低，前者取决于拉梅常数，后者取决于垫层变形模量参数的大小。瑞士公式中将落石简单的简化成球体，并未考虑落石形状对冲击力的影响，所求得的落石半径小于二十六面体真实半径，这也是瑞士公式冲击力小于数值模拟结果的原因。而日本方法是基于赫兹接触理论，其初始接触为点接触，且其弹性变形的小应变假设与实际不符，未考虑缓冲层的塑性变形，而本文模拟工程中，落石与缓冲层初始接触是平面接触，由于平面接触接触面较大，塑性变形吸收较大能量，致使日本方法得到的冲击力较大于数值模拟结果；且日本公式计算结果较大的依赖于拉梅常数的取值，一旦选取较小则远小于实际工程中的冲击力，因此往往选取偏大的拉梅常数，这也是日本方法结果大于数值模拟的一个原因。

Table 3. The results of various theoretical algorithms are compared with those of numerical simulation

表3. 各个理论算法结果与数值模拟结果对比

注： ${\zeta }_1=\left|F_1-F_5\right|/F_5;{\zeta }_2=\left|F_2-F_5\right|/F_5;{\zeta }_3=\left|F_3-F_5\right|/F_5;{\zeta }_4=\left|F_4-F_5\right|/F_5$ 。

由于没有完善的落石冲击力理论，中国实际工程中落石冲击力的选取都是参照隧道手册计算。而隧道手册方法计算所得冲击力严重偏小，造成实际工程中棚洞结构极易失效破坏，不仅极大的增大了后期维护成本，也对行驶在该路段的车辆安全具有较大威胁。

因此在没有最接近落石冲击棚洞结构的力学模型时，推荐使用日本公式计算落石冲击力，对棚洞进行偏安全设计。在今后的落石冲击力理论研究中，应该将落石冲击理论的研究中应考虑落石形状对冲击力的影响。

4. 结论

本文以G245线乌斯河至甘洛县城段公路改建工程棚洞为背景，结合数值模拟，对比研究当落石形状为二十六面体时，现今推荐使用的落石冲击力计算方法的结果的优劣，结果表明：

1) 由于日本公式的计算结果是最大的，因此在我国的工程实践中，对于棚洞结构设计时，出于偏安全的考虑，推荐使用日本公式计算落石的最大冲击力，并选取偏大的拉梅常数。

2) 现有落石冲击力计算方法都是基于实验结果的拟合公式，公式中的参数大多没有物理意义，因此导致各个公式计算结果相差千百倍，在今后的研究中，应该提出更为合理的力学模型，建立完善的冲击力理论体系。

3) 现有的落石冲击力计算方法都未考虑落石形状对冲击力的影响，在今后的冲击力理论计算方法研究中，应当考虑落石形状这一重要影响因素。

NOTES

^*通讯作者。