径向小孔节流静压轴承的静动特性分析

Analysis of Static and Dynamic Characteristics of Radial Hole Throttling Hydrostatic Bearing

摘要: 针对转速对静压气体轴承的影响不可忽略，提出了对径向小孔节流气体静压轴承的静动态性能分析。通过求解非定常雷诺方程，建立线性扰动理论和迭代过程。数值计算了轴承在不同转速，气膜厚度以及供气压力工况下的承载性，动刚度和动阻尼。结果表明，轴颈旋转对轴承静动态性能有重要影响，小孔节流静压径向轴承的垂向主刚度和主阻尼对扰动转速有很大的依赖性。

Abstract: The influence of rotation speed on aerostatic bearing can not be ignored. The static and dynamic performance analysis of radial hole aerostatic bearing is put forward. The linear perturbation theory and iterative process for solving the unsteady Reynolds equation are established. The bearing capacity, dynamic stiffness and dynamic damping of the bearing under different speeds, gas film thickness and gas supply pressure are numerically calculated. The results show that the journal rotation has an important influence on the static and dynamic performance of bearings. The vertical stiffness and main damping of the pinhole throttling hydrostatic bearing are very dependent on the disturbance speed.

1. 引言

气体轴承相比较传统轴承有着摩擦力小、高速、无污染的有点；是因为利用了空气作为润滑介质，所以相对传统的轴承转子系统，气体轴承有着替代的作用。但由于气体存在可压缩性，导致了气体轴承稳定性较差，刚度和承载性不高的缺点；由于具有良好润滑支撑性能，静压气体轴承被广泛应用于航空航天、火箭技术等先进技术领域 [1] [2] 。

Li [3] 提出了一种基于有限差分法(FDM)求解雷诺数方程的新迭代法，分析了高速气体轴承，同时通过改变设计参数来研究承载能力和刚度。Su [4] 分析了静压轴承的旋转效应，并且通过计算得到，承载力变化不是随着供气压力无限制增大。Chen [5] [6] 在文献中研究了由静压轴承支撑的刚性主轴的静态和动态特性，通过扰动法获得的刚性转子–气动系统的运动方程式的临界惯性力和临界旋转比的稳定性值，考虑了各种偏心度、转子速度和限制参数，并且分析了节流孔个数和位置对静压轴承的影响，同时得出了轴承的几何特征对气体轴承的刚度有显著影响。Wang [7] [8] 文献中研究了气膜支撑的柔性转子的分叉和非线性现象，采用连续过度关联法的有限差分法求解雷诺方程，得到了轴承运行轨迹、能量图、功率频谱和分岔图等动态特性，分析和揭示了复杂的动态行为，包括转子和轴颈中心的周期性和次谐波响应。同时文献分析了这种柔性系统中动态特性是如何随着转子质量和转速的变化而变化；这项研究的结果有助于进一步了解气体轴承转子系统的非线性动力学。张敏 [9] 研究了多孔材料在流场下的变形特性及其对轴承静态性能的影响。

针对径向气体轴承的刚度、阻尼、以及承载性的研究，本文创新性的利用扰动理论提出轴向扰动和径向扰动对气体轴承的影响，通过求解非定常雷诺方程，得到径向节流小孔静压轴承的静动态特性。

2. 数学模型

2.1. 润滑分析

为了得到径向节流小孔静压轴承的静动态特性，必须解非定常雷诺方程。需要对屋里模型进行假设：

1) 空气是等温和层流的。

2) 温度的变化被忽略，空气的粘度是恒定的。

3) 空气是理想气体之一。

得到径向小孔节流气体轴承的润滑方程：

$\begin{array}{l}\frac{\partial }{\partial x}\left(h^{3}p\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial z}\left(h^{3}p\frac{\partial p}{\partial z}\right)+12\eta \frac{p_a}{{\rho }_a}\rho \tilde{v}\\ =12\eta \frac{\partial \left(ph\right)}{\partial t}+6\eta V_{x1}\frac{\partial }{\partial x}\left(ph\right)+6\eta V_{z1}\frac{\partial }{\partial z}\left(ph\right)\end{array}$ (1)

h是空气膜厚度，可以表示为

$h=h_m\left(1+\epsilon \cos \theta \right)$ (2)

由于轴颈相对于轴承瓦的轴向速度为零，因此式(1)可以简化为

$\begin{array}{l}\frac{\partial }{\partial x}\left(h^{3}p\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial z}\left(h^{3}p\frac{\partial p}{\partial z}\right)+12\eta \frac{p_a}{{\rho }_a}\rho \tilde{v}\\ =12\eta \frac{\partial \left(ph\right)}{\partial t}+6\eta u\frac{\partial }{\partial x}\left(ph\right)\end{array}$ (3)

其润滑方程采用无量纲处理，无量纲参数变化如下：

$\bar{h}=h/h_m$ , $\bar{p}=p/p_r$ , $\bar{x}=x/l$ , $\bar{z}=z/l$ , $t=\tau /{\omega }_s$ , $\lambda ={\omega }_s/\omega$ , $\Lambda =\frac{6\eta \omega R^2}{p_a{h}_m^2}$

通过无量纲将公式(3)

$\begin{array}{l}\frac{\partial }{\partial \bar{x}}\left({\bar{h}}^3\bar{p}\frac{\partial \bar{p}}{\partial \bar{x}}\right)+\frac{\partial }{\partial \bar{z}}\left({\bar{h}}^3\bar{p}\frac{\partial \bar{p}}{\partial \bar{z}}\right)+12\eta \frac{p_a}{{\rho }_a}\rho \tilde{v}\\ =\text{2}\lambda \Lambda \frac{\partial \left(\bar{p}\bar{h}\right)}{\partial \tau }+\Lambda \frac{\partial }{\partial \bar{x}}\left(\bar{p}\bar{h}\right)\end{array}$ (4)

2.2. 数值分析

利用扰动理论将轴承的振动分为轴向扰动和径向扰动。建立气体静压轴承扰动模型，如图1所示，对于具有恒定转速的空气静压轴颈轴承，气膜压力和气膜厚度取决于轴颈中心位置一及其位置的变化率。

Figure 1. The disturbance diagram of the static pressure gas bearing

图1. 静压气体轴承的扰动示意图

$p=p_0+p_X\Delta X+p_{\stackrel{\dot{}}{X}}\Delta \stackrel{\dot{}}{X}+p_Z\Delta Z+p_{\stackrel{\dot{}}{Z}}\Delta \stackrel{\dot{}}{Y}$ (5)

$h=h_0+h_X\Delta X+h_{\stackrel{\dot{}}{X}}\Delta \stackrel{\dot{}}{X}+h_Z\Delta Z+h_{\stackrel{\dot{}}{Y}}\Delta \stackrel{\dot{}}{Z}$ (6)

为了解决方程(4)线性摄动方法是，假设期刊中心以小振幅周期运动的方式围绕其稳态位置旋转，旋转频率为ω_s。那么该中心的无量纲扰动位移可以表示为：

$\Delta \bar{X}=\left|\Delta X\right|{\text{e}}^{\text{i}{\omega }_{s}t}=\left|\Delta X\right|{\text{e}}^{\text{i}\tau }$ (7)

$\Delta \bar{Z}=\left|\Delta Z\right|{\text{e}}^{\text{i}{\omega }_{s}t}=\left|\Delta Z\right|{\text{e}}^{\text{i}\tau }$ (8)

对时间项求导：

$\frac{\partial \bar{p}}{\partial \tau }={\bar{p}}_X\Delta \stackrel{\dot{}}{X}-{\bar{p}}_{\stackrel{\dot{}}{X}}\Delta X+{\bar{p}}_Y\Delta \stackrel{\dot{}}{Y}-{\bar{p}}_{\stackrel{\dot{}}{Y}}\Delta Y$ (9)

$\frac{\partial \bar{h}}{\partial \tau }={\bar{p}}_X\Delta \stackrel{\dot{}}{X}-{\bar{p}}_{\stackrel{\dot{}}{X}}\Delta X+{\bar{p}}_Y\Delta \stackrel{\dot{}}{Y}-{\bar{p}}_{\stackrel{\dot{}}{Y}}\Delta Y$ (10)

气膜厚度的无量纲处理

$\bar{h}=1+Z\cos \varphi -X\sin \varphi$ (11)

将(9) (10) (11)代入(4)中求解雷诺方程，同时需要定义边界条件：

大气边界条件： $p\left(z=0\right)=p\left(z=nz+1\right)=p_a$

对称边界条件： $p\left(x=0\right)=p\left(nx+1\right)$

求解方程需要用牛顿迭代耦合非定常雷诺方程，利用超松弛迭代法满足边界条件和节流孔处的质量连续性方程，计算的压力分布提供了整合刚度和阻尼的系数，通过推导和坐标的变化可以得到刚度和阻尼。模型参数如表1所示：

Table 1. Small hole gas bearing parameters

表1. 小孔气体轴承参数

3. 特性参数分析

通过变换坐标和有量纲转化，求出动态特性刚度和阻尼。

$\left(\begin{array}{c}Kxx\\ Kyx\end{array}\right)=\frac{p_a{l}^2}{h_m}{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{\pi d/l}{\bar{p}}_X\left(\begin{array}{c}\sin \Delta \bar{x}\\ -\cos \Delta \bar{x}\end{array}\right)\Delta \bar{x}\Delta \bar{z}}}$ (12)

$\left(\begin{array}{c}Kxx\\ Kyx\end{array}\right)=\frac{p_a{l}^2}{h_m}{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{\pi d/l}{\bar{p}}_Y\left(\begin{array}{c}\sin \Delta \bar{x}\\ -\cos \Delta \bar{x}\end{array}\right)\Delta \bar{x}\Delta \bar{z}}}$ (13)

$\left(\begin{array}{c}Dxx\\ Dyx\end{array}\right)=\frac{p_a{l}^2}{h_m\omega }{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{\pi d/l}{\bar{p}}_{\stackrel{\dot{}}{X}}\left(\begin{array}{c}\sin \Delta \bar{x}\\ -\cos \Delta \bar{x}\end{array}\right)\Delta \bar{x}\Delta \bar{z}}}$ (14)

$\left(\begin{array}{c}Dyy\\ Dxy\end{array}\right)=\frac{p_a{l}^2}{h_m\omega }{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{\pi d/l}{\bar{p}}_{\stackrel{\dot{}}{Y}}\left(\begin{array}{c}\sin \Delta \bar{x}\\ -\cos \Delta \bar{x}\end{array}\right)\Delta \bar{x}\Delta \bar{z}}}$ (15)

通过轴承静特性求出无量纲承载力：

$\{\begin{array}{l}{\bar{W}}_x={\displaystyle {\sum }_i{\displaystyle {\sum }_j{\bar{p}}_x\Delta \bar{x}\Delta \bar{z}\sin \left(\frac{\left(i-0.5\right)\Delta \bar{x}}{R}\right)}}\\ {\bar{W}}_y={\displaystyle {\sum }_i{\displaystyle {\sum }_j{\bar{p}}_y\Delta \bar{x}\Delta \bar{z}\cos \left(\frac{\left(i-0.5\right)\Delta \bar{x}}{R}\right)}}\end{array}$ (16)

$\bar{W}=\sqrt{{\bar{W}}_x^2+{\bar{W}}_y^2}$ (17)

4. 结果分析

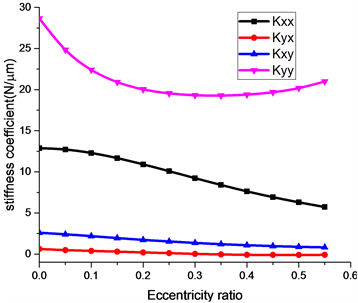
图2是显示了动态刚度和动态的变化在转速n = 5000 rpm，n_s = 5000 rpm情况下相对于偏心率的阻尼和刚度。从图2(a)中可以看出随着偏心的增加轴承的主刚度Kxx和Kyy是伴随着一定的下降，但是Kyy在随着偏心增大的过程中出现了先下降后上升的过程；这说明了提高Kyy可以采取利用大偏心来实现。这个原因是由于轴承的主要承载力是集中在轴承的径向方向，所以径方向的偏心是大于轴方向；也因此导致了径向方向的刚度是大于轴向方向，同时由于本章采取的是5孔双排计算模型，所以导致初始状态的刚度径向是大于轴向方向，而在交叉刚度Kxy和Kyx变化不明显，这是因为偏心的发生只是集中在竖直的径向方向，所以对轴向方向的压力变化也几乎没有太明显的影响。图2(b)是反映的阻尼随着偏心变化的情况，从图中可以看出随着偏心率的增加主阻尼Dyy是不断增加的，Dxx是略微的减小，对于偏心的不断增加，在径向方向的气膜厚度是逐渐减少，导致了Dyy的阻尼是不断增加，这是更气体的压缩性是有一定关系的，但是随着大偏心的出现会导致气膜厚度极薄，理论上气体刚度是为此一个恒定的值，这也是阻尼在大偏心下变化较小，同时由于偏心是在径向方向进行，对于偏心的反方向由于气膜厚度的增加会导致刚度的减小，阻尼的变小，气体的可压缩性变大，同样对于交叉阻尼Dxy,Dyx变化较小，这仍然是属于气膜厚度发生变化主要的是发生在径向方向。同时随着主阻尼Dyy增大，意味着轴承在运转的过程中更加的稳定。对于在小偏心范围内由于Dyy变化速率较不稳定因素较大。

图3显示了轴承动态刚度的变化在偏心率为0.4扰动转速n_s = 3000 rpm的情况下，对于轴承数的阻尼系数。可以看出情况下，轴承数(转速)对气体轴承的刚度和阻尼。图3(a)显示了轴承数(转速)对刚度的影响，同样可以明显的看出主刚度kyy是所有刚度中变化最明显，显示参数也最大，说明了随着轴承数(转速)的增大，轴承的动力学特性明显，对于交叉刚度kxx和kyy变化不明显。图3(b)是阻尼变化示意图，在图中可以看出随着轴承数(转速)的增加，主阻尼Dxx和Dyy都是不断减小其中Dyy减小较大，这是因为随着轴承数(转速)的增加，会导致气膜内部的压力产生一定变化，利用轴颈的剪切运动对气膜压力产生影响，所以随着转速的增加会导致期末区域内部的剪切运动加强，因此会导致主阻尼明显减小；对于交叉阻尼Dyx和Dxy同样是属于转速对影响，会导致在气膜内压力分布不均匀，从而导致了交叉刚度Dxy发生增加，Dyx减小。

(a)(b)

Figure 2. Stiffness and damping vary with eccentricity (n = 5000 rpm, n_s = 5000 rpm, h_m = 20 μm)

图2. 刚度和阻尼随着偏心率变化(n = 5000 rpm, n_s = 5000 rpm, h_m = 20 μm)

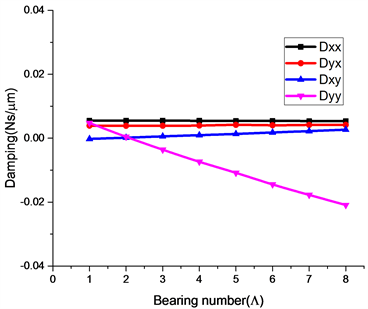(a) (b)

Figure 3. Stiffness and damping for different bearing counts (ε = 0.4, n_s = 3000 rpm, n = 3000 rpm, p_s = 6 atm)

图3. 不同轴承数的刚度和阻尼(ε = 0.4, n_s = 3000 rpm, n = 3000 rpm, p_s = 6 atm)

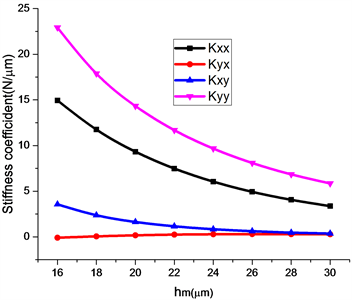
图4是偏心率在0.4的情况下气膜厚度的变化对刚度和阻尼的影响变化图，从图中可知主刚度Kxx和Kyy变化较为明显，出现了随着气膜厚度的逐渐增加，轴承的主刚度逐渐减小，这与空气动力学和热力学知识相符合，因为随着气体容量的增加，容积的压缩量也会增加，会导致刚性性质变弱，对于耦合交叉刚度Kxy和Kyx相对变化较小；同时随着气膜厚度逐渐增大，刚度逐渐减小，最后有逐渐趋于一个定值的趋势，这可能是由于转子的自身惯性作用所导致的，从图4(a)可以说明了平均气膜的增加对主刚度的Kxx和Kyy有较，也会导致高转速情况下出现失稳。从图4(b)中看出随着平均气膜厚度的增加，主阻尼Dxx和Dyy逐渐减小，并且减小的趋势较为明显，对于交叉耦合刚度的影响较小，这说明了平均气膜厚度的增加会增加轴承的振动效果，对于整个轴承转子系统的稳定性影响较大。综合图4可以说明，增加平均气膜对静压气体轴承高转速下的稳定性有不利的作用。

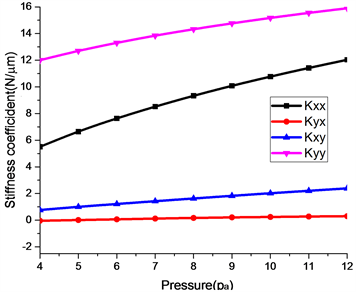
图5是供气压力对静压气体轴承的刚度和阻尼的影响，从图5(a)可以发现供气压力的不断的增大，主刚度Kxx和Kyy有明显的提高，交叉刚度Kyx和Kxy增加趋势较为缓慢，因此增加供气压力对提高静压气体轴承的刚度有明显的作用，同时对于提高轴承稳定性有重要的帮助。从图5(b)中可以发现在主阻尼Dxx和Dyy在变化过程中出现了交叉的现象，其中Dxx是随着供气压力的提高有逐渐减小的趋势，Dyy有逐渐增大的趋势，交叉阻尼Dyx和Dxy是有逐渐变小的趋势，这对于轴承在运转过程中减振有不利的影响，所以有一个合理的供气压力使气体静压轴承的减振状态最佳。

(a) (b)

Figure 4. Influence of average film thickness on stiffness and damping (ε = 0.4, p_s = 8 atm, n_s = 3000 rpm, n = 3000 rpm)

图4. 平均气膜厚度对刚度和阻尼的影响(ε = 0.4, p_s = 8 atm, n_s = 3000 rpm, n = 3000 rpm)

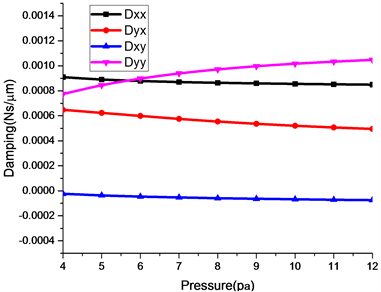(a) (b)

Figure 5. Effect of gas supply pressure on stiffness and damping (ε = 0.4, h_m = 20 μm, n_s = 3000 rpm, n = 3000 rpm)

图5. 供气压力对刚度和阻尼的影响(ε = 0.4, h_m = 20 μm, n_s = 3000 rpm, n = 3000 rpm)

图6是转速对静压气体轴承承载力的影响，通过图中可以看出在承载力在不同转速情况下有一定的变化，对于偏心率小于0.4情况下，不同转速情况下的承载力几乎一样，没有明显的区别，但是在偏心率大于0.4的情况下，承载力变化较为明显，同时转速越高，承载力变化越明显，对于低转速情况下的承载力变化同样不明显，因此在对高转速或者超高转速的气体轴承分析过程中，转速对气体轴承承载力的影响较大。

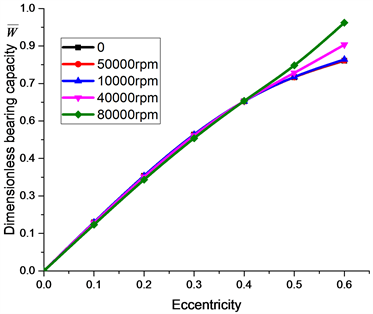
Figure 6. Change relation of bearing capacity

图6. 承载力变化关系

5. 结论

本文利用扰动理论提出轴向扰动和径向扰动对气体轴承的影响，通过求解非定常雷诺方程，得到径向节流小孔静压轴承的静动态特性，结论如下：

1) 随着偏心率的不断增加，气体轴承的两个主刚度有比较明显的减小趋势，且气体轴承的y向阻尼逐渐增大，x向阻尼变化不大。所以在偏心率较小的情况下，转速对承载力影响较小，随着偏心率的增大，转速对承载力的影响也逐渐显著。

2) 随着转速的不断增加，气体轴承竖直方向的刚度不断变大，但是竖直方向的阻尼不断变小。通过提高供气压力可以有效的提高轴承的刚度，但对轴承的阻尼影响较小。

3) 随着气膜厚度的增加，轴承的刚度和阻尼都在不断减小，并且减小的幅度逐渐降低，最终趋于一个定值。所以增大轴承的气膜厚度可以有效地提高空气静压轴承的承载力。

基金项目

国家自然科学基金(11562002)；广西自然基金(2015GXNSFAA139262)；广西研究生创新项目(GKYC201704)。

NOTES

^*通讯作者。