1. 引言
平板网架结构虽然在公共建筑领域由于新型空间结构型式的冲击而失去优势,但在设置悬挂吊车的工业建筑领域则占有垄断地位。在网架工业厂房中设置悬挂吊车作为起重设备可谓一大创新!其布置方式的灵活性和对生产工艺要求的适应性绝非传统桥式吊车可以相比。因此,平板网架结构在悬挂吊车工业建筑中的应用前景势必更加广阔!同时,悬挂吊车作用下的网架结构疲劳问题也成为热点难题。疲劳载荷谱是结构零部件疲劳设计、疲劳寿命预估、模拟实验、强度分析与计算以及可靠性设计的依据,也是经处理后获得的载荷–时间历程 [1] 。近些年来,虽然相关条文和规范标准中列入了关于疲劳的规定,然而,并没有建立载荷谱的先例。疲劳载荷谱的可靠性将直接影响部件寿命和疲劳强度的有效性。疲劳载荷谱的研究在整个疲劳问题的研究中起着重要作用 [2] 。对于网架结构,在文献 [3] [4] [5] 中已经研究了常福疲劳寿命的估算,但是对变幅疲劳寿命的估算较少。而且,实际上大多数部件的工作载荷是变幅载荷,因此研究变幅疲劳寿命估算非常重要。
2. 平板网架结构理论载荷谱编谱方法
高镇同院士曾在文献 [6] 中指出,“由于各种产品各异,且工作条件不同,载荷–时间历程的类型也各不相同,因此,应该针对所编谱的类型做出准备工作,并且不适合使用统一的方法。”由此,我们在编谱过程以及后续载荷谱实测中,应当把建筑结构构件的载荷谱编制方法独立考虑,且与当前研究的机械零件载荷谱的编制方法加以区分。而且,网架结构的载荷谱编制方法与其他建筑结构构件的编制方法也不尽相同。因此,当编制悬架起重机作用下的网格结构的悬挂点的疲劳载荷谱时,应充分考虑结构参数,所提供的悬吊起重机的特性以及所编谱的使用要求。从而选择一个科学合理的载荷谱编制方法。
因此,应考虑以下因素来编制悬挂吊点的载荷谱:
1) 网架的节点型式及结构型式;
2) 网架结构下设置悬挂吊车的使用情况,需了解吊车运行次数及运行频繁程度;
3) 与安装悬挂起重机有关的影响因素,如起重机类型、吊点数、吊点间距、吊点施工构造、工作级制、起重重量等;
4) 使用理论方法收集的数据的局限性;
5) 在平板网架结构中,悬挂吊点处载荷谱模拟方法的可行性。
本文所釆用的平板网架理论载荷谱编制方法以雷宏刚教授在文献 [7] 提出的总体框架为主,如图1所示。
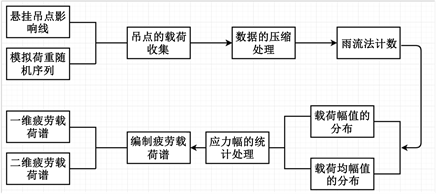
Figure 1. Overall framework for fatigue load spectrum compilation of plate grid structures
图1. 平板网架结构疲劳载荷谱编制的总体框架
3. 编谱过程
3.1. 平板网架模型的建立及其悬挂点载荷谱编制的准备
在本文中,以某平板网架结构为例,拟使用焊接空心球节点。LX型电动单梁悬挂起重机,工作起重机水平为A5,起重能力为5 t,跨度为12 m。
MSTCAD用于构建网格模型。设计的网格结构中有34个悬挂点。本文找到了起重机运行过程中34个吊点的载荷极值,或者受力影响严重的吊点,我们将其称之为控制吊点,并编制控制吊点的疲劳载荷谱。
根据选定的网格结构参数,模型和轨道布局见图2、图3、图4。
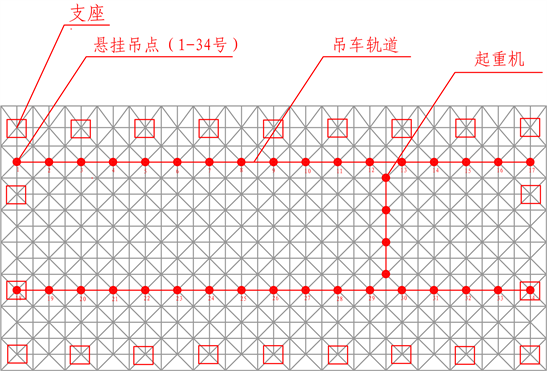
Figure 2. Layout of rail and lifting point of crane with flat grid structure
图2. 平板网架结构起重机轨道和提升点布局

Figure 3. Face-up diagram of welded hollow spherical joint flat grid structure
图3. 焊接空心球节点平板网架结构的正视图

Figure 4. Side view of welded hollow spherical joint flat grid structure
图4. 焊接空心球节点平板网架结构的侧视图
3.2. 建立平板网架结构模型
MIDAS作为土木结构专用的结构分析与优化设计软件,我们用其建立平板网架的有限元模型,并验算2.1节中MSTCAD确定的杆的截面是否满足要求。
模型建立如图5。
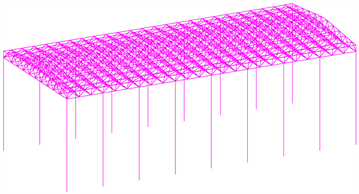
Figure 5. Construction of suspension point and support sketch of flat grid structure by MIDAS
图5. MIDAS建立平板网架结构吊点及支撑示意图
其中网架长48米,宽21米,网格高度为1.5米,网格尺寸为边长均为3米的矩形。弦周边支撑作为支撑方式,并提供22个支座支撑。起重机额定起重量为5 t,起重机重量为2.3 t,最大运行速度为30 m/min,履带车型为I20 a。提升点之间的距离为3米,提升点数为34个,钢构件均为Q345,目前悬挂起重机的吨位为1 t~10 t。由于平板网架的整体刚度过大,轨道提升点通常设计成铰接的。
3.3. 编制吊点疲劳载荷谱
根据吊点的布置示意图,共有34个悬挂点。没有必要对此34个悬挂点逐一进行疲劳载荷谱的编制,不仅耗费工作时间徒增工作任务,而且并不是所有的吊车悬挂点均具有代表性。它不能作为未来悬挂式起重机作用下平板网架结构疲劳载荷谱编制的参考 [8] [9] 。
文献 [10] [11] 中指出,只需找到起重机运行过程中34个悬挂吊点之中,受到载荷最大的吊点,或者受力影响最为严重的吊点,并编制此处的疲劳载荷谱。
为将疲劳载荷谱的理论研究成果和大量现场实测成果相结合,建立平板网架结构的悬挂吊车标准疲劳载荷谱,我们必须在仿真阶段尽可能充分考虑载荷谱在实测阶段将会出现的影响因素,例如吊车行进过程中的水平制动力、载荷的超载和欠载、外界温度等。但是有时候限元软件也难以考虑完全这些因素。为了使理论分析能够更加逼近于实际情况,我们在仿真过程中做出如下假设:
1) 在仿真过程中,暂不考虑水平制动力及其他外部作用力影响;
2) 起重机和重物作为悬挂轨道上的集中载荷,相当于静力计算的车轮压力值;
3) 起重机可在同一工作循环中保持恒定速度;
4) 将吊车轨道视作铰接的连续粱。
通过使用MIDAS进行分析和计算,在进行工作循环的过程中,当起重机承受全部提升重量时,为了找出控制吊点,我们将各悬挂吊点的最大载荷幅值进行统计,如表1所示。

Table 1. Maximum load amplitude statistics at hanging point (Unit: N)
表1. 吊点处的最大载荷幅值统计(单位:N)
在平板网架的34个悬挂吊点中,标号为9号的吊点承受的载荷幅值最大,其最大负载幅值为54368 N。因此,本文选择9号悬挂点作为编制对象。
在模拟期间,假设悬架起重机以30 m/min的均匀速度移动,并且在其操作过程中,对吊重荷载进行持续且随机地改变。为了研究悬挂提升点在随机提升载荷下的载荷-时间历程,假设起重机总是位于控制吊点处,并对其施加随机吊装载荷,编制不同吊装载荷下控制吊点的载荷–时间历程。对于本文研究的A5悬挂起重机,可以估计它每6分钟提升一次,平均每天工作4小时。在一周的第5天,可以估计本周悬挂的起重机数量约为200次。
因此,数学软件Mathcad用于生成5 t或更小的随机数和200个正态分布N。
由于在有限元分析软件MIDAS的计算中存在限制,我们得到的控制吊点的载荷谱仅仅适用于局限的工作情况之下。我们必须掌握需要编制载荷谱的控制吊点处在吊车全寿命下的工况,才能更加精确的推算出网架的疲劳残余寿命。根据文献 [12] [13] [14] ,悬挂起重机作用下的网架结构悬挂点的载荷幅值应符合正态分布。为检验作为样本的载荷幅值是否服从正态分布,需要先对其进行检验。
检验方法利用偏度–峰度检验,此方法实质是t-检验的两种独立方法,偏度检验的计算统计量记为式(1),峰度检验为式(2):
(1)
(2)
其中:
(3)
(4)
本文数理统计下,选取样本量为200,此样本来源于在控制吊点处,施加随机载荷下的载荷幅值,S = 8659.8,
。可求得,g1 = −0.05862,g2 = −0.93429。再将g1,g2,n分别代入t-检验,可得偏度检验结果为:
,峰度检验结果为:
。在两种检验结果下,可以得出,本文所选取的随机载荷具有有效性,并且载荷幅值所组成的200个样本是服从正态分布的,从而概率密度函数可以简化为如下公式:
(5)
有限元软件MIDAS用于求解所有随机载荷下9号提升点的载荷幅值,9号提升点的载荷–时间历程曲线绘制如图6。

Figure 6. Load-time history of No. 9 hanging point
图6. 9号悬挂吊点的载荷–时间历程
根据影响线的原理,在不同的提升载荷下,虽然9号提升点的载荷幅值会有所不同,但是,载荷–时间历程曲线的形状是一致的。
3.4. 绘制吊点频数直方图
标准疲劳载荷谱,直接影响到累计损伤理论估算疲劳寿命的准确性以及疲劳可靠度指标的确定,疲劳应力是结构工作过程中的连续随机过程,为了能够估算疲劳损伤值,我们可以借用雨流计数法将应力–时间历程变更为一组较为完整的循环加载。雨流计数通常在应力历程曲线上进行,应力和载荷呈现正比关系,之间仅有弹性模量的差异。而且,材料的弹性模量一般视为常数,由此认为应力与载荷是线性关系。因此,可以通过雨流计数方法计算负荷过程的平均值和幅值。文献 [15] 编制的雨流计数软件适用于处理控制吊点的加载时间历程,控制吊点的频率直方图如图7。

Figure 7. Frequency histogram of No. 9 hanging point
图7. 9号吊点的频数直方图
3.5. 绘制吊点的超值累积频数曲线
我们可以将提升点的超值累积频率曲线作为疲劳寿命估算的依据,为未来的网格结构的疲劳设计和疲劳寿命估算提供依据 [16] 。在上述吊点频率分布图的基础上,横坐标为超值累积频数,纵坐标为幅值的下限,将各点用平滑曲线相连,绘制控制吊点的累积频数曲线。控制吊点的累积频数表见表2。

Table 2. Control point 9 cumulative frequency Table
表2. 9号控制点累积频数表
在绘制超值累积频数曲线之前,为了能够简化曲线方程,可将曲线方程通过二项式拟合,结果计为:
控制吊点超值累积频数曲线如图8。
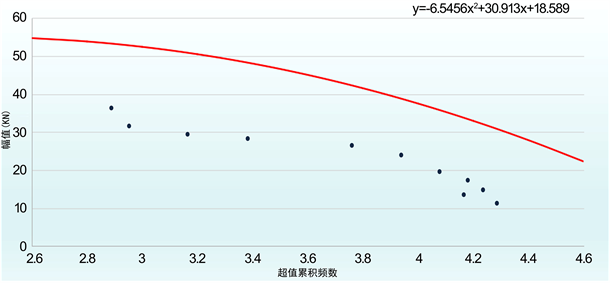
Figure 8. Overvalue cumulative frequency curve of No. 9 hanging point
图8. 9号吊点超值累积频数曲线
4. 结论
1) 通过有限元仿真,建立了焊接球节点平板网架在悬挂吊车作用下的模型,得到了平板网架结构在主要工况下吊点的载荷–时间历程;
2) 利用数理统计,得到了控制吊点的累积值频数曲线,为累计损伤理论估算疲劳寿命以及疲劳可靠度指标的确定提供参考。
3) 由于实际工程的多样性,吊车随机载荷的不确定性,本文仅作为理论疲劳载荷谱编制的参考,建立普遍适用的网架结构疲劳载荷谱还需要大量的现场实测工作。
基金项目
国家自然科学基金(51578357)资助。
NOTES
*第一作者。
#通讯作者。