1. 引言
1.1. 研究背景
参数为
的一个设计,简称t-设计,定义为符合以下条件的一对符号
:
1) X是一个v-集合;
2)
是X的一组k-子集;
3) X的任意给定的t-子集都恰好含于
的
个成员之中。
X的元素称为点,
的成员称为区组。若一个
设计不包含重复的区组,则称这个设计为单纯的。在本文中我们只考虑单纯t-设计。
令
,则对于任意的
,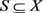 ,
。
称为S的轨道,
称为S的稳定子群,且
。
的一个自同构是指具有下述性质的X的置换g:如果
,则
。G是
的自同构群当且仅当区组集
是G作用下X的k-子集的轨道的并。
,
。
称为S的轨道,
称为S的稳定子群,且
。
的一个自同构是指具有下述性质的X的置换g:如果
,则
。G是
的自同构群当且仅当区组集
是G作用下X的k-子集的轨道的并。
令q为素数幂,
为射影直线。对任意的
,定义
, ,
,
。所有行列式为非零平方元的线性分式的集合构成线性分式群
,它同构于
。即
,
,
。所有行列式为非零平方元的线性分式的集合构成线性分式群
,它同构于
。即
.
设
,其中p为素数。利用
为设计的自同构群来研究t-设计是一个可行的方法。特别的,文献 [1] 已完整解决了以
为自同构群,区组长度为k的3-设计的存在性问题,其中
。文献 [2] [3] [4] [5] 完整讨论了以
为自同构群,区组长度为k (
)的单纯3-设计的存在性问题。文献 [6] [7] 介绍了以
为自同构群,区组长度为d和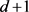 的单纯3-设计的有关结果,这里
。文献 [8] - [13] 找到了一些
时的t-设计存在的例子。
的单纯3-设计的有关结果,这里
。文献 [8] - [13] 找到了一些
时的t-设计存在的例子。
注意到当
时,对于任意的区组长度k总满足
。又
在X上的作用是精确3重传递的,故任意不相交的k-子集的轨道的并可构成单纯
设计,其中
为正整数。
本文只考虑
的情形。用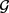 表示
,用
表示
,用 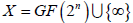 表示射影直线。总假设l为奇数,d为满足
且
的整数。利用
在X上作用的轨道,确定了以
为自同构群,区组长度为
,初始区组的稳定子群中含有d阶元的单纯3-设计的参数,并计算了满足这一参数的轨道的条数。得到了如下结果:
表示射影直线。总假设l为奇数,d为满足
且
的整数。利用
在X上作用的轨道,确定了以
为自同构群,区组长度为
,初始区组的稳定子群中含有d阶元的单纯3-设计的参数,并计算了满足这一参数的轨道的条数。得到了如下结果:
定理:令B为
中一个d阶元的2l个d圈及其一个不动点所构成的X的
-子集,则
构成一个
设计。构成这一设计的轨道的条数为
。
1.2. 预备知识
引理1 [14] :设
,g的阶为h且
,则g有a个不动点和
个h圈。其中当
时,
;当
时,
;当
时,
。
注:由引理1易知若B为X的一个k-子集,
当且仅当B由g的q个h圈和r个不动点构成,其中
,
。
引理2 [14] :
的一个非平凡子群必为下列之一:
1)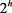 阶初等Abel群,其中
;
阶初等Abel群,其中
;
2) d阶循环群,其中
;
3) 二面体群
,其中
;
4)
阶的初等Abel群和d阶循环群的半直积,其中
;
5)
,其中
;
6) 交错群
。
引理3 [6] :类型(4)的子群不可能是2d阶的。
引理4 [14] :所有二面体群
在
中共轭。
以下总假设
且
,
为
中的一个d阶元,
,
,
,m为任意正整数,l为任意奇数。
引理5 [6] :
为一个二面体群
。
引理6 [7] :若S为一个
-子集,则无二面体群
包含在
中。
由引理6易得下面的推论。
推论1:若S为一个
-子集,则无二面体群
包含在
中。
证明:若存在一个二面体群
,由引理4及引理5知存在
,使得
。由引理1知
由
的m个d圈和1个不动点构成,则
中恰包含0和
中的一个元素。又因为
,由此推得若
必有
,产生矛盾。证毕。
引理7 [6] :若S为X的k-子集,则
是一个单纯
设计,其中
。
2 定理的证明
引理8:令B为
中一个d阶元的2l个d圈及其一个不动点所构成的X的
-子集,则
构成一个
设计。
证明:由于
中有d阶元,由引理2知
不为类型(1)。由推论1知
不为类型(3)。进一步的
不为类型(5),否则存在一个二面体群
包含在
中,与推论1矛盾。又类型(6)是类型(4)的一种情形,综上述
只能为类型(2)或类型(4)的子群。可设
,其中h为非负整数。由引理7知
为整数,又l是奇数,故
或1。再由引理3知
。故
构成一个
设计。
推论2:令S为X的
-子集,若
中有d阶元,则
为d阶循环群。
引理9:设S是X的
-子集,若
中有d阶元,则轨道
中包含形如
的区组。其中
为
中的一个d阶元,
(
)。
引理10:若
是一个
设计,则轨道
中包含m个形如
的区组。其中
为
中的一个d阶元,
(
)。
证明:设S为轨道
中的一个区组。由引理7得
,即d阶循环群。由引理9可设
.
若
与S位于同一条轨道,则存在
中的一个线性分式
,使得
。设
,
。由于
且
,从而
。又
,由此可得
。即
。对于
,若
,则对任意的
,有
。即
.
由上述等式知存在
,使得
.
故只能
,
且
。即
。可令
,其中
。因此
.
又
,令
,从而
或
,其中
。下分两种情况讨论:
1) 若
,从而
。
2) 若
,不失一般性,可令
,从而
.
故对于 1 ≤ k ≤ m−1,必存在
。即
.
令
Math_207#,其中
,则上述
。综上述若
当且仅当
Math_212#。
下证
互不相同。由此说明
中包含m个形如
的区组。对于任意的
,若
,则
,即
。从而
,即
.
这是不可能的。
引理11:构成
设计的轨道的条数为
。
证明:设l为奇数,
为
中的一个d阶元,
(
)。令
,易得
中元素的个数为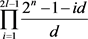 。再由引理10可得构成
设计的轨道条数为
。
。再由引理10可得构成
设计的轨道条数为
。
定理:令B为
中一个d阶元的2l个d圈及其一个不动点所构成的X的
-子集,则
构成一个
设计。构成这一设计的轨道的条数为
。
证明:利用引理8和引理11可以得到定理。
推论3:令B为
中一个d阶元的2l个d圈及其一个不动点所构成的X的
-子集,则对于任意的正整数t,其中
,可构造出单纯
设计。
致谢
衷心感谢导师李伟霞在本文写作过程中的悉心指导!
NOTES
*通讯作者。