1. 引言
本文考虑如下非凸非光滑优化问题:
(1)
其中
,
为正常下半连续函数,
连续可微。这一模型广泛应用于信号恢复、图像处理等问题。
求解问题(1)的常用方法是基于Gauss-Seidel迭代的交替极小化方法,迭代形式如下:
(2)
在凸的情况下, [1] 证明当
连续可微,且关于x或y严格凸时,序列
的每一个极限点都是
的稳定点。 [2] 通过引入正则项去掉了 [1] 中的严格凸条件,提出邻近交替极小化方法(PAM),迭代格式如下:
对于问题(1),本文在惯性思想的启发下,结合邻近交替极小化方法,提出一种惯性邻近交替极小化算法。惯性思想最早由Alvarez [3] 提出,用来解决动力系统问题。惯性思想是指为了得到下一步迭代点需要用到当前迭代点与上一步迭代点的信息,其优点是加快收敛速度。近年来,这一惯性类型的算法越来越受关注。如惯性向前向后分裂算法 [4] [5] ,惯性Douglas-Rachford 分裂算法 [6] ,惯性ADMM [7] 等。
2. 预备知识
本节列出本文用到的基本概念及性质。
设
,记
为满足如下条件的凹可微函数
的集合
(i)
;
(ii)
在
上连续;
(iii)
,
。
定义1 (Kurdyka-Lojasiewicz性质)设
是正常下半连续函数。
(i) 设
,若存在
,
的一个邻域U及
有
,
则称
在
处有Kurdyka-Lojasiewicz (KL)性质。
(ii) 若
在
中的每一点都满足KL性质,则称
为KL函数。
引理1 (一致Kurdyka-Lojasiewicz性质)设集合
是紧集,
是正常下半连续函数。若
在
上为常数,且在
的每一点处都满足KL性质。设
,则存在
使得
,
引理2 [8]
是连续可微函数,
Lipschitz连续(Lipschitz常数为L),则对任意
,有
3. 算法及假设条件
本文需要如下假设条件:
假设1 (i)
,
(ii) 对任意固定的y,
关于x是Lipschitz连续的,
为Lipschitz常数,即
(iii) 对任意固定的x,
关于y是Lipschitz连续的, 为Lipschitz常数,即
为Lipschitz常数,即

(iv) 存在
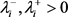 ,使得
,使得 ,
,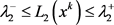 。
。
(v)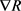 在
在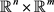 的有界子集上Lipschitz连续,即对任意有界集
的有界子集上Lipschitz连续,即对任意有界集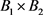 ,
,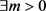 ,使得
,使得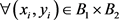 ,
,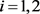 ,有
,有

惯性邻近交替极小化算法(IPAM):
步0. 给定初始点 ,选取
,选取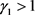 ,
, 。
。
步1. 令 ,计算
,计算
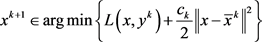 (3)
(3)
步2. 取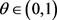 ,并计算
,并计算
 (4)
(4)
步3. 令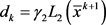 ,计算
,计算
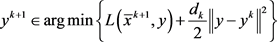 (5)
(5)
4. 收敛性分析
记 为惯性邻近交替极小化算法产生的序列。
为惯性邻近交替极小化算法产生的序列。
4.1. 充分下降性
引理3:若假设1成立,则
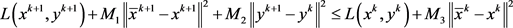 (6)
(6)
其中 ,
,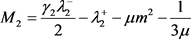 ,
, 。
。
证明:由(3),(5)知,
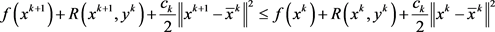 (7)
(7)
 (8)
(8)
由引理2得
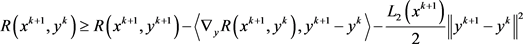

将上述不等式代入(7),(8)得
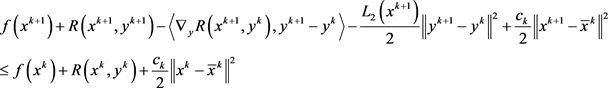

以上两式相加得
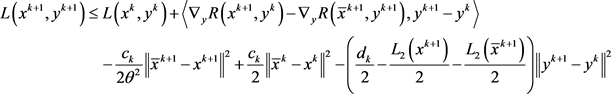
由不等式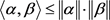 ,
,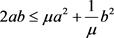 ,
,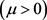 ,及假设(v)可知,
,及假设(v)可知,
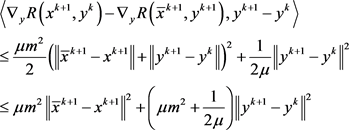
进一步由 ,
, 及假设(ii),得
及假设(ii),得
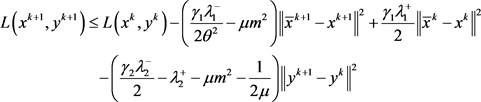
移项后可证得(6)式成立。
注1. 若参数 满足下列不等式条件
满足下列不等式条件
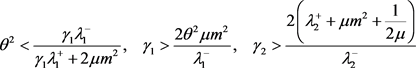
则有 ,且
,且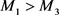 。
。
注2. 记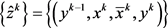 ,
, 。则有
。则有
 (9)
(9)
其中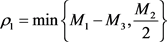 。
。
4.2. 次微分的范数估计
引理4:若假设1成立, 有界,令
有界,令

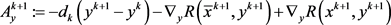
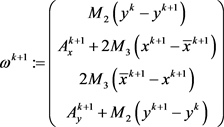 (10)
(10)
则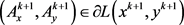 ,
, 。更进一步,存在常数
。更进一步,存在常数 ,使得
,使得
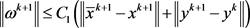
证明:由最优性条件可知,

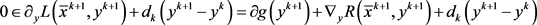
因此,


根据函数H的定义,得

故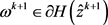 。
。
由假设1(v),得

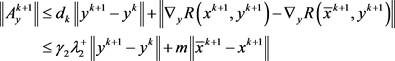
因此,存在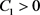 ,使得
,使得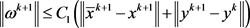 。
。
引理5:若假设1成立, 有界,则
有界,则 。
。
证明:由假设1(i)知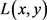 有下界,故
有下界,故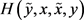 也有下界,再由注2,
也有下界,再由注2, 非增。根据单调有界定理可知,
非增。根据单调有界定理可知, 收敛,其极限为
收敛,其极限为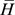 。
。
令N为正整数,将(9)式从 到相加
到相加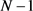 ,得
,得

令N趋于无穷,得

故 ,
, 。
。
又
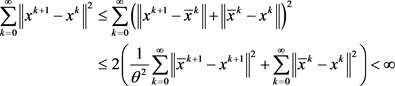
因此, 。
。
4.3. 收敛结论
记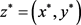 为序列
为序列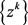 的一个极限点,
的一个极限点, 。
。
定理1:设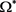 为序列
为序列 的极限点集。若假设1成立,
的极限点集。若假设1成立,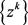 有界,则有以下结论成立
有界,则有以下结论成立
(i) 是非空紧的连通集,且
是非空紧的连通集,且 ,
,
(ii)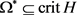 ,
,
(iii) 当且仅当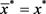 时,
时, ,
,
(iv)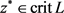 ,
,
(v) H在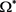 上恒为常数。
上恒为常数。
证明:(i) 证明可参照文献 [9] 引理5。
(ii) 对任意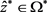 ,则存在一个子序列
,则存在一个子序列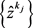 ,有
,有 。由f的下半连续性,有
。由f的下半连续性,有 。
。
再由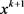 的定义得,
的定义得,

取 ,有
,有
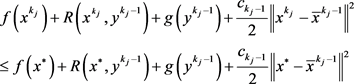 (11)
(11)
在引理5的证明中得, 。
。
而 ,对(11)式中的
,对(11)式中的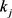 取上极限,得
取上极限,得 。因此,
。因此, 。同样地,
。同样地,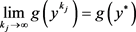 。根据R的连续性,
。根据R的连续性, 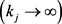
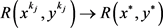 。故
。故
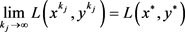

由引理4及(10)知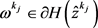 ,
, (
(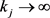 )。再由
)。再由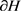 的闭性,有
的闭性,有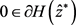 。因此,
。因此, 。
。
(iii) 由引理5及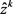 的定义,结论得证。
的定义,结论得证。
(iv) 由引理4及引理5知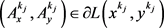 ,
,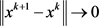 ,
, 。则
。则 (
(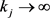 ),再由
),再由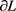 的闭性,有
的闭性,有 ,即
,即 。
。
(v) 记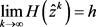 ,(h为常数)。对任意
,(h为常数)。对任意 ,则存在一个子序列
,则存在一个子序列 ,使得
,使得 。再根据(iii)证明过程中所得
。再根据(iii)证明过程中所得 。于是,
。于是,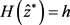 ,即H在
,即H在 上恒为常数。
上恒为常数。
定理2:假设H是Kurdyka-Lojasiewicz函数, 有界,则
有界,则
(i)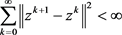 ,
,
(ii)序列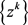 收敛到L的一个稳定点
收敛到L的一个稳定点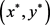 。
。
证明:由定理1,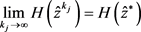 ,
,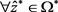 。接下来,将分成两种情况证明。
。接下来,将分成两种情况证明。
Case1. 存在一个正整数 ,使得
,使得 。由注2知
。由注2知 ,
, ,则
,则 ,
, 。于是,定理得证。
。于是,定理得证。
Case2. 对所有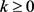 ,有
,有 。根据极限的定义,由
。根据极限的定义,由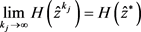 ,则对给定
,则对给定 ,
, ,
, ,使得当
,使得当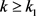 时,有
时,有 。由定理1(i),即对给定
。由定理1(i),即对给定 ,
, ,
, ,使得当
,使得当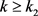 时,有
时,有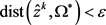 。于是,对给定
。于是,对给定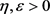 ,有
,有 ,
,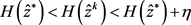 ,
, 。
。
(i) 由引理1,则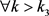 ,有
,有
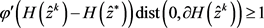
由 的凹性,
的凹性,
 (12)
(12)
记 。利用注2,结合(12)式,有
。利用注2,结合(12)式,有

移项后,不等号两边同时开方,根据不等式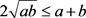 得
得
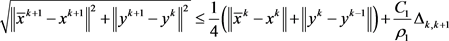 (13)
(13)
再由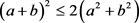 得
得

将(13)式代入上式,得

将上式从 相加得
相加得
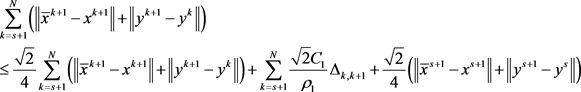
因为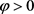 ,则
,则

于是,

令N趋于无穷,得

故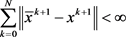 ,
,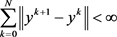 。
。
于是,
 ,
,
因此,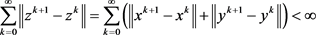 。
。
(ii) 由(i)可知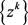 为柯西序列,故收敛。由定理1,可知
为柯西序列,故收敛。由定理1,可知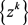 收敛到L的一个稳定点。
收敛到L的一个稳定点。
5. 数值试验
为了验证算法的有效性与可行性,本节应用惯性邻近交替极小化算法(IPAM)及邻近交替极小化算法(PAM)求解 问题。数值试验过程均由MATLAB(2014a)实现,程序运行环境为:Windows 7 (64 bite),RAM:4G,CPU:@ 1.60 GHz 2.30 GHz。
问题。数值试验过程均由MATLAB(2014a)实现,程序运行环境为:Windows 7 (64 bite),RAM:4G,CPU:@ 1.60 GHz 2.30 GHz。
在压缩感知中,基础的问题是从m个不完全实验数据中恢复一个n维的稀疏信号x,(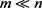 )。该问题可转化为如下模型:
)。该问题可转化为如下模型:

或正则化形式
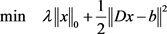
其中 是实验矩阵,
是实验矩阵, 是观察信号,
是观察信号,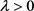 是正则化参数,
是正则化参数, 表示x中非零元素的个数。一般情况下,上述模型是NP难问题。为了克服这一困难,可以用
表示x中非零元素的个数。一般情况下,上述模型是NP难问题。为了克服这一困难,可以用 拟范数来松弛
拟范数来松弛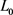 问题,考虑下述问题
问题,考虑下述问题

其中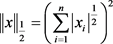 。通过引入一个新的变量
。通过引入一个新的变量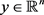 ,将问题转化为带约束的问题
,将问题转化为带约束的问题

再用罚函数方法将上述问题转化为问题(1)的形式
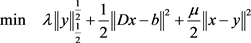 (14)
(14)
利用IPAM求解问题(14),有

其中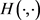 被称为half-shrinkage算子 [10] 。
被称为half-shrinkage算子 [10] 。
利用PAM求解问题(14),有
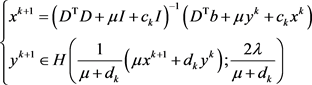
在试验过程中,选取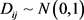 ,并正则化每一列,随机生成含有100个非零元素的稀疏向量
,并正则化每一列,随机生成含有100个非零元素的稀疏向量 ,每一个样本都服从正态分布。向量
,每一个样本都服从正态分布。向量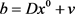 ,其中
,其中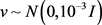 ,正则化参数
,正则化参数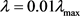 ,其中
,其中 。选取参数如下:
。选取参数如下: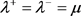 ,
,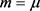 ,
, ,
,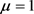 ,
, ,
, 。除
。除 外的其他参数,两种算法选取相同的参数值。终止准则为
外的其他参数,两种算法选取相同的参数值。终止准则为
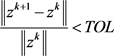
 为给定的误差值。计算两种算法在不同情况下分别所需的迭代次数,迭代时间及目标函数值。由图1可知,IPAM与PAM目标函数都趋于一个固定值,说明两种算法都收敛。且由表1知,IPAM比PAM运行时间更少,收敛速度更快。
为给定的误差值。计算两种算法在不同情况下分别所需的迭代次数,迭代时间及目标函数值。由图1可知,IPAM与PAM目标函数都趋于一个固定值,说明两种算法都收敛。且由表1知,IPAM比PAM运行时间更少,收敛速度更快。

Figure 1. The trend of objective function varies with iterations
图1. 目标函数随迭代次数变化趋势
基金项目
获国家自然科学基金青年基金(No. 1160195),国家自然科学基金(No. 71861002),广西自然科学基金青年基金(2017GXNSFBA380185),(2017GXNSFBA198238)资助。
NOTES
*通讯作者。