科技进步伴随节约的资源开采模型

doi:10.12677/SD.2019.93063

期刊菜单

科技进步伴随节约的资源开采模型
Resource Exploitation Model under Technological Progress and Resource Saving

DOI: 10.12677/SD.2019.93063, PDF, HTML, XML,
作者: 崔惠鹏：太原市农机局，山西太原
关键词: 科技进步；资源节约；资源开采模型；常微分方程；Technological Progress； Resource Saving； Resource Exploitation Model； Ordinary Differential Equation

摘要: 随着科技不断进步，人类对不可再生资源的开采速度不断增加。在开采过程中，又不断加强对资源的节约。考虑到人类资源最终将枯竭，本文建立了一个模型来描述地球资源在科技进步和资源节约共同作用下的开采趋势。通过建立模型得出每个时期资源的开采趋势，包括剩余资源总量、当期开采量、已开采资源量，并进行了模拟。

Abstract: Along with the unceasing technical progress, the exploitation rate of non-renewable resources by human is increasing. In the process of exploitation, the conservation of resources is increasing. Considering that human being resources will eventually be exhausted, this paper establishes a model to describe the exploitation trend of earth resources under the combined action of techno-logical progress and resource conservation. Through the establishment of the model, the exploita-tion trend of resources in each period is obtained, including the total amount of remaining re-sources, the exploitation amount in the current period and the total amount of exploited resources. And the simulation is made.

文章引用：崔惠鹏. 科技进步伴随节约的资源开采模型[J]. 可持续发展, 2019, 9(3): 536-540. https://doi.org/10.12677/SD.2019.93063

1. 引言

本文的资源指煤、石油、天然气等不可短时间内再生成的资源，即不可再生资源。当今世界，随着科技的飞速发展，人类对资源的开采日益增加。同时，为了减少资源消耗，保持可持续发展，人们也在加强对资源的节约。科技发展、技术进步会导致资源的开采越来越快，而不断加强的节约又会延缓资源的开采速度。这个过程中，必将存在一个资源开采的增加期、最高点和减少期，直至资源最终枯竭。

为了描绘这种趋势，本文通过建立数学模型，来寻求在科技进步和资源节约共同作用下，地球资源开采的规律或者说总体开采趋势。目前，现有的研究都是从文字的角度阐述科技进步与资源的关系，或者是提倡节约资源。并未见有用数学模型来描述科技进步和节约对资源的影响。

2. 建立模型

科技进步对不可再生资源的影响是：随着时间的发展，人类对资源的开采速度增加。设t时期不可再生资源的剩余总量为 $R (t)$ ，t时期的当期资源开采量为 $E (t)$ 。同索罗模型 [1] ，设t时期的科技 $A (t) = A (0) \cdot e^{g \cdot t}$ ，因此可取当期资源开采量 $E (t)$ 与时间t也呈指数变化。又由于开采过程将导致资源存量 $R (t)$ 减少，伴随着资源存量的减少，人类会逐步加强对资源的节约。因此可取：

$E (t) = E (0) \cdot e^{m \cdot t} \cdot \frac{R (t)}{R_{0}}$ ( $E (0) > 0, m > 0$ ) (1)

$R_{0}$ 为初始资源量。乘以 $\frac{R (t)}{R_{0}}$ 可以理解为，随着资源存量的减少，当期开采量与加强的节约成反比。 $R (t)$ 又等于初始资源量 $R_{0}$ 减去0至t时期的资源开采量总数 $\int_{0}^{t} E (t) d t$ ，即：

$R (t) = R_{0} - \int_{0}^{t} E (t) d t$ (2)

将(2)式代入(1)式得：

$E (t) = E (0) \cdot e^{m \cdot t} \cdot \frac{R_{0} - \int_{0}^{t} E (t) d t}{R_{0}}$ ( $E (0) > 0, R_{0} > 0, m > 0$ )(3)

再设0至t时期的资源开采量总数为 $T (t)$ ，即：

$T (t) = \int_{0}^{t} E (t) d t$ (4)

以上(2)、(3)、(4)式完成模型描述。下一节求解模型中的 $E (t)$ 、 $R (t)$ 、 $T (t)$ 。

3. 模型求解

通过求解(3)式，可以得到 $E (t)$ 关于时间t的一个函数。设 $y \equiv T (t) = \int_{0}^{t} E (t) d t$ ，则 $y^{'} = E (t)$ ，代入到(3)式得：

，

化简为：

$y^{'} + \frac{E (0)}{R_{0}} \cdot e^{m \cdot t} \cdot y = E (0) \cdot e^{m \cdot t}$ (5)

常数变易法解此常微分方程(5)：

$y^{'} + \frac{E (0)}{R_{0}} \cdot e^{m \cdot t} \cdot y = 0$ $\Rightarrow \frac{d y}{y} = - \frac{E (0)}{R_{0}} \cdot e^{m \cdot t} d t$ $\Rightarrow \ln | y | = - \frac{E (0)}{R_{0}} \cdot \frac{1}{m} \cdot e^{m \cdot t} + C_{1}$

$\Rightarrow y = C \cdot e^{- \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}}$

常数变易： $y = u (t) \cdot e^{- \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}}$ ，代入到方程(5)得：

$u^{'} (t) \cdot e^{- \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} = E (0) \cdot e^{m \cdot t}$ $\Rightarrow u^{'} (t) = e^{m \cdot t + \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} \cdot E (0)$

$\Rightarrow u (t) = E (0) \cdot \int e^{m \cdot t + \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} d t + C_{2}$ (6)

又：

$E (0) \cdot \int e^{m \cdot t + \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} d t = \frac{E (0)}{m} \cdot \int e^{\frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} {de}^{m \cdot t} = R_{0} \cdot \int e^{\frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} d \frac{E (0)}{R_{0} \cdot m} e^{m \cdot t} = R_{0} \cdot e^{\frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}}$ ，

代入到(6)式得：

$u (t) = R_{0} \cdot e^{\frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} + C_{2}$ ，

则由常数变易：

$y = u (t) \cdot e^{- \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} = (R_{0} \cdot e^{\frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} + C_{2}) \cdot e^{- \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} = R_{0} + C_{2} \cdot e^{- \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}}$

再由(2)、(4)式得：

$R (t) = R_{0} - T (t) = R_{0} - y = - C_{2} \cdot e^{- \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}} = C_{3} \cdot e^{- \frac{E (0)}{R_{0} \cdot m} \cdot e^{m \cdot t}}$ (7)

当 $t = 0$ 时， $R (t) = R_{0}$ ，代入到(7)式解得： $C_{3} = R_{0} \cdot e^{\frac{E (0)}{R_{0} \cdot m}}$ ，则t时期剩余的资源总量为：

$R (t) = R_{0} \cdot e^{\frac{E (0)}{R_{0} \cdot m} (1 - e^{m \cdot t})}$ ( $E (0) > 0, R_{0} > 0, m > 0$ ) (8)

将 $R (t)$ 代入(1)式，得t时期的当期资源开采量为：

$E (t) = E (0) \cdot e^{m \cdot t + \frac{E (0)}{R_{0} \cdot m} (1 - e^{m \cdot t})}$ ( $E (0) > 0, R_{0} > 0, m > 0$ ) (9)

且从0至t时期的资源开采量总数为：

$T (t) = R_{0} - R (t) = R_{0} \cdot (1 - e^{\frac{E (0)}{R_{0} \cdot m} (1 - e^{m \cdot t})})$ (10)

以上(8)、(9)、(10)式完成模型求解。

4. 模拟分析

对模型中的 $R (t)$ 、 $E (t)$ 进行模拟，因 $T (t) = R_{0} - R (t)$ ，即 $T (t)$ 与 $R (t)$ 变化趋势相反，因此 $T (t)$ 未在图中进行模拟。模拟结果如图1。

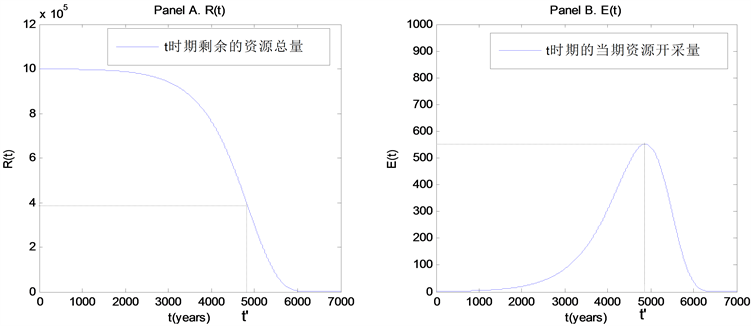
Figure 1. Curve: remaining amount and current exploitation amount of non-renewable resources in period t

图1. t时期不可再生资源的剩余量和当期开采量

$R (t)$ 为t时期剩余的不可再生资源的总量， $E (t)$ 为t时期的当期资源开采量。图1中的Panel A为 $R (t)$ 随时间变化的趋势，Panel B为 $E (t)$ 随时间变化的趋势。取初始值 $R_{0} = 10^{6}$ ， $E (0) = 1$ ， $m = 0.0015$ 。改变初始参数值，可以得出不同的数据结果，但是图像趋势是相同的。

由图1中可见，存在 $t^{'}$ 时期，在 $t^{'}$ 时期当期资源开采量 $E (t)$ 取最大值，剩余资源总量 $R (t)$ 处于拐点处。 $R (t)$ 值始终呈减少趋势。当剩余资源总量 $R (t)$ 减少至0时，当期资源开采量 $E (t)$ 也减少至0，此时煤、石油、天然气等不可再生资源将开采完。改变模型中的初始参数值，可以得出不同的数据结果，但是图像趋势是相同的。改变初始参数值，并且参照已有的矿产开采数据，可以对未来矿产资源的开采程度进行一定的预测。由于存在较多不确定因素，我们并不能确定目前的地球资源开采处于模型中的哪一个时期，本文只是通过模型给出一个总体的资源开采趋势。

5. 总结

不可再生资源终将耗尽，人们最终将依靠可再生资源生存，可再生资源指太阳能、风能、核能等不会枯竭的资源。本文提出了一个科技进步伴随节约的资源开采模型。本模型揭示了在科技进步以及资源节约的共同作用下，地球上矿产等不可再生资源的开采趋势。参照此模型，可以预测矿产资源未来的开采趋势。本模型对于资源的开采具有一定的参考意义。通过本文，也在于给人类提出警示，不可再生资源的开采量将遵循模型中的趋势并直至枯竭，在资源枯竭之前，我们应加大对可再生能源的利用。以及如何加大开发和利用可再生能源，更应该及早规划。

参考文献

[1]	戴维罗默, 著. 高级宏观经济学[M]. 第三版. 王根蓓, 译. 上海: 上海财经大学出版社, 2009: 9-10.

为你推荐

友情链接