PC[0,1]的共轭空间

Conjugate Space of PC[0,1]

摘要: 本文基于连续函数空间的共轭空间的构造方法，通过Stieltjes积分理论，得到了区间上具有有限个间断点，在间断点处仅左连续且右极限存在的函数全体所成空间的共轭空间。随后给出区间上具有无限个间断点，在间断点处仅左连续且右极限存在的函数全体所成空间的共轭空间。

Abstract: Based on the construction method of conjugate space of continuous function space and Stieltjes integral theory, this paper obtains the conjugate space of the PC[0,1] space in which the functions has finite discontinuous points, has right limit at discontinuity points and is left continuous at discontinuity points. Finally, we get conjugate space of the PC[0,1] space in which the functions has infinite discontinuous points, has right limit at discontinuity points and is left continuous at dis-continuity points also.

1. 引言

$PC\left[0,1\right]$ 空间是指在 $\left[0,1\right]$ 区间上具有有限个间断点，在间断点处函数左连续且右极限存在的函数构成的空间，即：

$PC\left[0,1\right]$ = { $x:\left[0,1\right]\to R|\exists s_1,s_2\cdots s_m\in \left(0,1\right)$， $x\left(s\right)$ 在 $s\ne s_i$ 时连续，在 $s=s_i$ 时，有 $\underset{s\to s_i-}{\lim }x\left(s\right)=x\left(s_i\right)$，且 $\underset{s\to s_i+}{\lim }x\left(s\right)$ 存在有限}，该空间范数定义为 $\Vert x\Vert ={\sup }_{t\backslash \text{in}\left[0,1\right]}\left|x\left(t\right)\right|$。

该类空间常见于脉冲微分方程研究中，见 [1] [2] [3] 。另一方面，Banach空间的共轭空间提供了认识原空间的新工具，其确立极为重要，比如由此派生的强拓扑、弱拓扑乃至弱*拓扑的概念，见文献 [4] [5] 。众多数学工作者对空间及其共轭空间的构造做了很多的研究，也取得了很多成果，见参考文献 [6] [7] [8] [9] 。本文将对 $\left[0,1\right]$ 区间上具有有限个间断点，且在间断点处左连续且右极限存在的函数全体构成的空间- $PC\left[0,1\right]$ 空间的共轭空间进行研究，然后对 $\left[0,1\right]$ 区间上具有无限个间断点，且在间断点处左连续且右极限存在的函数全体构成的空间的共轭空间进行论述。

2. 基础知识

首先，根据参考文献 [10] ，给出区间 $\left[0,1\right]$ 上的全变差函数及有界变差函数的定义及性质。

定义1.1 [10] ：设f为定义在区间 $\left[0,1\right]$ 上的函数，考察区间 $\left[0,1\right]$ 上的任意一组分点： $T:0=t_0<t_1<\cdots <t_{n-1}<t_n=1$。对于任一组分点，称上确界 $\sup \left\{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|f\left(t_i\right)-f\left(t_{i-1}\right)\right|}\right\}$ 为函数f区间 $\left[0,1\right]$ 上的全变差(全变分)，记为 $\underset{0}{\overset{1}{{\displaystyle \vee }}}\left(f\right)$。

定义1.2 [10] ：设f为定义在区间 $\left[0,1\right]$ 上的函数，考察区间 $\left[0,1\right]$ 上的任意一组分点 $T:0=t_0<t_1<\cdots <t_{n-1}<t_n=1$。若对任意分划T，变差 $\underset{0}{\overset{1}{{\displaystyle \vee }}}\left(f\right)=\underset{T}{\sup }\left\{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|f\left(t_i\right)-f\left(t_{i-1}\right)\right|}\right\}$ 都不超过某个正常数，即存在正数M，使得对一切分划T，有 $\underset{0}{\overset{1}{{\displaystyle \vee }}}\left(f\right)\le M$ 成立，则称函数f为区间 $\left[0,1\right]$ 上的有界变差函数。

定义1.3 [10] ：设 $V\left[0,1\right]$ 为 $\left[0,1\right]$ 区间上的有界变差函数的全体，它按照通常的线性运算及范数 $\Vert f\Vert =\left|f\left(0\right)\right|+\underset{0}{\overset{1}{{\displaystyle \vee }}}\left(f\right)$， $\left(f\in V\left[0,1\right]\right)$ 成为赋范线性空间。

定理1.1 [10] ：若f为区间上的有界变差函数，则f在区间 $\left[0,1\right]$ 上有界。

其次，根据参考文献 [5] ，给出同构映射及保范同构映射的定义。

定义1.4 [5] ：对于线性空间 $V,V^{\prime }$，若映射f具有以下性质：

1) f为双射；

2) $f\left(a+b\right)=f\left(a\right)+f\left(b\right),\forall a,b\in V$ ；

3) $f\left(ka\right)=kf\left(a\right),\forall k\in P,\forall a\in V$。

则称f是V到 $V^{\prime }$ 的同构映射，并称线性空间V与 $V^{\prime }$ 同构，记作 $V\cong V^{\prime }$。

保范同构映射则是在同构映射的前提下要求保证映射前后的范数相等，即要求一个线性映射将一个空间中的线性泛函一对一的映射到另外一个赋范线性空间，而且映射后的元素的范数和映射前的线性泛函的范数相等。

定义1.5 [5] ：设X和Y是两个赋范线性空间，T是X到Y中的线性算子，并且对X中所有的x，有 $\Vert Tx\Vert =\Vert x\Vert$ 成立，则称T是X到Y中的保距算子。如果T又是映射到Y上的，则称T是同构映射，称X与Y同构。

事实上，等距同构的两个空间除了符号不同之外，在结构上无法区别，在这种意义上也称这两个空间相等。

然后，根据参考文献 [11] ，给出Hahn-Banach定理的内容。

定理1.2 [11] ：设 $\kappa$ 是赋范线性空间，是 $\kappa$ 的线性子空间， $f_0$ 是定义在 ${\kappa }_0$ 上的有界线性泛函，那么空间 $\kappa$ 上必有一个有界线性泛函f，满足

1) (保范条件)；

2) $f\left(x\right)=f_0\left(x\right),\forall x\in \kappa$ (延拓条件)；

其中， ${\Vert f_0\Vert }_0$ 表示 $f_0$ 在 ${\kappa }_0$ 上的范数。

由于f满足(1)，(2)两个条件，通常称f为 $f_0$ 的保范延拓。

3. PC空间的共轭空间

定义

$BV\left[0,1\right]=\{g|g:\left[0,1\right]\to R,g\left(0\right)=0,g\left(t\right)=g\left(t+0\right),\forall t\in \left[0,1\right),\mathrm{var}\left(g\right)<\infty \},$

其中， $\mathrm{var}\left(g\right)=\sup {\displaystyle \sum \left|g\left(t_{j+1}\right)-g\left(t_j\right)\right|}$。

在空间 $BV\left[0,1\right]$ 上赋以范数 ${\Vert g\Vert }_v=\mathrm{var}\left(g\right)$， $\forall g\in BV\left[0,1\right]$，则有空间 $BV\left[0,1\right]$ 是完备的赋范线性空间。

定理2.1： $PC{\left[0,1\right]}^{\text{*}}=BV\left[0,1\right]$。即：

1) 对 $BV\left[0,1\right]$ 空间中的任一函数 $g\left(t\right)$，其对应于空间 $PC\left[0,1\right]$ 上的一个线性连续泛函 $\phi \mapsto \langle f,\phi \rangle ={\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}$ ；

2) 对空间 $PC{\left[0,1\right]}^{\text{*}}$ 中的任意函数f，必在空间 $BV\left[0,1\right]$ 中存在唯一的函数g，使得对空间 $PC\left[0,1\right]$ 中的任意函数 $\phi$，满足 $\langle f,\phi \rangle ={\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}$ 及 $\Vert f\Vert ={\Vert g\Vert }_v$。

证明：

第一步：证明对 $BV\left[0,1\right]$ 空间中的任一元素g，其对应于空间 $PC\left[0,1\right]$ 上的一个线性连续泛函 $$。

对空间 $BV\left[0,1\right]$ 中的任一元素g，对于 $PC\left[0,1\right]$ 空间内的任意元素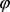，由定义，函数 $\phi$ 在 $\left[0,1\right]$ 区间上有界，即 $\exists M>0$，使得 $\left|\phi \left(t\right)\right|<M$， $\forall t\in \left[0,1\right]$ 成立。从而有函数 $\phi$ 在区间 $\left[0,1\right]$ 上的振幅 $\omega =\sup \phi \left(t\right)-\inf \phi \left(t\right)\le 2M$。

已知函数 $\phi \left(t\right)$ 在区间 $\left[0,1\right]$ 上有有限个间断点： $s_1,s_2,\cdots ,s_m$。对于区间 $\left[0,1\right]$ 上的任意分割 $T:0=t_0<t_1<t_2<\cdots <t_n=1$ $\left(n>2m\right)$。在其分割成的n个小区间： $\left[t_0,t_1\right],\left[t_1,t_2\right],\cdots ,\left[t_{n-1},t_n\right]$ 中，至多有2m个小区间含有间断点。于是将振幅和分成两部分

${\displaystyle \underset{k=1}{\overset{n}{\sum }}{\omega }_k\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]}={\displaystyle \sum \text{'}{\omega }_k\text{'}\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]\text{'}}+{\displaystyle \sum \text{'}\text{'}{\omega }_k\text{'}\text{'}\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]\text{'}\text{'}},$

其中， $$ 是相应于分割T中含有间断点的那些小区间的振幅和，其项数至多为2m项。 ${\displaystyle \sum \text{'}\text{'}{\omega }_k\text{'}\text{'}\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]\text{'}\text{'}}$ 是相应于分割T中不含有间断点的那些小区间的振幅和。

由定理1.1，函数g有界，即 $\exists h>0$， ${\Vert g\Vert }_v\le h$。于是对任意的 $t_i,t_j\in \left[0,1\right]$，有成立。因为 ${\displaystyle \sum \text{'}{\omega }_k\text{'}\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]\text{'}}$ 的项数至多为2m项，故对 $\forall \epsilon >0$， $\exists {\delta }_1>0$，且 ${\delta }_1<\frac{\epsilon }{16mhM}$，当 $\Vert T\Vert <{\delta }_1$ 时，有

${\displaystyle \sum \text{'}{\omega }_k\text{'}\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]\text{'}}\le {\displaystyle \sum \text{'}2M\left[g\left(t_k\right)-g\left(t_{k+1}\right)\right]}\le 2M\cdot 2h\cdot 2m{\delta }_1<8mhM\cdot \frac{\epsilon }{16mhM}=\frac{\epsilon }{2}.$

在 ${\displaystyle \sum \text{'}\text{'}{\omega }_k\text{'}\text{'}\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]\text{'}\text{'}}$ 所对应的小区间上，函数 $\phi$ 连续，从而一致连续。故 $\forall \epsilon >0$， $\exists {\delta }_2>0$，当 $\Vert T\Vert <{\delta }_2$ 时，可以保证函数 $\phi$ 在这些小区间的振幅都小于 $\frac{\epsilon }{4h}$。于是有

${\displaystyle \sum \text{'}\text{'}{\omega }_k\text{'}\text{'}\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]\text{'}\text{'}}<{\displaystyle \sum \text{'}\text{'}\frac{\epsilon }{4h}\left[g\left(t_k\right)-g\left(t_{k+1}\right)\right]\text{'}\text{'}}<\frac{\epsilon }{4h}\cdot 2h=\frac{\epsilon }{2}.$

因此，取 $\delta =\min \left\{{\delta }_1,{\delta }_2\right\}$，对于区间 $\left[0,1\right]$ 的任一分割T，只要 $\Vert T\Vert <\delta$，有

${\displaystyle \underset{k=1}{\overset{n}{\sum }}{\omega }_k\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]}={\displaystyle \sum \text{'}{\omega }_k\text{'}\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]\text{'}}+{\displaystyle \sum \text{'}\text{'}{\omega }_k\text{'}\text{'}\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]\text{'}\text{'}}<\frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon .$

故可得积分存在。

由Stieltjes积分，定义 ${\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}=\underset{\Vert T\Vert \to 0}{\lim }{\displaystyle \underset{i=0}{\overset{n-1}{\sum }}\phi \left(t_j^{\ast }\right)\left[g\left(t_{j+1}\right)-g\left(t_j\right)\right]}$，。从定义可见，对 $BV\left[0,1\right]$ 空间中的任一元素g，定义 $\langle f,\phi \rangle ={\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}$。

显然，有

$\langle f,k\phi \rangle ={\displaystyle {\int }_0^{1}k\phi \left(t\right)\text{d}g\left(t\right)}=k{\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}=k\langle f,\phi \rangle ,$

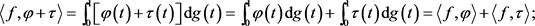
其中，k为数域P中任一元素， $\phi ,\tau \in \left[0,1\right]$。即可得 $\langle f,\phi \rangle ={\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}$ 为一连续线性泛函。由 $\langle f,\phi \rangle =\left|{\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}\right|\le \left|{\displaystyle {\int }_0^1\text{d}g\left(t\right)}\right|\Vert \phi \Vert$，可得 $\Vert f\Vert \le {\displaystyle {\int }_0^1\left|\text{d}g\left(t\right)\right|}=\mathrm{var}\left(g\right)={\Vert g\Vert }_v$。所以有 ${\Vert g\Vert }_v\ge \Vert f\Vert$。

第二步：证明对空间 $PC{\left[0,1\right]}^{\text{*}}$ 中的任意元素f，必在空间 $BV\left[0,1\right]$ 中存在唯一的元素g，使得对空间 $PC\left[0,1\right]$ 中的任意元素 $\phi$，成立 $\langle f,\phi \rangle ={\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}$，且有 ${\Vert g\Vert }_v\le \Vert f\Vert$。

定义 $E_s=\left[0,s\right]$，令函数 $\phi$ 为间断的特征函数，即

考虑区间 $\left[0,1\right]$ 上全体有界函数所成空间 $L^{\infty }\left[0,1\right]$。显然，空间 $PC\left[0,1\right]$ 是空间 $L^{\infty }\left[0,1\right]$ 的一个闭子空间。对空间 $PC\left[0,1\right]$ 中任意的元素 $$，有 $\phi \in L^{\infty }\left[0,1\right]$。

根据定理1.2，对于空间 $PC{\left[0,1\right]}^{\text{*}}$ 中任一元素f，必存在空间 $L^{\infty }{\left[0,1\right]}^{\ast }$ 中的元素F，使得 $\langle F,{\chi }_{E_0}\rangle =0$，且对空间 $PC\left[0,1\right]$ 中任意的函数 $\phi$，成立 $\langle F,\phi \rangle =\langle f,\phi \rangle$，并且有 $\Vert F\Vert =\Vert f\Vert$。

由定义，可知 ${\chi }_{E_s}\in L^{\infty }\left[0,1\right]$，所以有 $g\left(s\right)=\langle F,{\chi }_{E_s}\rangle ,\left(0<s\le 1\right)$， $g\left(0\right)=0$。

以下证明上述定义的函数 $g\in BV\left[0,1\right]$，并且满足 ${\Vert g\Vert }_v\le \Vert f\Vert$。

对区间 $\left[0,1\right]$ 上的任意分割 $T:0=t_0<t_1<\cdots <t_n=1$。记

${\varpi }_k=g\left(t_{k+1}\right)-g\left(t_k\right),k=0,1,\cdots ,n-1;$

${\lambda }_k=\{\begin{array}{l}0,{\varpi }_k=0\\ \mathrm{sgn}\left({\varpi }_k\right),{\varpi }_k\ne 0\end{array},k=0,1,\cdots ,n-1;$

于是，我们有

${\displaystyle \underset{k=0}{\overset{n-1}{\sum }}\left|{\varpi }_k\right|}={\displaystyle \underset{k=0}{\overset{n-1}{\sum }}{\lambda }_k{\varpi }_k}=\langle F,h\rangle \le \Vert F\Vert {\Vert h\Vert }_{L^{\infty }\left[0,1\right]}=\Vert F\Vert =\Vert f\Vert .$

即可得出 $g\in BV\left[0,1\right]$，并且满足 ${\Vert g\Vert }_v\le \Vert f\Vert$。

以下证 $$ 成立。

对于空间 $PC\left[0,1\right]$ 上的任意元素 $\phi$，对任意的 $\epsilon >0$，取分割T，保证 $PC\left[0,1\right]$ 空间内的元素 $\phi$ 的间断点都位于分点处，则对任意 $t,t^{\prime }\in \left(t_j,t_{j+1}\right)$， $j=0,1,\cdots ,n-1$，成立 $\left|\phi \left(t\right)-\phi \left(t^{\prime }\right)\right|<\frac{\epsilon }{2\Vert F\Vert }$。

由积分存在性，可得 $\left|{\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}-{\displaystyle \underset{j=0}{\overset{n-1}{\sum }}\phi \left(t_j^{\ast }\right)\left[g\left(t_{j+1}\right)-g\left(t_j\right)\right]}\right|<\frac{\epsilon }{2}$， $t_j^{\ast }\in \left(t_j,t_{j+1}\right)$，令 $\varphi ={\displaystyle \underset{j=0}{\overset{n-1}{\sum }}\phi \left(t_j^{\ast }\right){\chi }_{\left(t_j,t_{j+1}\right]}}+\phi \left(0\right){\chi }_{\left(0\right)}$。可得

$\begin{array}{l}\left|\langle f,\phi \rangle -{\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}\right|\le \left|\langle f,\phi \rangle -\langle F,\varphi \rangle \right|+\left|\langle F,\varphi \rangle -{\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}\right|\\ \le \Vert F\Vert {\Vert \phi -\varphi \Vert }_{L^{\infty }\left[0,1\right]}+\left|{\displaystyle \underset{j=0}{\overset{n-1}{\sum }}\phi \left(t_j^{\ast }\right)\left[g\left(t_{j+1}\right)-g\left(t_j\right)\right]}-{\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}\right|<\frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon \end{array}$

由 $\epsilon$ 的任意性，即得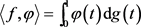成立。

以下证明g的唯一性。

不妨假设存在 $BV\left[0,1\right]$ 空间中的两个元素 $g,g_1$，成立 $\langle F,\phi \rangle ={\displaystyle {\int }_0^1\phi \text{d}g}={\displaystyle {\int }_0^1\phi \text{d}{g}_1}$。即有 ${\displaystyle {\int }_0^1\phi \text{d}\left(g-g_1\right)}=0$，由函数 $\phi$ 的任意性，可得函数g与 $g_1$ 是几乎处处相等的函数。

即证唯一性。

综上， $g\mapsto {\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}$ 是空间 $BV\left[0,1\right]$ 到空间 $PC{\left[0,1\right]}^{\text{*}}$ 的一个等距同构，即有 $PC{\left[0,1\right]}^{\text{*}}=BV\left[0,1\right]$。证毕。

以下针对 $\left[0,1\right]$ 区间上具有无限个间断点，且在间断点处函数左连续且右极限存在的函数构成的空间(仍记为 $PC\left[0,1\right]$ )的共轭空间进行研究论述。

$\begin{array}{l}PC\left[0,1\right]=\{x:\left[0,1\right]\to R|\exists s_1,s_2,\cdots ,s_m,\cdots \in \left(0,1\right),有\underset{m\to \infty }{\lim }{s}_m=1,x\left(s\right)在s\ne s_i时连续,\\ 在s=s_i时,有\underset{s\to s_i-}{\lim }x\left(s\right)=x\left(s_i\right),\underset{s\to s_i+}{\lim }x\left(s\right)极限存在,且有\underset{s\to 1}{\lim }x\left(s\right)=x\left(1\right)\}\end{array}$

定理2.2： $PC{\left[0,1\right]}^{\text{*}}=BV\left[0,1\right]$。

证明：

对于 $PC\left[0,1\right]$ 空间内的任意元素 $\phi$，对空间 $BV\left[0,1\right]$ 中的任一元素g，由定义，函数 $g\left(t\right)$ 在 $\left[0,1\right]$ 区间上有界，即 $\exists h>0$，使得 $$， $\forall t\in \left[0,1\right]$ 成立。

对任意正数 $\epsilon$，由函数 $\phi$ 在 $\left[0,1\right]$ 区间上有无限多个间断点： $s_1,s_2,\cdots ,s_m,\cdots$，且由 $\underset{m\to \infty }{\lim }{s}_m=1$ 及 $\underset{s\to 1}{\lim }x\left(s\right)=x\left(1\right)$，可知，存在足够小的正数 $\delta$，在 $\left[1-\delta ,1\right]$ 上，有 ${\varpi }_0\mathrm{var}\left(g\right)<\frac{\epsilon }{2}$。

在区间 $\left[0,1-\delta \right]$ 上，函数 $\phi$ 仅有有限个间断点，由定理2.1可知，积分 ${\displaystyle {\int }_0^{1-\delta }\phi \left(t\right)\text{d}g\left(t\right)}$ 存在。故对区间 $\left[0,1-\delta \right]$ 上的任意分割 $T:0=t_0<t_1<\cdots <t_n=1-\delta$，有振幅和 ${\displaystyle \underset{T}{\sum }{\omega }_k\left[g\left(t_k\right)-g\left(t_{k-1}\right)\right]}<\frac{\epsilon }{2}$。

因此将分割T与区间右端点1合成 $\left[0,1\right]$ 区间上一个新的分割 $T^{\prime }$，则对于区间 $\left[0,1\right]$ 上的分割 $T^{\prime }$，有振幅和

${\displaystyle \underset{T^{\prime }}{\sum }{\omega }_k\left[g\left(t_k\right)-g\left(t_{k+1}\right)\right]}={\displaystyle \underset{T}{\sum }{\omega }_k\left[g\left(t_k\right)-g\left(t_{k+1}\right)\right]}+{\omega }_0\left[g\left(1-\delta \right)-g\left(1\right)\right]<\frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon .$

即可得积分 ${\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}$ 存在。

根据Stieltjes积分，定义 ${\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}=\underset{\Vert T\Vert \to 0}{\lim }{\displaystyle \underset{i=0}{\overset{n-1}{\sum }}\phi \left(t_j^{\ast }\right)\left[g\left(t_{j+1}\right)-g\left(t_j\right)\right]}$， $t_j^{\ast }\in \left(t_j,t_{j+1}\right)$。从定义可见，对 $BV\left[0,1\right]$ 空间中的任一函数 $g\left(t\right)$，其对应于空间 $PC\left[0,1\right]$ 上的一个线性连续泛函 $\langle f,\phi \rangle ={\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}$。使其满足 $\Vert f\Vert \le {\displaystyle {\int }_0^1\left|\text{d}g\left(t\right)\right|}=\mathrm{var}\left(g\right)={\Vert g\Vert }_v$。所以有。

以下证明对空间 $PC{\left[0,1\right]}^{\text{*}}$ 中的任意元素f，必在空间 $BV\left[0,1\right]$ 中存在唯一的元素g，使得对空间 $PC\left[0,1\right]$ 中的任意元素 $\phi$，成立及 ${\Vert g\Vert }_v=\Vert f\Vert$。

证明过程同定理2.1一致，在此不予详证。

综上， $g\mapsto {\displaystyle {\int }_0^1\phi \left(t\right)\text{d}g\left(t\right)}$ 是空间 $BV\left[0,1\right]$ 到空间 $PC{\left[0,1\right]}^{\text{*}}$ 的一个等距同构，即有 $PC{\left[0,1\right]}^{\text{*}}=BV\left[0,1\right]$。证毕。