摘要:
本文通过Ψ(x)的n阶导数,给出了广义Ramanujan常数R(a,c-a)=-2γ-Ψ(a)-Ψ(c-a)的不同类型的级数展开式,这些级数展开式可以改进
R(a,c-a)的一些已知结果。
Abstract:
In this paper, the authors present several kinds of series expansion expressions of generalized Ramanujan constant R(a,c-a)=-2γ-Ψ(a)-Ψ(c-a) by the nth order derivative of Ψ(x). By these results, some known results about R(a,c-a) can be easily improved.
1. 引言
在本文中,对于正实数x和y,Γ-函数、B-函数以及ψ-函数分别定义 [1] 为:
(1.1)
令
,是Euler-Mascheroni常数,则
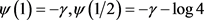 (1.2)
(1.2)
在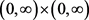 上定义Ramanujan常数 [2] [3] [4] 为:
上定义Ramanujan常数 [2] [3] [4] 为:
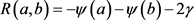 (1.3)
(1.3)
当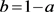 时,式(1.3)记为
时,式(1.3)记为
 ,
,
结合式(1.2)~(1.3)知 。
。
当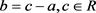 时,式(1.3)记为
时,式(1.3)记为
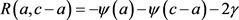 (1.4)
(1.4)
另外,Rieman-zeta函数
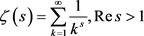 (1.5)
(1.5)
对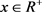 ,
,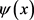 有下面一些常用到的等式:
有下面一些常用到的等式:
 (1.6)
(1.6)
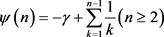 (1.7)
(1.7)
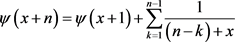 (1.8)
(1.8)
 (1.9)
(1.9)
 (1.10)
(1.10)
 .
.
众周所知,Ramanujan常数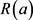 在零平衡的高斯超几何函数的研究中有着重要的应用,在特殊函数的一些其他领域也是必不可少的。而高斯超几何函数在特殊函数中有着极为重要的地位,与很多类型的特殊函数相关,它的性质和Γ-函数、B-函数以及ψ-函数密切相关,在研究这些函数的性质时经常用到Ramanujan常数
在零平衡的高斯超几何函数的研究中有着重要的应用,在特殊函数的一些其他领域也是必不可少的。而高斯超几何函数在特殊函数中有着极为重要的地位,与很多类型的特殊函数相关,它的性质和Γ-函数、B-函数以及ψ-函数密切相关,在研究这些函数的性质时经常用到Ramanujan常数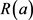 ,而
,而 的级数展开是重要而有效的研究工具 [5] [6] [7] [8] 。但目前
的级数展开是重要而有效的研究工具 [5] [6] [7] [8] 。但目前 的一些已知性质主要考虑的是
的一些已知性质主要考虑的是 的情况,本文的主要目的是建立广义Ramanujan常数
的情况,本文的主要目的是建立广义Ramanujan常数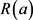 (即
(即 的情形)的不同类型的级数展开。
的情形)的不同类型的级数展开。
2. 主要结果
本节给出主要结果,本节出现的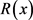 均是
均是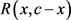 。
。
首先,建立广义Ramanujan常数 在
在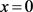 点处的级数展开。
点处的级数展开。
定理2.1. 设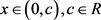 ,广义Ramanujan常数
,广义Ramanujan常数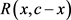 有如下的级数展开式:
有如下的级数展开式:
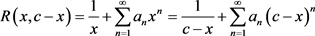 (2.1)
(2.1)
其中,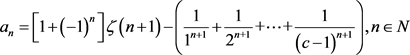 。
。
下面的定理中给出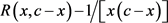 的级数展开式。
的级数展开式。
定理2.2. 设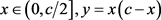 ,则
,则 有如下的级数展开式:
有如下的级数展开式:
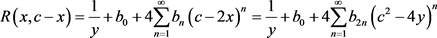 ,(2.2)
,(2.2)
其中,
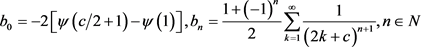 .
.
下面的定理中,我们将 展开成
展开成 的级数。
的级数。
定理2.3. 设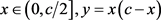 ,则
,则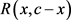 有如下的级数展开式:
有如下的级数展开式:
 , (2.3)
, (2.3)
其中,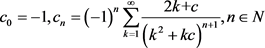 。
。
3. 主要结果的证明
本节给出定理2.1~2.3的证明。
定理2.1的证明:令
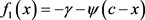 ,则
,则 ,
, ,且
,且
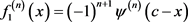 ,
,
根据式(1.5)和(1.9)可知,
 ,
,
于是,
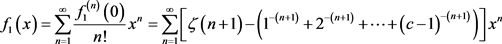 (3.1)
(3.1)
另外,由式(1.7)可知:
 (3.2)
(3.2)
有:
 (3.3)
(3.3)
由式(3.2)、(3.3)可得,

由 可得出第二个等式
可得出第二个等式
 .
.
定理2.2的证明:令
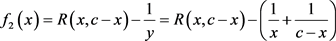
由式(1.4)及(3.3)可将 写成如下形式:
写成如下形式:
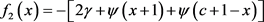 (3.4)
(3.4)
当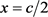 时,式(3.4)化为
时,式(3.4)化为
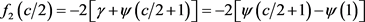 ,
,
对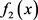 求n阶导数,则
求n阶导数,则
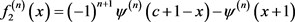 ,
,
由式(3.4)和(1.9)可知:
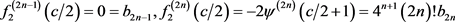 (3.5)
(3.5)
因此,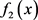 在
在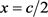 处有如下的级数展开式:
处有如下的级数展开式:
 .
.
由此可得式(2.2)中的第一个等式。根据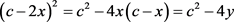 可得式(2.2)中第二个等式。
可得式(2.2)中第二个等式。
定理2.3的证明:令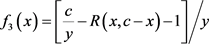 ,
,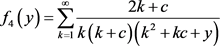 ,
,
易知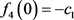 。由式(1.4)知,
。由式(1.4)知,
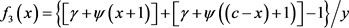 (3.6)
(3.6)
根据式(3.3)及 ,
, 可以写成
可以写成
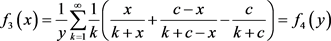 (3.7)
(3.7)
对 求n阶导数,可得
求n阶导数,可得
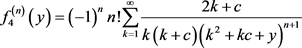 (3.8)
(3.8)
其中
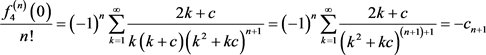 .
.
结合式(3.8), 有如下的级数展开式:
有如下的级数展开式:
 (3.9)
(3.9)
由式(3.9),可直接证得等式(2.3)。
基金项目
浙江省教育厅科研基金项目(Y201635387),浙江机电职业技术学院科研项目(A027117021),浙江机电职业技术学院课堂教学改革项目(A015219393),浙江省高等学校访问学者项目(FX2018093)。
NOTES
*通讯作者。