一种城市旅游业评价因素的确定方法

A Method for Determining the Evaluation Factors of Urban Tourism

摘要: 主成分分析是多元数据分析中的一个重要的简化算法的方法，SPSS是一种统计分析软件。基于主成分分析方法，利用SPSS对不同城市的旅游影响因素进行有关数据分析和数据处理，构造相关评价指数，并进行聚类分析，得出不同城市的不同旅游需求和消费特点等比较符合实际的结论，给旅游业管理部门提供了一种思路。

Abstract: Principal Component Analysis (PCA) is an important simplified algorithm in multivariate data analysis. SPSS is statistical analysis software. Based on the principal component analysis method, this paper uses SPSS to analyze and process the relevant data of tourism influencing factors in different cities, constructs the relevant evaluation index, and carries out cluster analysis. It draws a conclusion that the different tourism demand and consumption characteristics of different cities are in line with the actual situation, which provides a train of thought for tourism management and development departments.

1. 引言

近年来随着经济的不断发展，居民对旅游的需求程度在不断上涨。对不同省份和不同城市的相关旅游影响参数进行分析，从而对旅游地区进行综合评价，有利于管理者挖掘旅游潜力，提高旅游地区的管理水平 [1] [2] [3]。目前，应用统计学进行影响旅游影响因素分析的研究还不多见。付志伟以浙江省11个地级市为直接研究对象，分别从旅游资源基础条件、旅游业发展外部条件和旅游经济效应进行了比较分析，并对部分因子进行定量计算和排序 [4]。俞彤以广东省21个地级市为研究对象，从旅游产业竞争力、旅游资源竞争力和旅游企业综合竞争力等三方面选取了14个指标构建评价体系，对广东省城市旅游竞争力进行比较研究 [5]。李创新等采用多指标综合评价的主成分分析法进行区域旅游竞争力的定量分析，并按测评结果对各个省区进行了排序 [6]。刘欣从产业综合竞争力角度出发，在AHP分析法的基础上，根据相关研究成果及河北省区域特征，使用SPSS软件研究全国省际旅游业的竞争力发展水平的地区差异 [7]。

SPSS是IBM公司推出的一系列用于统计学分析运算、数据挖掘、预测分析和决策支持任务的软件产品及相关服务的总称，应用于自然科学、技术科学、社会科学的各个领域。其基本功能包括数据管理、统计分析、图表分析、输出管理等，统计分析过程包括均值比较、回归分析、时间序列分析、多重响应等，分析结果清晰直观，并且软件操作简单 [8] [9] [10] [11]。本文采用主成分分析方法，通过SPSS软件系统，采集有关数据，进行主成分分析，构造旅游城市的评判指数，得出比较符合实际的结论，给旅游业管理和开发部门提供了一种研究思路。

2. 基本理论

2.1. 主成分分析

主成分分析是多元数据分析中的一个重要方法，是在力保数据信息损失最小的原则下，对高维变量空间进行降维处理，达到简化算法的目的 [12]。

假设X是一个 $n\times m$ 变量的矩阵，即

$X={\left(x_{ij}\right)}_{n\times m}=\left[\begin{array}{c}{e}_1^{\text{T}}\\ e_2^{\text{T}}\\ ⋮\\ e_n^{\text{T}}\end{array}\right]=\left[x_1,x_2,\cdots ,x_m\right]$ (1.1-1)

设综合变量 $F_1$ 为 $x_1,x_2,\cdots ,x_m$ 的线性组合，即

$F_1=X{a}_1,a_1\in R^m,\Vert a_1\Vert =1$ (1.1-2)

要使得 $F_1$ 能携带最多的原变异信息，即要求 $F_1$ 的方差取到最大值，即

$\max a_1^{\text{T}}V{a}_1$ (1.1-3)

采用拉格朗日算法求解，得

$V{a}_1={\lambda }_1{a}_1$ (1.1-4)

最终得到

$\mathrm{var}\left(F_1\right)=a_1^{\text{T}}{\lambda }_1{a}_1={\lambda }_1$ (1.1-5)

$a_1$ 所对应的特征值 ${\lambda }_1$ 应该取到最大值。这里 $a_1$ 被称为第一主轴， $F_1=X{a}_1$ 被称为第一主成分。按照同样方法求得第二主轴 $a_2$ ，第三轴 $a_3$ ，……，第h个主轴 $a_h$ 对应的最优化问题，且

$\mathrm{var}\left(F_1\right)\ge \mathrm{var}\left(F_2\right)\ge \cdots \ge \mathrm{var}\left(F_n\right)$ (1.1-6)

利用数据变异大小来反映数据的信息，则 $F_1$ 携带的信息最大，如果选取m个主轴，则此m个主轴所携带的信息的总和为 ${\displaystyle {\sum }_{h=1}^m{\lambda }_h}$ 。

2.2. 精度分析

通过数据变量的方差反映主成分新构造出的主超平面包络的原数据。方差越大，所包含的信息就越多。定义累积贡献率 $Q_m$ 来反映主超平面的近似质量。

$Q_m=\frac{{\displaystyle {\sum }_{h=1}^m\mathrm{var}\left(F_h\right)}}{{\displaystyle {\sum }_{j=1}^m{s}_j}}$ (1.2-1)

其中 ${\displaystyle {\sum }_{h=1}^m\mathrm{var}\left(F_h\right)}$ 是m维主超平面上变量方差的总和， ${\displaystyle {\sum }_{j=1}^m{s}_j}$ 是原数据的变量方差总和。由于 $\mathrm{var}\left(F_h\right)={\lambda }_h$ ，1.2.1式可以简写成

$Q_m=\frac{{\displaystyle {\sum }_{h=1}^m{\lambda }_h}}{{\displaystyle {\sum }_{j=1}^m{s}_j}}$ (1.2-2)

当原数据经过标准化处理，得出

$Q_m=\frac{1}{m}{\displaystyle {\sum }_{h=1}^m{\lambda }_h}$ (1.2-3)

2.3. 聚类分析

聚类分析是将个体或对象分类，使得同一类的对象之间的相似性更比其他类对象之间的相似性更强，是对数据可视化的一种辅助手段。聚类的方法有许多种，在本文中，采用的聚类方法是动态聚类中的K-均值聚类法。

2.3.1. 闵可夫斯基距离

对于 $n\times m$ 的数据矩阵，即数据具有n维样本点，每个样本点对应m维数据点。令 $X_i=\left[a_{i1},a_{i2},\cdots ,a_{im}\right]$ ，则样本 $X_i$ 与样本 $X_j$ 的闵氏距离可以表现为

$D\left(X_i,X_j\right)={\left(\underset{k=1}{\overset{m}{{\displaystyle \sum }}}{\left|a_{ik}-a_{jk}\right|}^q\right)}^{\frac{1}{q}}$ (1.3-1)

其中q为某一自然数，当q取以下值时，是闵氏距离的特殊形式。

当 $q=1$ 时， $D\left(X_i,X_j\right)={\displaystyle {\sum }_{k=1}^m\left|a_{ik}-a_{jk}\right|}$ ，称为绝对值距离。

当 $q=2$ 时， $D\left(X_i,X_j\right)={\left({\displaystyle {\sum }_{k=1}^m{\left|a_{ik}-a_{jk}\right|}^2}\right)}^{\frac{1}{2}}$ ，称为欧式距离，也是本文中采用的距离处理。

当 $q=\infty$ 时， $D\left(X_i,X_j\right)=\max \left(1\le k\le m\right)\left|a_{ik}-a_{jk}\right|$ ，成为切比雪夫距离。

2.3.2. K-均值聚类

K-均值聚类法是有麦奎因(Mac Queen, 1967)提出并命名的一种聚类方法，其思想是把每个样品划归到重心(均值)与其最接近的那个类，其基本步骤如下：

选取k个样品作为初始聚类点；或将所有样品点初始分为K类，将每类的重心作为初始聚类点；将除了初始聚类点意外的所有样本点进行归类，将每个样本点计算与初始聚类点的闵氏距离，距离最小的归为一类，分为K类；将新的一类重新计算中心记为下一次的聚类点，重复以上步骤，直到达到聚类的要求为止。

3. 构造城市旅游业评价指数模型

3.1. 样本点采集

挑取了北京、上海、厦门、天津、深圳、广州、杭州等35个国内典型的旅游城市作为样本点进行分析，主要考虑的因素包括旅游人数、景区数(5A级景区数、4A级景区数)、垃圾处理率、城市公园数量、城市公园绿化面积、城市旅游业收入等7项数据。

3.2. 构造评价指数模型

经过归类分析，认为：1) 一个城市高等级的景区数量对旅游业起到主要作用，所以用城市的4A级景区和5A级景区的数量总和合成城市景区数量总值，作为一个评价指标。2) 城市景区的拥挤程度是目前旅游人群考虑的重要因素，所以用旅游的总人数/景区数量表示在旅游期内平均每个景区所容载的旅游人群数量，构造为拥挤指数。3) 城市的环境，主要包括绿化、卫生、垃圾处理以及其他公共设施对旅游人群影响较大，所以对垃圾处理率、城市公园数量、以及绿化面积赋予一定的比值来构造生态指数，反映一个城市的环境。4) 旅游费用是旅客在旅游中考虑的一项重要因素，用旅游总收入/旅游人数来表示旅游的人均旅游消费，构造出一个城市旅游的消费指数。具体构造方式如下：

景区总数 = 5A级景区数 + 4A级景区数。

拥挤指数 = 旅游人数/景区数。

生态指数 = 垃圾处理率*α + 城市公园数量*β + 城市公园的绿化面积*γ。

人均消费 = 城市旅游业收入/旅游人数。

4. 利用SPSS对相关因素处理分析

4.1. 主成分分析

利用SPSS对四个评判指数进行主成分分析操作，提取两个主成分，可以得到表1、表2、图1相关信息。

Table 1. Explanation of total variance

表1. 总方差解释

提取方法：主成分分析法。

Table 2. Component trix a

表2. 成分矩阵^a

提取方法：主成分分析法。

^a提取了2个成分。

Figure 1. Component diagram

图1. 组件图

将四个评判指数进行主成分分析后转化为主成分1、2两大类。可以看出第一大类与第二大类总和的累积贡献率达到了73%，说明在信息降维处理之后，信息丢失的很少，基本可以使用降维后的信息代替原来信息。但是由于主成分1、2难以文字解释，于是进行因子旋转，得到两个更加易于解释的主成分(表3、图2)。

Table 3. Component matrix a after rotation

表3. 旋转后的成分矩阵^a

提取方法：主成分分析法。

旋转方法：凯撒正态化最大方差法。

^a旋转在3次迭代后已收敛。

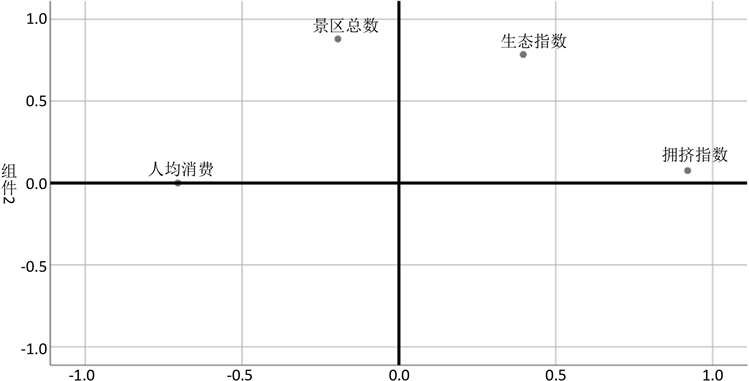
Figure 2. Component diagram after rotation

图2. 旋转后的组件图

由主成分1和主成分2的组件图和成分矩阵得出：1) 主成分1主要与拥挤指数和人均消费成较大相关，主成分2主要由生态指数与景区总数成较大相关。2) 主成分1与拥挤指数成极大正相关，而与人均消费成极大负相关。旅游者旅游时不被拥挤困扰，那么将需要花费更多，将主成分1命名为代价指数。3) 主成分2与景区指数和生态指数均成极大正相关。城市的旅游条件包括景点数目和生态环境越好，主成分2水平越高，将主成分2命名为硬件指数。

代入相关数据得到不同城市关于主成分1、2的散点图(图3)。

Figure 3. Scatter

图3. 散点图

由图可以看出，所有城市较均匀的分布在原点附近，但仍然存在扬州、北京、重庆、深圳这四个特异点的存在。根据对主成分的相关解释可以得出，北京与重庆的硬件指数远高于其他城市的水平，相应的旅游条件优越；深圳的代价指数远高于其他城市，硬件指数比大部分样本城市高；扬州的硬件指数一般，但是相应的代价指数很低。为了散点图得到更好的效果，进行数据筛选，对扬州、北京、重庆、深圳这四个城市变量进行剔除，得到新的不同城市关于主成分1、2的散点图。

Figure 4. Scatter plot after eliminating variation points

图4. 剔除变异点后的散点图

从图4中可以看出，广州、杭州、苏州、上海、成都五个城市位于图像的上方，说明这些城市的硬件指数较高。广州、呼伦贝尔、三亚、丽江、哈尔滨等7个城市在图中偏左边，说明这些城市能够以较高的旅游消费为代价而获得较为宽松、不拥挤的旅游体验，而武汉、合肥等城市去旅游时可能相对花费更少但旅游体验可能会相对较差，可能需要忍耐拥堵的烦恼。

4.2. 聚类分析

对这些不同的城市还进行了聚类分析，分为四类(图5)。

第一类城市以上海、成都、昆明为代表，这些城市的显著特点是硬件水平较高，但旅游时可能会有拥挤的风险。第二类城市以三亚、呼伦贝尔为代表，这些城市可能硬件水平没那么高，但在旅游时的体验可能会较好，不会有拥挤的烦恼。第三类城市以广州、苏州、杭州为代表，这些城市硬件水平较高，且旅游时体验会较好，但花费可能较高。第四类城市以合肥、南昌、贵阳为代表这些城市硬件水平不是很高，而且旅游时可能会承担拥挤的烦恼，但花费较低。

5. 结论

基于SPSS对不同城市进行旅游业发展影响因素的分析，是一种简单可行的方法，可以通过对数据处理来评判旅游发展水平和状况，对旅游业的管理者提供一定的参考意义。从上述分析中，可以得出以

Figure 5. Cluster analysis chart

图5. 聚类分析图

下结论和建议：

1) 在主成分1和主成分2的构建中，主成分1代价指数和主成分2硬件指数比较客观地反映城市旅游的现状，两个主成分是符合实际的。

2) 在对各个城市的描述中，我们所构造的评判指数是行之有效的。在这一条件下提取出的两个主成分(硬件指数、代价指数)对各个城市的描述有良好的区分度和一定的指导意义。通过对城市的评价变量构造和处理，能够在一定范围内进行一定程度上的对比。

3) 发现一些城市如北京、深圳等在旅游的某一指数远高于其他城市，说明此城市在旅游中担当着领头羊的作用，对于旅游发展有重要影响。