在非惯性系下开放环境中的四体纠缠

Tetrapartite Entanglement of an Open Quantum System in Accelerated Frames

摘要: 本文主要研究了四体GHZ量子态在开放环境中非惯性系下的纠缠变化，探究了当三个观察者加速时，系统A和系统AB与环境接触时，纠缠的变化情况。接着探究了当四个观察者加速时，只有系统A与环境接触时，它们的纠缠变化情况。

Abstract: In this paper, we mainly study the entanglement of tetrapartite GHZ quantum states in an open environment in a noninertial system, and explore the entanglement changes when the three observers accelerate, and when the system A and system AB contact with the environment. Then we explore the entanglement changes of four observers when they all accelerate, only when the system A contacts the environment.

1. 引言

在量子计算和量子信息中，纠缠是一个很重要的概念 [1] [2] [3]。近些年来随着对量子信息科学和相对论的进一步研究，人们开始研究在非惯性系下的多体态的物理特征。量子系统的纠缠不可避免的受到外界环境的影响，所以人们研究了二体或者三体量子态在环境下的纠缠变化 [4]，也得到了一些纠缠的变化特征。

本文主要研究了四体GHZ量子态在开放环境中非惯性系下的纠缠变化，探究了当三个观察者加速时，系统A和系统AB与环境接触时，纠缠的变化情况。接着探究了当四个观察者加速时，只有系统A与环境接触时，它们的纠缠变化情况。最后比较了当只有系统A与环境接触时，当有三个观察者和四个观察者时，它们的纠缠变化情况。

2. 基本概念与知识

在非惯性系下，Rindler坐标适合描述一类具有均匀加速的观察者，而另一个保持惯性系的观察者可以用Minkowski坐标描述。我们利用单模近似模型，将Minkowski空间的真空态 $|0\rangle$ 和单粒子态 $|1\rangle$ 转化为Rindler空间的粒子态的张量积的形式，通过变换运算符，可以得到下列运算关系 [5]：

${|0\rangle }_M=\cos r{|0\rangle }_{\mathrm{Ⅰ}}{|0\rangle }_{\mathrm{Ⅱ}}+\sin r{|1\rangle }_{\mathrm{Ⅰ}}{|1\rangle }_{\mathrm{Ⅱ}}$ (1)

${|1\rangle }_M={|1\rangle }_{\mathrm{Ⅰ}}{|0\rangle }_{\mathrm{Ⅱ}}$ (2)

其中 $\cos r={\left({\text{e}}^{-2\pi wc/a}+1\right)}^{-1/2}$，式子中的 $a,r$ 分别代表加速观察者的加速度和加速参数，w代表对应的频率。另一方面加速观察者是在Rindler区域一，与Rindler区域二是不相联系的，对不相关的区域二求迹，可以得到所需要的四体态。

接下来介绍计算纠缠的测量方法。对于一个多体系统 ${\rho }_{\alpha \beta \gamma }$，我们常用的测量是负度 [6]，它的定义如下：

$N_{\alpha \beta }=\Vert {\rho }_{\alpha \beta }^{{{\rm T}}_{\alpha }}\Vert -1$ (3)

$N_{\alpha \left(\beta \gamma \right)}=\Vert {\rho }_{\alpha \beta \gamma }^{{{\rm T}}_{\alpha }}\Vert -1$ (4)

另一方面，对于一个矩阵M， ${\lambda }_i^{(-)}$ 是它的所有负的特征值，有下面的公式：

$\Vert M\Vert -1=2{\displaystyle \sum \left|{\lambda }_i^{(-)}\right|}$

所以等式(3)和(4)可以改写如下形式：

$N_{\alpha \beta }=2{{\displaystyle \sum \left|{\lambda }_{\alpha \beta }^{(-)}\right|}}^i$

$N_{\alpha \left(\beta \gamma \right)}=2{{\displaystyle \sum \left|{\lambda }_{\alpha \left(\beta \gamma \right)}^{(-)}\right|}}^i$

剩余纠缠定义如下 [5]：

${\pi }_{\alpha }=N_{\alpha \left(\beta \gamma \right)}^2-N_{\alpha \beta }^2-N_{\alpha \gamma }^2$

${\pi }_{\beta }=N_{\beta \left(\alpha \gamma \right)}^2-N_{\beta \gamma }^2-N_{\beta \alpha }^2$

${\pi }_{\gamma }=N_{\gamma \left(\alpha \beta \right)}^2-N_{\gamma \alpha }^2-N_{\gamma \beta }^2$

一般 ${\pi }_{\alpha }\ne {\pi }_{\beta }\ne {\pi }_{\gamma }$，于是 $\pi$ -纠缠定义为：

${\pi }_{\alpha \beta \gamma }=\frac{1}{3}\left({\pi }_{\alpha }+{\pi }_{\beta }+{\pi }_{\gamma }\right)$

用类似于上述定义纠缠度的方法，我们可以把定义扩展到四个量子位，定义如下 [7]：

${\pi }_{\alpha }=N_{\alpha \left(\beta \gamma \delta \right)}^2-N_{\alpha \beta }^2-N_{\alpha \gamma }^2-N_{\alpha \delta }^2$

${\pi }_{\beta }=N_{\beta \left(\alpha \gamma \delta \right)}^2-N_{\beta \alpha }^2-N_{\beta \gamma }^2-N_{\beta \delta }^2$

${\pi }_{\gamma }=N_{\gamma \left(\alpha \beta \delta \right)}^2-N_{\gamma \alpha }^2-N_{\gamma \beta }^2-N_{\gamma \delta }^2$

${\pi }_{\delta }=N_{\delta \left(\alpha \beta \gamma \right)}^2-N_{\delta \alpha }^2-N_{\delta \beta }^2-N_{\delta \gamma }^2$

因此我们可以定义总的纠缠：

${\pi }_4=\frac{1}{4}\left({\pi }_{\alpha }+{\pi }_{\beta }+{\pi }_{\gamma }+{\pi }_{\delta }\right)$

由于开放的量子系统总是处在复杂的环境中，本文所涉及的环境是：相位阻尼环境，在这里的子系统分别只与自己的环境相互作用，与其他子系统不相互交流。相位阻尼环境有如下形式：

$E_0^i=\left(\begin{array}{cc}1& 0\\ 0& \sqrt{1-P_i}\end{array}\right),E_1^i=\left(\begin{array}{cc}0& 0\\ 0& \sqrt{P_i}\end{array}\right)$

其中i是从1到N的整数，也表示第i个系统的相位阻尼算符， $p_i$ 是一个与时间有关的参数。另外系统与环境之间的相互作用可以写成下列关系式：

$L\left(\rho \right)={\displaystyle \underset{u\cdots v}{\sum }{E}_u^1}\otimes \cdots \otimes E_v^N\rho E_u^{1{\rm T}}\otimes \cdots \otimes E_v^{N{\rm T}}$ (5)

其中 $\rho$ 是量子系统没有与环境接触就出之前所处的状态， $L\left(\rho \right)$ 是与环境作用后的系统的状态。

3. 四体GHZ态与相位阻尼环境作用只有三个观察者加速

我们将考虑由Alice，Bob，Charlie 和Daniel四个观察者共享的四体GHZ态，定义如下：

$|GHZ\rangle =\frac{1}{\sqrt{2}}\left[|0_A{0}_B{0}_C{0}_D\rangle +|1_A{1}_B{1}_C{1}_D\rangle \right]$

其中GHZ态的下标 $A,B,C,D$ 分别代表四个观察者。当只有Bob，Charlie和Daniel这三个观察者都以相同的加速参数r加速时，我们运用式子(1)和(2)，并通过对区域二分别求偏迹，可以得到下面量子态：

$\begin{array}{c}{\rho }_{A{B}_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}}=\frac{1}{2}[{\cos }^{6}r|0000\rangle \langle 0000|+{\cos }^{4}r{\sin }^{2}r|0001\rangle \langle 0001|\\ +{\cos }^{4}r{\sin }^{2}r|0010\rangle \langle 0010|+{\cos }^{2}r{\sin }^{4}r|0011\rangle \langle 0011|\\ +{\cos }^{4}r{\sin }^{2}r|0100\rangle \langle 0100|+{\cos }^{2}r{\sin }^{4}r|0101\rangle \langle 0101|\\ +{\cos }^{2}r{\sin }^{4}r|0110\rangle \langle 0110|+{\sin }^{6}r|0111\rangle \langle 0111|\\ +{\cos }^{3}r|1111\rangle \langle 0000|+{\cos }^{3}r|0000\rangle \langle 1111|+|1111\rangle \langle 1111|]\end{array}$

接下来量子态 ${\rho }_{A{B}_1{C}_1{D}_1}$ 中只有A系统与相位阻尼环境相接触，运用式子(5)，可以得到与环境作用后的态，再通过分别对四个子系统求部分转置，可以得到下列矩阵：

$\begin{array}{c}{\rho }_{A{B}_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}}^{{{\rm T}}_{B_1}}=\frac{1}{2}[{\cos }^{6}r|0000\rangle \langle 0000|+{\cos }^{4}r{\sin }^{2}r|0001\rangle \langle 0001|\\ +{\cos }^{4}r{\sin }^{2}r|0010\rangle \langle 0010|+{\cos }^{2}r{\sin }^{4}r|0011\rangle \langle 0011|\\ +{\cos }^{4}r{\sin }^{2}r|0100\rangle \langle 0100|+{\cos }^{2}r{\sin }^{4}r|0101\rangle \langle 0101|\\ +{\cos }^{2}r{\sin }^{4}r|0110\rangle \langle 0110|+{\sin }^{6}r|0111\rangle \langle 0111|+|1111\rangle \langle 1111|\\ +\sqrt{1-p}{\cos }^{3}r|0100\rangle \langle 1011|+\sqrt{1-p}{\cos }^{3}r|1011\rangle \langle 0100|]\end{array}$

$\begin{array}{c}{\rho }_{A{B}_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}}^{{{\rm T}}_{C_1}}=\frac{1}{2}[{\cos }^{6}r|0000\rangle \langle 0000|+{\cos }^{4}r{\sin }^{2}r|0001\rangle \langle 0001|\\ +{\cos }^{4}r{\sin }^{2}r|0010\rangle \langle 0010|+{\cos }^{2}r{\sin }^{4}r|0011\rangle \langle 0011|\\ +{\cos }^{4}r{\sin }^{2}r|0100\rangle \langle 0100|+{\cos }^{2}r{\sin }^{4}r|0101\rangle \langle 0101|\\ +{\cos }^{2}r{\sin }^{4}r|0110\rangle \langle 0110|+{\sin }^{6}r|0111\rangle \langle 0111|+|1111\rangle \langle 1111|\\ +\sqrt{1-p}{\cos }^{3}r|0010\rangle \langle 1101|+\sqrt{1-p}{\cos }^{3}r|1101\rangle \langle 0010|]\end{array}$

$\begin{array}{c}{\rho }_{A{B}_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}}^{{{\rm T}}_{D_1}}=\frac{1}{2}[{\cos }^{6}r|0000\rangle \langle 0000|+{\cos }^{4}r{\sin }^{2}r|0001\rangle \langle 0001|\\ +{\cos }^{4}r{\sin }^{2}r|0010\rangle \langle 0010|+{\cos }^{2}r{\sin }^{4}r|0011\rangle \langle 0011|\\ +{\cos }^{4}r{\sin }^{2}r|0100\rangle \langle 0100|+{\cos }^{2}r{\sin }^{4}r|0101\rangle \langle 0101|\\ +{\cos }^{2}r{\sin }^{4}r|0110\rangle \langle 0110|+{\sin }^{6}r|0111\rangle \langle 0111|+|1111\rangle \langle 1111|\\ +\sqrt{1-p}{\cos }^{3}r|0001\rangle \langle 1110|+\sqrt{1-p}{\cos }^{3}r|1110\rangle \langle 0001|]\end{array}$

经过一些计算，我们可以得到：

$\begin{array}{c}{N}_{A\left(B_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}=-2\times (\frac{3}{4}{\cos }^{4}r-\frac{3}{4}{\cos }^{2}r-\frac{1}{4}{\cos }^{6}r+\frac{1}{4}-\frac{1}{4}(15{\cos }^{4}r-6{\cos }^{2}r\\ -{4p{\cos }^{6}r-16{\cos }^{6}r+15{\cos }^{8}r-6{\cos }^{10}r+{\cos }^{12}r+1)}^{\frac{1}{2}})\end{array}$

$N_{B_{\mathrm{Ⅰ}}\left(A{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}=-2\times \left(\frac{1}{4}{\cos }^{4}r-\frac{1}{4}{\cos }^{3}r\times {\left({\cos }^{2}r-4p-2{\cos }^{4}r+{\cos }^{6}r+4\right)}^{\frac{1}{2}}-\frac{1}{4}{\cos }^{6}r\right)$

$N_{C_{\mathrm{Ⅰ}}\left(A{B}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}=-2\times \left(\frac{1}{4}{\cos }^{4}r-\frac{1}{4}{\cos }^{3}r\times {\left({\cos }^{2}r-4p-2{\cos }^{4}r+{\cos }^{6}r+4\right)}^{\frac{1}{2}}-\frac{1}{4}{\cos }^{6}r\right)$

$N_{D_{\mathrm{Ⅰ}}\left(A{B}_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}\right)}=-2\times \left(\frac{1}{4}{\cos }^{4}r-\frac{1}{4}{\cos }^{3}r\times {\left({\cos }^{2}r-4p-2{\cos }^{4}r+{\cos }^{6}r+4\right)}^{\frac{1}{2}}-\frac{1}{4}{\cos }^{6}r\right)$

$N_{ij}=0,i,j=A,B_{\mathrm{Ⅰ}},C_1,D_{\mathrm{Ⅰ}},i\ne j$

${\pi }_4=\frac{1}{4}\left(N_{A\left(B_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}^2+3N_{B_{\mathrm{Ⅰ}}\left(A{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}^2\right),{\prod }_4=\sqrt[4]{N_{A\left(B_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}^2\times N_{B_{\mathrm{Ⅰ}}\left(A{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}^6}$

从下面的图1中我们可以看出，只有系统A与环境接触，对于加速参数r分别取三个特殊值，随着退化参数p增大， ${\pi }_4$ 都是减少的，最后都是减少到0，没有纠缠。对于相同的退化参数p，加速参数r越大，相应的纠缠度就越小。 ${\prod }_4$ 的变化趋势如图2所示，它随着加速参数r和退化参数p也是逐步减少。类似上面的的算法，我们假设系统A和B_I都与相同的相位阻尼环境相接触，通过计算得到：

$\begin{array}{l}{N}_{B_{\mathrm{Ⅰ}}\left(A{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}=N_{C_{\mathrm{Ⅰ}}\left(A{B}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}=N_{D_{\mathrm{Ⅰ}}\left(A{B}_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}\right)}\\ =-2\times \left(\frac{1}{4}{\cos }^{4}r-\frac{1}{4}{\cos }^{6}r-\frac{1}{4}\left({\cos }^{3}r\times {\left({\cos }^{2}r-8p-2{\cos }^{4}r+{\cos }^{6}r+4p^2+4\right)}^{\frac{1}{2}}\right)\right)\end{array}$

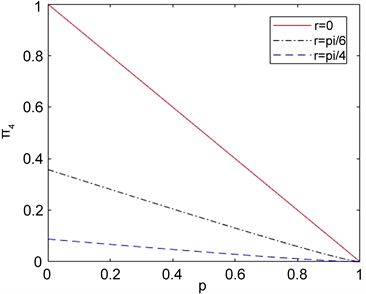
Figure 1. Curve: 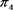as a function of the acceleration p for the phase damping environment

图1. 对于相位阻尼环境，纠缠随退化参数变化的情况

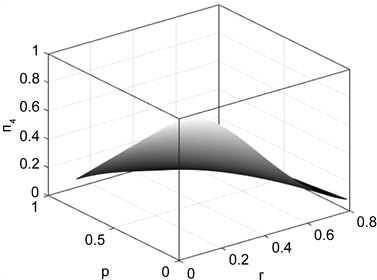
Figure 2. Curve: ${\Pi }_{\text{4}}$ as a function of the acceleration p for the phase damping environment

图2. 对于相位阻尼环境，纠缠随退化参数变化的情况

由于其他的纠缠公式比较复杂，所以没有写出来， ${\pi }_4$ 如图3所示，它也是随着退化参数减少到0，从图中可以看出加速参数最大的， ${\pi }_4$ 最先减少到0。

接下来当 $r=pi/4$，两种情况的 ${\pi }_4$ 的变化情况如图4所示，黑色曲线表示只有系统A与环境接触的情况，蓝色曲线表示系统AB与相同环境接触时的情况，从图中可以看出当 $p=0$，两种情况刚开始纠缠度是一样的，随着p的增大，与环境接触的系统越多，也就是当系统AB都与环境接触，纠缠程度下降的越快，当p接近0.85时， ${\pi }_4$ 减少到0。

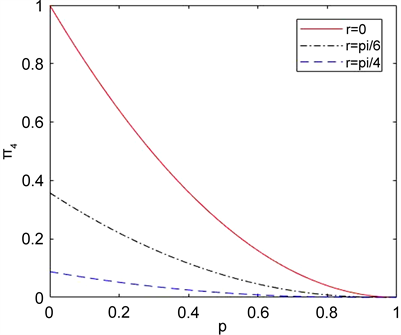
Figure 3. Curve: 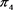as a function of the acceleration p for the phase damping environment

图3. 对于相位阻尼环境，纠缠随退化参数变化的情况

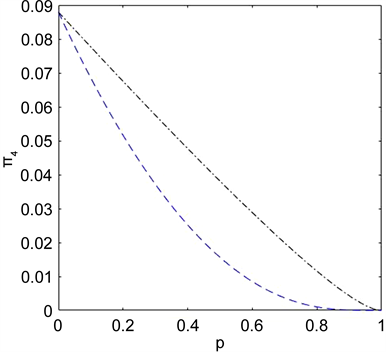
Figure 4. Curve: ${\pi }_4$ as a function of the acceleration p for the phase damping environment

图4. 对于相位阻尼环境，纠缠随退化参数变化的情况

4. 四体GHZ态与相位阻尼环境作用四个观察者都加速

当四个观察者Alice，Bob，Charlie和Daniel都加速时，加速参数分别是 $r_A,r_B,r_C,r_D$，GHZ态变成下列形式：

$\begin{array}{c}{|\Phi \rangle }_A{{}_B}_{CD}=\frac{1}{\sqrt{2}}[\cos r_A\cos r_B\cos r_C\cos r_D|00000000\rangle +\cos r_A\cos r_B\cos r_C\sin r_D|00000011\rangle \\ +\cos r_A\cos r_B\sin r_c\cos r_D|00001100\rangle +\cos r_A\cos r_B\sin r_c\sin r_D|00001111\rangle \\ +\cos r_A\sin r_B\cos r_c\cos r_D|00110000\rangle +\cos r_A\sin r_B\cos r_C\sin r_D|00110011\rangle \\ +\cos r_A\sin r_B\sin r_C\cos r_D|00111100\rangle +\cos r_A\sin r_B\sin r_C\sin r_D|00111111\rangle \end{array}$

$\begin{array}{c}+\sin r_A\cos r_B\cos r_c\cos r_D|11000000\rangle +\sin r_A\cos r_B\cos r_C\sin r_D|11000011\rangle \\ +\sin r_A\cos r_B\sin r_C\cos r_D|11001100\rangle +\sin r_A\cos r_B\sin r_C\sin r_D|11001111\rangle \\ +\sin r_A\sin r_B\cos r_C\cos r_D|11110000\rangle +\sin r_A\sin r_B\cos r_C\sin r_D|11110011\rangle \\ +\sin r_A\sin r_B\sin r_C\cos r_D|11111100\rangle +\sin r_A\sin r_B\sin r_C\sin r_D|11111111\rangle \\ +|10101010\rangle ]\end{array}$

为了方便计算，我们让 $r_A=r_B=r_C=r_D=r$，仅仅只让系统A与相位阻尼环境作用，其他的系统不与环境接触，通过运用等式(5)，再对区域二求偏迹后，得到下列式子：

$\begin{array}{c}{\rho }_{A_{\mathrm{Ⅰ}}{B}_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}}=\frac{1}{2}[{\cos }^{8}r|0000\rangle \langle 0000|+\sqrt{1-p}{\cos }^{4}r|0000\rangle \langle 1111|\\ +{\cos }^{6}r{\sin }^{2}r|0001\rangle \langle 0001|+{\cos }^{6}r{\sin }^{2}r|0010\rangle \langle 0010|\\ +{\cos }^{4}r{\sin }^{4}r|0011\rangle \langle 0011|+{\cos }^{6}r{\sin }^{2}r|0100\rangle \langle 0100|\\ +{\cos }^{4}r{\sin }^{4}r|0101\rangle \langle 0101|+{\cos }^{4}r{\sin }^{4}r|0110\rangle \langle 0110|\\ +{\cos }^{2}r{\sin }^{6}r|0111\rangle \langle 0111|+{\cos }^{6}r{\sin }^{2}r|1000\rangle \langle 1000|\end{array}$

$\begin{array}{l}+{\sin }^{4}r{\cos }^{4}r|1001\rangle \langle 1001|+{\sin }^{4}r{\cos }^{4}r|1010\rangle \langle 1010|\\ +{\sin }^{6}r{\cos }^{2}r|1011\rangle \langle 1011|+{\sin }^{4}r{\cos }^{4}r|1100\rangle \langle 1100|\\ +{\sin }^{6}r{\cos }^{2}r|1101\rangle \langle 1101|+{\sin }^{6}r{\cos }^{2}r|1110\rangle \langle 1110|\\ +\sqrt{1-p}{\cos }^{4}r|1111\rangle \langle 0000|+\left({\sin }^{8}r+1\right)|1111\rangle \langle 1111|]\end{array}$

再通过分别对系统 $A,B,C,D$ 求偏转置，得到它们的矩阵，再通过一些计算可以得到：

$\begin{array}{l}{N}_{A_{\mathrm{Ⅰ}}\left(B_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}=N_{B_{\mathrm{Ⅰ}}\left(A_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}=N_{C_{\mathrm{Ⅰ}}\left(A_{\mathrm{Ⅰ}}{B}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}=N_{D_{\mathrm{Ⅰ}}\left(A_{\mathrm{Ⅰ}}{B}_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}\right)}\\ =-2\times (\frac{1}{4}{\cos }^{2}r-\frac{1}{4}\left(3\times {\cos }^{4}r\right)+{\cos }^{6}r-\frac{1}{2}{\cos }^{8}r-{\cos }^{2}r\times (17\times {\cos }^{4}r\\ -6\times {\cos }^{2}r-4\times p\times {\cos }^{4}r-12\times {\cos }^{6}r+{4\times {\cos }^{8}r+1)}^{\frac{1}{2}}\times \frac{1}{4})\end{array}$

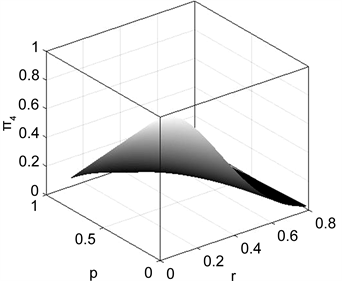
Figure 5. Curve: ${\pi }_4$ as a function of the acceleration p,r for the phase damping environment

图5. 对于相位阻尼环境，纠缠随退化参数变化的情况

Figure 6. Curve: ${\Pi }_4$ asa function of the acceleration p for the phase damping environment

图6. 对于相位阻尼环境，纠缠随退化参数变化的情况

这四个纠缠度量的数都是相等的，所以通过计算发现二体纠缠都为0，也即：

$N_{ij}=0,i,j=A,B_{\mathrm{Ⅰ}},C_1,D_{\mathrm{Ⅰ}},i\ne j$

${\pi }_4={\Pi }_4=N_{A_{\mathrm{Ⅰ}}\left(B_{\mathrm{Ⅰ}}{C}_{\mathrm{Ⅰ}}{D}_{\mathrm{Ⅰ}}\right)}^2$

图形如图5所示，纠缠度随着参数 $p,r$ 逐渐减少到0，纠缠完全被破坏。

对于GHZ态，接下来我们讨论当仅仅只有系统A与环境接触时，有三个观察者加速时和全部都加速时，它们的加速参数都是 $r=pi/6$，纠缠度情况变化如图6所示。从图中可以看到当 $p=0$，只有三个观察者加速时，初始总纠缠度大于0.35，而当全部观察者都加速时，初始总纠缠数接近0.25。随着加速参数的逐渐增大， ${\Pi }_{\text{4}}$ 几乎同时逐渐减少到0。我们可以看出环境对纠缠度的影响是大于加速度的。

NOTES

^*第一作者。