基于最小二乘法的灰色系统应用

Application of Grey System Based on Least Square Method

摘要: 本文主要研究了长沙空气质量与多种影响因素之间的关系，利用各季度AQI的平均值作为空气质量好坏的衡量指标。首先，利用灰色关联分析的方法，对各个影响因素做了定性的分析，计算出各个影响因素对各季度AQI平均值的相对关联度。根据灰色关联分析的结果做优势分析，并得出影响各季度AQI平均值的五个主要影响因素，分别为日均最高温、降水量、绿化面积、日均最低温和大风级天数。然后，根据优势分析的结论，将五个主要影响因素作为自变量，各季度AQI平均值作为因变量，并假设空气质量与主要影响因素的关系为线性关系，做了相应的回归分析。根据所收集的数据，利用最小二乘法给出了各个参数的无偏估计，从而建立了主要影响因素与各季度AQI平均值之间的数学表达式，用于制定空气质量的改善方案。最后，建立了灰色系统下的GM(1,1)模型，并利用最小二乘原理对模型进行了白化求解，然后对2017第四季度的AQI平均值和2018第一季度的AQI平均值进行了预测。并对预测结果进行了残差检验，发现预测效果并不理想，在文章结尾处给出了改进的GM(1,1)模型，并重新对后两个季度的AQI平均值进行预测，预测结果为：2017年第四季度AQI平均值的预测值为67.3718，2018年第一季度AQI平均值的预测值为84.9393，与实际结果差别不大，说明了模型的有效性。

Abstract: This paper mainly studies the relationship between air quality and various influencing factors in Changsha, using the average AQI of each quarter as a measure of air quality. First of all, using the method of grey correlation analysis, the paper makes a qualitative analysis of each influencing factor, and calculates the relative correlation degree of each influencing factor to the average AQI of each quarter. According to the results of the grey correlation analysis, the superiority analysis is made, and five main factors influencing the average AQI of each quarter are obtained, which are the highest daily temperature, precipitation, green area, lowest daily temperature and gale days. Then, according to the conclusion of advantage analysis, five main influencing factors are taken as independent variables, the average AQI of each quarter is taken as dependent variable, and the relationship between air quality and main influencing factors is assumed to be linear, and the corresponding regression analysis is made. According to the collected data, the unbiased estimation of each parameter is given by using the least square method; thus the mathematical expression between the main influencing factors and the average AQI of each quarter is established, which is used to formulate the air quality improvement plan. Finally, the GM (1,1) model under the grey system is established, and the model is whitened by using the least square principle. And the AQI average in the fourth quarter of 2017 and the first quarter of 2018 are predicted. Then the residual test is carried out on the prediction results, and it is found that the prediction effect is not ideal. At the end of the article, an improved GM (1,1) model is given, and the AQI average value of the last two quarters is predicted again. The prediction result is: the AQI average value in the fourth quarter of 2017 is 67.3718, and the AQI average value in the first quarter of 2018 is 84.9393, which is not much different from the actual result, indicating the effectiveness of the model.

1. 问题背景

近年来，空气质量成为了大多数城市关注力度较高的问题，影响空气质量的因素多种多样，本问题研究长沙空气质量与一些影响因素之间的关系，并且预测出之后的两个季度(2017年第四季度至2018年第一季度)中空气质量情况；找出与空气质量关系较为密切的因素，并将这些因素作为自变量做关于空气质量的回归分析。收集的影响因素及数据见表1，空气质量的标准以AQI [1] 为参考量，近年来各季度(从2015年第一季度至2017第三季度)的AQI平均值见图1折线统计图。

根据可能影响空气质量的因素 [2] 和长沙当地情况可认为长沙空气质量主要与人口密度、橘洲烟花的燃放、生产力度的大小、工业影响、农林业影响 [3] 、绿化带的面积、大风、温度、降雨量 [4] 有关。

其中用各季度生产总值来衡量生产力度，认为生产总值越高生产力度越强；用各季度第一产业生产总值 [5] 表示农林业的影响；用各季度第二产业生产总值 [5] 表示工业的影响(认为工业生产总值越多则进行的工业活动越多)；用风级 [6] 大于三级(在这里认为大于三级风属于大风情况 [7] )的天数来表示风力影响；并将气温分为日均最高温 [6] 和日均最低温 [6] 研究其影响；用常住人口的数量来衡量长沙人口密度，且因为常住人口数量无法按季度统计，所以一年的四个季度中均用该年所统计的常住人口数量作为参考值。

Figure 1. AQI quarterly broken line chart in recent years

图1. AQI近年各季度折线统计图(AQI与各子影响因素收集数据见附录)

2. 问题分析

本问题研究长沙空气质量与一些影响因素之间的关系，用长沙各季度的AQI平均值作为长沙空气质量的衡量标准。为了得出各子因素与AQI之间的相对关系，可利用灰色关联分析 [8] 的方法，选取适当的分辨系数ρ，计算得出各因素与AQI之间的相关度，对比各相关度，做优势分析并找出与空气质量关系较为密切的因素，我们可以称这些因素为主要影响因素。为了进一步得出空气质量与主要影响因素之间的具体关系，可以对空气质量和主要影响因素做回归分析，并利用最小二乘法确定出空气质量与主要影响因素之间的具体表达式，并做相应的分析。根据2015年第一季度至2017年第三季度AQI的平均值构建GM(1,1)模型，确定灰微分方程，并利用最小二乘法求出其相应白化方程的参数，然后利用该GM(1,1)模型对2017年第一季度和2018年第二季度的AQI平均值进行预测。

3. 模型建立及解答

3.1. 优势分析

灰色关联分析方法，是根据因素之间发展趋势的相似或相异程度，衡量因素间关联程度的一种方法。我们可以利用该方法粗略的得出长沙空气质量与其影响因素之间的相对关联程度，从而进行优势分析。

3.1.1. 建立参考数列与比较数列

本问题是分析长沙空气质量与其影响因素之间的关系，显然将长沙各季度的AQI平均值作为参考数列，设为 $x_0$ 。

$x_0=\left(x_0\left(1\right),x_0\left(2\right),\cdots ,x_0\left(11\right)\right)=\left(117.0556,68.89011,\cdots ,52.54348\right)$

其中参考数列 $x_0$ 中的各分量分别为2015年第一季度至2017年第三季度各季度AQI的平均值。

同理，比较数列则为可能影响长沙空气质量的十个因素，十个影响因素依次为，常住人口、橘洲烟花燃放次数、生产总值、第一产业、第二产业、绿化面积、风级超过三级天数、日均最高温、日均最低温和降水量，将其设为 $x_i$ 。

$x_i=\left(x_i\left(1\right),x_i\left(2\right),\cdots ,x_i(11))\right)$

其中 $x_i\left(k\right)$ 表示第i个影响因素第k个季度的指标值。

3.1.2. 标准化数据

由于不同的影响因素对空气质量的影响效应是不同的，例如有的影响因素指标与空气质量成正比关系，也有影响因素指标与空气质量成反比关系，所以为了使所有影响因素指标的影响效应相同，需要进行数据标准化，将与空气质量成反比关系的影响因素指标转化为正比关系。

从直观角度可确定橘洲烟花燃放次数业、第二产业与AQI成正相关；绿化面积、风级超过三级天数、日均最高温、日均最低温和降水量与AQI成负相关；而常住人口、生产总值、第一产业不能直接确定正负相关关系，则由公式确定正负相关。

${\sigma }_i={\displaystyle \underset{k=1}{\overset{10}{\sum }}k{x}_i\left(k\right)}-{\displaystyle \underset{k=1}{\overset{10}{\sum }}{x}_i\left(k\right)}{\displaystyle \underset{k=1}{\overset{10}{\sum }}\frac{k}{10}}$

若子因素与 ${\sigma }_0$ 同号则为正相关，反之则为负相关，计算结果见表1。

Table 1. System resulting data of standard experiment

表1. 相关关系计算

所以最终得出各个子因素与母因素AQI的相关性见表2。

Table 2. System operating parameters

表2. 各子因素与母因素AQI的相关性

3.1.3. 求灰色关联系数

所谓的关联程度，实质上是曲线间几何形状的差别程度。因此各曲线间差值大小，可作为关联程度的衡量尺度。对于该灰色关联分析模型，一个参考数列 $x_0$ 有若10个比较数列 $x_i$ ，在分辨系数 $\rho$ 取0.5的前提下，各比较数列与参考数列在各个时刻(即曲线中的各点)的关联系数 ${\zeta }_i\left(k\right)$ 可由下列公式算出：

${\zeta }_i\left(k\right)=\frac{\underset{s}{\min }\underset{t}{\min }\left|x_0\left(t\right)-x_s\left(t\right)\right|+\rho \underset{s}{\max }\underset{t}{\max }\left|x_0\left(t\right)-x_s\left(t\right)\right|}{\left|x_0\left(k\right)-x_i\left(k\right)\right|+\rho \underset{s}{\max }\underset{t}{\max }\left|x_0\left(t\right)-x_s\left(t\right)\right|}$

其表示含义是第i个影响因素对AQI在k时刻的关联系数。

3.1.4. 计算关联度

因为关联系数是比较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值，所以它的数不止一个，而信息过于分散不便于进行整体性比较。因此有必要将各个时刻(即曲线中的各点)的关联系数集中为一个值，即求其平均值，作为比较数列与参考数列间关联程度的数量表示，公式如下：

$r_i=\frac{1}{10}{\displaystyle \underset{k=1}{\overset{10}{\sum }}{\zeta }_i(k)}$

最终计算各个子因素与母因素的相关度见表3。

Table 3. System operating parameters

表3. 各子因素与母因素AQI的相关性

关联度越接近于1，说明关联度越好。从表中可以得出与AQI相关度最高的五个子因素由大到小依次是日均最高温、降水量、绿化面积、日均最低温和大风级天数，则认为这五个子因素为主要影响因素。

将分析结果与实际结合可以得出：

1) 从日均最高温和日均最低温可以看出长沙的空气质量主要受季节的影响，搭配图1可看到春冬季空气质量较差；夏秋季空气质量较好。

2) 从降水量的影响可以看出，降雨过后有利于空气中的细颗粒物沉淀，更易于扩散，所以降水量大的季度空气质量较好。

3) 从绿化面积的影响可以看出，绿色植被可以净化空气，所以长沙市的绿化面积越大空气质量越好。

4) 大风级天数越多，则大颗粒的污染物被吹散的可能性就越大，所以空气质量越好。

以上四点的分析结果均符合客观事实。

除优势因素之外，还可以看出橘洲的烟花燃放次数对AQI的影响最小，从侧面反映出通过减少橘洲烟花燃放次数来改善空气质量的效果并不明显。

3.2. 回归分析

回归分析是比较常用的统计方法，在各种预报预测中，能利用最小二乘原理建立因变量与一组自变量之间的数学关系式，也能定量的分析出各自变量对因变量的影响，为了进一步得出空气质量与主要影响因素之间的具体关系，我们接下来对空气质量和主要影响因素做回归分析。

3.2.1. 建立线性回归模型

首先，我们假设空气质量与主要影响因素的关系为线性关系，则可认为空气质量与主要影响因素的关系表达式为：

$y_{AQI}={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_3{x}_3+{\beta }_4{x}_4+{\beta }_5{x}_5+\epsilon$

其中， $x_1$ 表示自变量绿化面积， $x_2$ 表示自变量大风级天数， $x_3$ 表示自变量日均最高温， $x_4$ 表示自变量日均最低温， $x_5$ 表示自变量降水量， $\epsilon$ 是测量值的误差，我们可以把 $\epsilon$ 看做是数学期望为零的随机变量。奥无疑问，这里的 ${\beta }_0,{\beta }_1,\cdots ,{\beta }_5$ 就是待估计参数，可以根据自变量组和因变量的观测值估计出这些参数，接下来我们要做的就是利用观测值对这些参数进行估计。

3.2.2. 参数估计

为了方便计算，将自变量的观测值记为：

$Y_{AQI}=\left(\begin{array}{c}{y}_{AQI1}\\ ⋮\\ y_{AQIn}\end{array}\right)$

将每次观察下的误差记为：

$\epsilon =\left(\begin{array}{c}{\epsilon }_1\\ ⋮\\ {\epsilon }_n\end{array}\right)$

将自变量组记为：

将待估计参数记为：

$\beta =\left(\begin{array}{c}{\beta }_0\\ ⋮\\ {\beta }_5\end{array}\right)$

则原关系式就可以表示为：

$Y_{AQI}=X\beta +\epsilon$

根据最小二乘原理，尽可能的使每次观察误差的平方和达到最小，我们令：

$Q={\epsilon }^{\prime }\epsilon ={\left(Y_{AQI}-X\beta \right)}^{\prime }\left(Y_{AQI}-X\beta \right)$

为了寻找使得Q达到最小值的参数估计量 $\hat{\beta }$ ，我们可以先利用微积分求出上述方程的驻点，然后再验证其驻点就是最小值点，Q对 ${\beta }_i$ 分别求偏导数得：

$\frac{\partial Q}{\partial {\beta }_i}=-2{\displaystyle \underset{t=1}{\overset{n}{\sum }}\left[y_{AQIt}-{\displaystyle \underset{j=1}{\overset{5}{\sum }}{\beta }_j{x}_{tj}}\right]\cdot x_{ti}},i=0,1,\cdots ,5$

化简得待估计参数 $\beta$ 的估计量 $\hat{\beta }$ ：

$\hat{\beta }={\left(X^{\prime }X\right)}^{-1}{X}^{\prime }y$

因为在该组数据中，通过计算可知 $X^{\prime }X$ 是非奇异矩阵，所以上述估计量成立，利用MATLAB可以求得：

$\hat{\beta }=\left(\begin{array}{c}\begin{array}{c}-7.95\\ 49.12\\ -1.02\end{array}\\ \begin{array}{c}2.95\\ -5.01\\ -0.03\end{array}\end{array}\right)$

具体每个参数 ${\beta }_i$ 的估计值见表4。

Table 4. System operating parameters

表4. 各子因素与AQI的相关性

3.3. 灰色预测

灰色系统理论认为对既含有已知信息又含有非确定信息的系统进行预测，就是对在一定方位内变化的、与时间有关的灰色过程的预测。尽管各季度AQI平均值的变化看似是随机的、杂乱无章的，但毕竟是有序的、有界的，因此这一数据集合具备潜在的规律，灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。灰色系统的预测是基于最小二乘原理的预测，但又与线性回归预测不同，灰色预测可以认为是对一组时间序列进行预测，不需要自变量的观测值，其缺陷是只适用于短期预测。

3.3.1. 数据处理

首先我们要构造原始数列，构造规则与灰色关联法参考数列的规则相同，原始数列的具体情况如下：

$x^{\left(0\right)}=\left(x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),\cdots ,x^{\left(0\right)}\left(11\right)\right)=\left(117.0556,68.89011,\cdots ,52.54348\right)$

为了保证预测的可靠性，需要检验数列的级比是否合理，级比数列计算公式如下：

$\lambda \left(k\right)=\frac{x^{\left(0\right)}\left(k-1\right)}{x^{\left(0\right)}\left(k\right)},k=1,2,\cdots ,11$

所计算的级比数列为：

$\left(1.69,1.05,0.75,0.86,1.68,0.93,0.78,0.86,1.51,1.21)\right)$

级比应落在区间 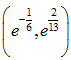，即区间 $\left(0.\text{846481},\text{1}.\text{166311}\right)$ 内才能通过检验，这是建立GM(1,1)模型的一

个必要条件，显然该级比数列不符合，则应对数列 $x^{\left(0\right)}$ 做适当平移，将级比数列中每一分量都加一常数300得：

$y^{\left(0\right)}=x^{\left(0\right)}+\left(300,300,\cdots ,300\right)=\left(317.06,368.89,\cdots ,352.54\right)$

再次检验新数列 $y^{\left(0\right)}$ 的级比是否合理：

${\lambda }_y\left(k\right)=\frac{y^{\left(0\right)}\left(k-1\right)}{y^{\left(0\right)}\left(k\right)},k=1,2,\cdots ,11$

所计算的级比数列为：

$\left(1.13,1.01,0.94,0.96,1.11,0.99,0.95,0.97,1.09,1.03\right)$

显然新数列的级比是符合标准的。

3.3.2. 建立GM(1,1)模型

为了降低数据的波动性和随机性，我们利用 $y^{\left(0\right)}$ 数列做一次累加，累加生成数列记为 $y^{\left(1\right)}$ ，累加生成能使任意非负数列、摆动的与非摆动的，转化为非减的、递增的。

$y^{\left(1\right)}\left(k\right)={\displaystyle {\sum }_{i=1}^k{y}^{\left(0\right)}\left(i\right)},k=1,2,\cdots ,11$

为了建立灰微分方程，我们需要计算加生成数 $y^{\left(1\right)}$ 的均值数列，可根据如下公式进行计算：

$z^{\left(1\right)}\left(k\right)=0.5y^{\left(1\right)}\left(k\right)+0.5y^{\left(1\right)}\left(k-1\right),k=2,3,\cdots ,11$

于是定义GM(1,1)的灰微分方程模型为：

$y^{\left(0\right)}\left(k\right)+a{z}^{\left(1\right)}\left(k\right)=b,k=1,2,\cdots ,11$

其相应的白化微分方程为：

$\frac{\text{d}{y}^{\left(1\right)}}{\text{d}t}+a{y}^{\left(1\right)}\left(t\right)=b$

其中， $y^{\left(0\right)}\left(k\right)$ 称为灰导数，a称为发展系数， $z^{\left(1\right)}\left(k\right)$ 称为白化背景值，b称为灰作用量。

将11个时刻的数据带入方程可得方程组：

$\{\begin{array}{l}{y}^{\left(0\right)}\left(1\right)+a{z}^{\left(1\right)}\left(1\right)=b\\ y^{\left(0\right)}\left(2\right)+a{z}^{\left(1\right)}\left(2\right)=b\\ ⋮\\ y^{\left(0\right)}\left(11\right)+a{z}^{\left(1\right)}\left(11\right)=b\end{array}$

我们可以很明显的看出，求解发展系数a和灰作用量b的值需要采用最小二乘法，这也是本文第二次用到最小二乘法。

记参数向量为：

$u={\left(a,b\right)}^{\text{T}}$

记因变量的观测值向量为：

$Y={\left(y^{\left(0\right)}\left(2\right),y^{\left(0\right)}\left(3\right),\cdots ,y^{\left(0\right)}\left(11\right)\right)}^{\text{T}}$

记自变量组的观察值矩阵为：

$B=\left[\begin{array}{cc}-z^{\left(1\right)}\left(2\right)& 1\\ ⋮& ⋮\\ -z^{\left(1\right)}\left(11\right)& 1\end{array}\right]$

则由最小二乘法的原理可知，我们所求的发展系数a和灰作用量b的值，为误差平方和达到最小时所对应的值，设

$J\left(\hat{u}\right)={\left(Y-B\hat{u}\right)}^{\text{T}}\left(Y-B\hat{u}\right)$

根据本文3.2回归分析中的计算方法，可以求得当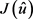达到最小时所对应的 $\hat{u}={\left(a,b\right)}^{\text{T}}$ ，结果见表5。

Table 5. System operating parameters

表5. 发展系数与灰作用量的估计值

3.3.3. 预测

将代入方程求解得发展系数a和灰作用量b的估计值代入方程：

$y^{\left(1\right)}\left(k+1\right)=\left(y^{\left(0\right)}\left(1\right)-\frac{b}{a}\right){\text{e}}^{-ak}+\frac{b}{a},k=1,2,\cdots ,10$

因为在数据处理的过程中，我们将原始数据进行了一次累加，所以需要先将计算所得数据进行还原，即进行累减处理。然后再将还原后的数据各项减去300得到预测值向量 ${\hat{x}}^{\left(0\right)}$ ，预测结果见图2：

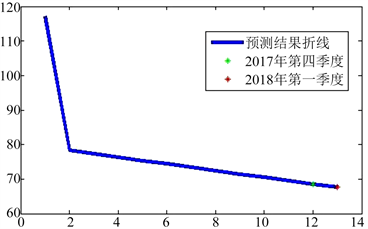
Figure 2. Solution flow based on Greedy Algorithm

图2. 预测结果所示图

综上可得2017年第四季度AQI的平均值为68.60409；2018年第一季度AQI的平均值为67.64813。

由图2可见2017年冬季与2018年春季空气质量相对前几年将有所改善。

为了判断预测效果的好坏，我们需要对预测数据进行残差检验。

令残差为 $\delta \left(k\right)$ ，计算

$\delta \left(k\right)=\left|\frac{x^{\left(0\right)}\left(k\right)-x^{\left(0\right)}\left(k\right)}{x^{\left(0\right)}\left(k\right)}\right|,k=1,2,\cdots ,11$

得残差数列：

$\delta =\left(0,0.14,0.18,0.12,0.25,0.24,0.14,0.13,0.26,0.11,0.32\right)$

可以明显的看出残差值 $\delta \left(4\right)$ ， $\delta \left(5\right)$ ， $\delta \left(8\right)$ 和 $\delta \left(10\right)$ 均大于0.2，所以此次预测的结果准确度较差，预测方案还有待改进，改进后的预测方案将在模型的改进中给出。

4. 模型的改进

4.1. GM(1,1)模型的改进方案

由图1可看出各年四个季度AQI的变化趋势呈现一定的“周期性”，所以为了消除该“周期性”的影响，所以本次建立模型为收集2013至2016各年第四季度AQI的平均值作为参考值预测2017第四季度的AQI平均值；收集2014至2017各年第一季度AQI的平均值作为参考值预测2018第一季度的AQI平均值，原始数据见表6和表7。

假设我们所研究的RGV智能加工流水线的五组参数如表2所示，单位为秒。

Table 6. System operating parameters

表6. 2013至2016各年第四季度AQI的平均值

Table 7. System operating parameters

表7. 2013至2016各年第四季度AQI的平均值

4.2. 改进模型下的预测

由于该模型建立的方法与2.2.2的模型相同，所以以下建立过程进行简写。

设第四季度AQI的平均值的原始数列：

$t^{\left(0\right)}=\left(t^{\left(0\right)}\left(1\right),t^{\left(0\right)}\left(2\right),t^{\left(0\right)}\left(3\right),t^{\left(0\right)}\left(4\right)\right)=\left(152.79,111.78,86.55,82.89\right)$

级比数列为(1.3668,1.2915,1.0441)均落在(0.6703,1.3956)之间，可直接建立GM(1,1)模型。

经过累加、均值处理并建立灰微分方程，可算得预测第四季度AQI的平均值的发展系数 $a_1$ 和灰作用量 $b_1$ ：

$a_1=0.16,b_1=142.18$

代入方程求解得：

$t^{\left(1\right)}\left(k+1\right)=\left(t^{\left(0\right)}\left(1\right)-\frac{b_1}{a_1}\right){\text{e}}^{-ak}+\frac{b_1}{a_1},k=1,2,3,4$

可以算出2017年第四季度AQI平均值的预测值为67.3718。

残差检验数列为：

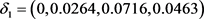
残差数列各值均小于0.1，可认为高度达到预测结果。

设第一季度AQI的平均值的原始数列：

$l^{\left(0\right)}=\left(l^{\left(0\right)}\left(1\right),l^{\left(0\right)}\left(2\right),l^{\left(0\right)}\left(3\right),l^{\left(0\right)}\left(4\right)\right)=\left(131.24,117.06,101.10,95.96\right)$

级比数列为(1.12,1.16,1.0)均落在(0.6703,1.3956)之间，可直接建立GM(1,1)模型。

经过累加、均值处理并建立灰微分方程，可算得预测第一季度AQI的平均值的发展系数 $a_2$ 和灰作用量 $b_2$ ：

$a_2=0.10,b_2=134.95$

代入方程求解得：

$l^{\left(1\right)}\left(k+1\right)=\left(l^{\left(0\right)}\left(1\right)-\frac{b_2}{a_2}\right){\text{e}}^{-ak}+\frac{b_2}{a_2},k=1,2,3,4$

可以算出2018年第一季度AQI平均值的预测值为84.9393。

残差检验数列为：

${\delta }_2=\left(0,0.0133,0.0312,0.0193\right)$

残差数列各值均小于0.1，可认为高度达到预测结果。

综上则预测出较为可靠的后两个季度AQI的平均值，近几年实际的AQI平均值与后两个季度预测的AQI的平均值的变化趋势见图3。

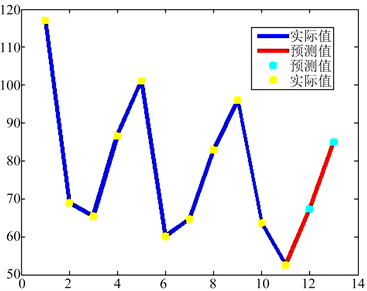
Figure 3. Solution flow based on greedy algorithm

图3. 预测值与实际值

通过图2预测结果与图3预测结果的对比也可以直观的看出，经过改进的GM(1,1)模型预测结果更符合实际，各年四个季度AQI的变化趋势仍然呈现一定的“周期性”。

5. 结论

从优势分析可以看出空气质量的影响主要与季节，降雨量和城市的绿化情况有关，通过控制降雨量和季节改善空气质量是很困难的，但是增大城市绿化面积是可以做到的，通过所收集近年的绿化面积的数据可以看出，近年来长沙市在大力扩增绿化面积，植树造林不仅可以改善我们的生活环境，还会使空气质量大大提高，从问题1.1的结果可以看出，这个决策的效果是非常明显的。自2017年开始，长沙橘洲的烟花燃放次数进行了缩减，目的之一就是为了提高长沙的空气质量，但从所得的结果可以看出，这项决策对于空气质量的影响微乎其微，几乎起不到主体作用。

经过对主要影响因素日均最高温、降水量、绿化面积、日均最低温和大风级天数与各季度AQI平均值的回归分析，可以给出AQI与主要影响因素之间的线性表达式，这对于制定空气质量的改善方案有着非常大的帮助。可以在给定主要影响因素指标的前提下，估算出AQI的平均值，可见，回归分析在环境科学领域有着重要的地位。

针对后两个季度AQI平均值的预测，在第一个建模方案中，虽然该GM(1,1)的部分结果偏差较大，但是从图2可以大致看出AQI值正在逐年递减，空气质量正在逐步的提高，这个结果与长沙市近年所采取提高空气质量的措施是相符的，例如扩增绿化面积，说明近年来采取的一系列提高空气质量的措施起到了一些作用。第二个建模方案较为合理，预测值也更加可信，该方案的预测结果是2017年第四季度AQI平均值的预测值为67.3718，2018年第一季度AQI平均值的预测值为84.9393，与实际结果相差不大，说明了模型的有效性和适用性。

基金项目

湖南省大学生创新创业训练计划项目(No. S201910536031)。

附录

数据