外掠平板湍流边界层对流传热特性解析预测方法

An Analytical Method of Convective Heat Transfer Prediction in an Incompressible Turbulent Boundary Layer on a Flat Plate

摘要: 外掠平板湍流流动特性是研究湍流传热特性的基本问题之一，具有重要的理论意义和工程应用价值。将不可压缩湍流边界层划分为层流底层和湍流核心区，分别采用三次多项式和幂函数代表两个区域的速度场(温度场)分布，利用积分方法建立了动量方程和能量方程组并获得显式解析解，通过四阶龙格–库塔法得到速度和温度边界层厚度分布。与以往模型对比表明，选择1/5次幂函数在湍流核心区符合得较好。以此为基础同时获得了湍流边界层的对流热传递特性。获得的解析解与Blackwell、Moffat和Kays等人的试验结果，以及普朗特–泰勒二层模型和Schlichting经验公式对比表明具有较好的一致性，证明了理论模型的正确性。

Abstract: The study on the steady turbulent flows over a flat plate is one of the basic problems of convective heat transfer processes, which has the key theoretical significance and wide engineering applica-tions. The incompressible turbulent boundary layer is divided into the laminar sublayer and tur-bulent core zone, respectively, for steady turbulent flows over a flat plate, and both of the velocity and temperature profiles in respective zone are characterized by the cubic polynomial or power function. The momentum and energy equation groups are accordingly established by the integral method, and the analytical solutions of the integro-differential equation groups are obtained by carrying out the fourth-order Runge-Kutta method. It is shown that a 1/5 power function has the best agreement with the previous classical models in the turbulent core zone. The convective heat transfer characteristics and profiles on the wall are also obtained for steady turbulent flows. It is indicated that analytical solutions of the present model are in good agreement with the experi-mental measurements by Blackwell, Moffat & Kays, respectively, as well as Prandtl-Taylor’s tur-bulent two-layer theoretical model and Schlichting’s empirical formula, which validates the present theoretical solutions.

1. 引言

湍流边界层广泛应用于航空航天、能源动力和冶金等领域 [1] [2]。外掠平板湍流流动特性是研究湍流速度场、温度场和对流热传递特性的基本问题之一，具有重要的理论研究意义 [3]。湍流边界层形成的物理机制极为复杂，常用的湍流模型包括BL代数模型(零方程模型)、SA一方程模型、k-ω和k-ε等二方程模型，以及雷诺应力模型等 [4] [5]。目前，外掠平板湍流问题研究主要采用数值模拟和试验分析的方法 [6] [7] [8]，理论研究方法的文献相对较少，典型的包括：Rubesin [9] 研究了变壁温不可压缩湍流边界层内对流换热问题，采用1/7幂律描述速度和温度分布，但需以速度边界层厚度作为已知条件。Reynolds [10] 对比了Rubesin等人的求解过程，通过积分分析研究了具有壁面阶梯温度分布的平板传热。Thomas [11] 采用基于表面更新模型的速度和温度分布，获得了均匀壁面处不可压缩湍流边界层的换热特性。崔杰 [12] 根据不可压缩湍流边界层内的Reichardt立方律得到了湍流边界层内速度分布显式表达式。Sucec [13] 考虑了尾迹强度对速度和温度分布的影响，利用积分法研究了零压力和逆压力梯度条件下湍流边界层的对流传热。Khademi [14] [15] 利用积分法研究了湍流边界层流动换热特性。上述研究尽管对复杂的湍流机制进行了合理简化，但是大多数模型仍存在相对复杂、求解困难、部分输入参数需要依靠试验结果等不足。为此，本文将在课题组以往研究基础上 [16]，拟采用积分方法，试图建立一种新的解析模型，它无需以试验结果作为已知输入条件，分别采用三次多项式和1/5次幂函数描述层流底层和湍流核心区的速度/温度分布，利用四阶龙格–库塔法获得湍流速度场和温度场的解析解，以此为基础分析对流换热特性分布规律。

2. 理论模型

2.1. 动量方程、能量方程及其边界条件

图1和图2分别将湍流速度和温度边界层划分为层流底层和湍流核心区，划出一固定控制容积1-4-5-8如图3，其中区域3′-4-5-6′ (3-4-5-6)为速度(温度)边界层中的层流底层，区域2′-3′-6′-7′ (2-3-6-7)为速度(温度)边界层中的湍流核心区，这里l为流体层厚度， $\delta$ ( $\Delta$ )为湍流速度(温度)边界层总厚度， ${\delta }_1$ ( ${\Delta }_1$ )为速度(温度)边界层中层流底层厚度， $u_{\infty }$ 和 $T_{\infty }$ 分别为主流区流速和温度， $u_1$ 和 $T_1$ 、 $u_2$ 和 $T_2$ 分别为层流底层、湍流核心区的流速和温度。理论模型中速度和温度均采用时均值，湍流速度(温度)边界层的总厚度在临界位置处与层流速度(温度)边界层厚度相等，并假设：流体不可压缩且物性参数均为常数，主流区流速 $u_{\infty }$ 和壁面温度 $T_s$ 保持恒定，忽略粘性耗散热，忽略速度和温度在层流底层外缘处的速度差异，不考虑转捩区，设湍流从层流末端开始，取临界雷诺数 [14] [15] [17]，湍流初始处( $x=0$ )速度(温度)边界层中的层流底层厚度 ${\delta }_0$ 极薄，参考Khademi [14] [15] 的零厚度假设，这里认为 ${\delta }_0$ 是一个无限接近于零的正数，理论和数值计算结果表明这种处理对模型预测精度几乎没有影响。

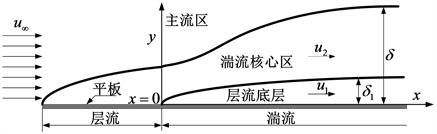
Figure 1. The sketch diagram of velocity boundary layer for turbulent flows on a flat plate

图1. 外掠平板湍流速度边界层示意图

Figure 2. The sketch diagram of thermal boundary layer for turbulent flows on a flat plate

图2. 外掠平板湍流温度边界示意图

Figure 3. Elemental control volume for integral analysis of turbulent boundary layer

图3. 外掠平板湍流控制容积

采用与外掠平板层流边界层完全类似的积分方法 [18] [19]，分别得到动量方程和能量方程如下：

$\{\begin{array}{l}\rho \frac{\text{d}}{\text{d}x}{\displaystyle {\int }_0^{{\delta }_1}{u}_1\left(u_1-u_L\right)\text{d}y}+\rho \frac{\text{d}{u}_L}{\text{d}x}{\displaystyle {\int }_0^{{\delta }_1}{u}_1}\text{d}y+\mu {\frac{\partial u_1}{\partial y}|}_{y=0}-\mu {\frac{\partial u_1}{\partial y}|}_{y={\delta }_1}=0\left(层流底层\right)\\ \rho \frac{\text{d}}{\text{d}x}{\displaystyle {\int }_{{\delta }_1}^{\delta }{u}_2\left(u_2-u_{\infty }\right)\text{d}y}+\rho \frac{\text{d}}{\text{d}x}{\displaystyle {\int }_0^{{\delta }_1}{u}_1}\left(u_L-u_{\infty }\right)\text{d}y-\rho \frac{\text{d}{u}_L}{\text{d}x}{\displaystyle {\int }_0^{{\delta }_1}{u}_1}\text{d}y+\mu {\frac{\partial u_1}{\partial y}|}_{y={\delta }_1}=0\left(湍流核心区\right)\end{array}$ (1)

$\{\begin{array}{l}\rho c_p\frac{\text{d}}{\text{d}x}{\displaystyle {\int }_0^{{\Delta }_1}{u}_{\text{1}}\left(T_1-T_L\right)\text{d}y}+\rho c_p\frac{\text{d}{T}_L}{\text{d}x}{\displaystyle {\int }_0^{{\Delta }_1}{u}_1\text{d}y}+\lambda {\frac{\partial T_1}{\partial y}|}_{y=0}-\lambda {\frac{\partial T_1}{\partial y}|}_{y={\Delta }_1}=0\left(层流底层\right)\\ \rho c_p\frac{\text{d}}{\text{d}x}{\displaystyle {\int }_{{\Delta }_1}^{\Delta }{u}_2\left(T_2-T_{\infty }\right)\text{d}y}+\rho c_p\frac{\text{d}}{\text{d}x}{\displaystyle {\int }_0^{{\Delta }_1}{u}_1\left(T_L-T_{\infty }\right)\text{d}y}-\rho c_p\frac{\text{d}{T}_L}{\text{d}x}{\displaystyle {\int }_0^{{\Delta }_1}{u}_1\text{d}y}+\lambda {\frac{\partial T_1}{\partial y}|}_{y={\Delta }_1}=0\left(湍流核心区\right)\end{array}$ (2)

式中 $u_L$ 和 $T_L$ 分别是速度和温度边界层中层流底层外缘处的速度和温度， $\rho$ 、 $\mu$ 、 $c_p$ 、 $\lambda$ 分别为流体的密度、动力粘度、定压比热容和导热系数。考虑到多数情况下流体普朗特数 $Pr<1$，故设 ${\delta }_1<{\Delta }_1$，在控制容积 $\text{d}x$ 范围内 ${\delta }_1$ 、 ${\Delta }_1$ 沿x保持不变。

动量和能量方程应当满足如下边界条件：

${u_1|}_{y=0}={\frac{{\partial }^2{u}_1}{\partial y^2}|}_{y=0}=0$， ${u_1|}_{y={\delta }_1}={u_2|}_{y={\delta }_1}=u_L$， ${u_2|}_{y=\delta }=u_{\infty }$， $\mu {\frac{\partial u_1}{\partial y}|}_{y={\delta }_1}=\left(\mu +{\mu }_t\right){\frac{\partial u_2}{\partial y}|}_{y={\delta }_1}$， ${T_1|}_{y=0}=T_s$， ${\frac{{\partial }^2{T}_1}{\partial y^2}|}_{y=0}=0$，， ${T_1|}_{y={\Delta }_1}={T_2|}_{y={\Delta }_1}=T_L$， ${T_2|}_{y=\Delta }=T_{\infty }$。这里 ${\mu }_t$ 为湍流动力粘度； $a_t$ 为湍流热扩散率；根据普朗特混合长度理论， ${\mu }_t=\rho l^2\left|\frac{\partial u_2}{\partial y}\right|$， $l=0.41y$， $a_t=\frac{{\mu }_t}{\rho P{r}_t}$，取湍流普朗特数 $P{r}_t=0.82$ [18]。

2.2. 速度和温度分布函数

认为外掠平板湍流边界层沿x具有相似的速度和温度分布，分别采用三次多项式和幂函数描述层流底层和湍流核心区速度和温度分布：

$\{\begin{array}{l}{u}_1=a_1+a_{2}y+a_3{y}^2+a_4{y}^3\left(0\le y<{\delta }_1\right)\\ u_2=a_5{y}^{1/n}\left({\delta }_1\le y\le \delta \right)\end{array}$ (3a)

$\{\begin{array}{l}\frac{{\theta }_1}{{\theta }_{\infty }}=b_1+b_{2}y+b_3{y}^{\text{2}}+b_4{y}^3\left(0\le y<{\Delta }_1\right)\\ \frac{{\theta }_{\text{2}}}{{\theta }_{\infty }}=b_5{y}^{1/n}\left({\Delta }_1\le y<\Delta \right)\end{array}$ (4a)

式中 ${\theta }_1=T_1-T_s$， ${\theta }_{\text{2}}=T_{\text{2}}-T_s$， ${\theta }_{\infty }=T_{\infty }-T_s$。当 $n=5$ 时，可得速度和温度分布函数的各系数：

$a_1=a_3=b_1=b_3=0$， $a_2=u_{\infty }\left(\frac{7}{5}-\frac{{\mu }_t}{10\mu }\right){\delta }_1^{-4/5}{\delta }^{-1/5}$， $a_4=u_{\infty }\left(-\frac{2}{5}+\frac{{\mu }_t}{10\mu }\right){\delta }_1^{-14/5}{\delta }^{-1/5}$， $a_5=u_{\infty }{\delta }^{-1/5}$， $b_5={\Delta }^{-1/5}$，， $b_4=\left(-\frac{2}{\text{5}}+\frac{\rho c_p{a}_t}{10\lambda }\right){\Delta }_1^{-14/5}{\Delta }^{-1/5}$。

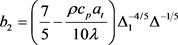代入式(3a)、(4a)，即得外掠平板湍流边界层的速度和温度的显式表达式如下：

$\{\begin{array}{l}\frac{u_1}{u_{\infty }}=\frac{1}{10}{\left(\frac{{\delta }_1}{\delta }\right)}^{1/5}\left[\left(14-\frac{{\mu }_t}{\mu }\right)\frac{y}{{\delta }_1}-\left(4-\frac{{\mu }_t}{\mu }\right){\left(\frac{y}{{\delta }_1}\right)}^3\right]\left(0\le y<{\delta }_1\right)\\ \frac{u_2}{u_{\infty }}={\left(\frac{y}{\delta }\right)}^{1/5}\left({\delta }_1\le y\le \delta \right)\end{array}$ (3b)

$\{\begin{array}{l}\frac{{\theta }_1}{{\theta }_{\infty }}=\frac{1}{10}{\left(\frac{{\Delta }_1}{\Delta }\right)}^{1/5}\left[\left(\text{14}-\frac{\rho c_p{a}_t}{\lambda }\right)\frac{y}{{\Delta }_1}-\left(4-\frac{\rho c_p{a}_t}{\lambda }\right){\left(\frac{y}{{\Delta }_1}\right)}^3\right]\left(0\le y<{\Delta }_1\right)\\ \frac{{\theta }_{\text{2}}}{{\theta }_{\infty }}={\left(\frac{y}{\Delta }\right)}^{1/5}\left({\Delta }_1\le y<\Delta \right)\end{array}$ (4b)

2.3. 数学求解

将速度和温度分布式(3)和(4)代入动量和能量积分方程组(1)和(2)的相应部分，整理成下述四个微分方程

$\frac{\text{d}{\delta }_{\text{1}}}{\text{d}x}=f_{\text{1}}\left({\delta }_1,\delta \right)$ 、 $\frac{\text{d}\delta }{\text{d}x}=f_2\left({\delta }_1,\delta \right)$ 、 $\frac{\text{d}{\Delta }_{\text{1}}}{\text{d}x}=f_{t\text{1}}\left({\delta }_1,\delta ,{\Delta }_1,\Delta \right)$ 和 $\frac{\text{d}\Delta }{\text{d}x}=f_{t2}\left({\delta }_1,\delta ,{\Delta }_1,\Delta \right)$ 的形式，采用四阶龙格

–库塔法在MATLAB软件中求解，得到 ${\delta }_1$ 、 $\delta$ 、 ${\Delta }_1$ 和 $\Delta$ 数值后分别代入速度和温度分布函数(3)和(4)，即得到速度场和温度场的理论分布。

3. 结果讨论

3.1. 速度场

为便于比较，将本文速度解析解转换成无量纲形式 $u^{+}=u/u_{\tau }$，并令 $y^{+}=y{u}_{\tau }/\nu$，其中 $u_{\tau }=\sqrt{{\tau }_s/\rho }$， ${\tau }_s/\rho =\nu a_2$，这里 $\nu$ 、 ${\tau }_s$ 分别为运动粘度和壁面处剪应力。针对湍流核心区速度分布函数分别取幂指数 $n=4,5,6,7$，并与普朗特–泰勒二层模型 [20]、卡门三层模型 [20]、1/7幂律 [21] 进行对比，如图4，发现当 $n=5$ 时，在 $y^{+}\le 100$ 范围内本文速度解析解在层流底层( $y^{+}\le 10.9$ )与普朗特–泰勒二层模型、卡门三层模型几乎完全重合，而在湍流核心区( $y^{+}\ge 10.9$ )与普朗特–泰勒二层模型、卡门三层模型和1/7幂律符合得较为满意，尤其与二层模型最接近，这是由于本文将边界层也划分为两个区域的缘故。为准确计，以下分析中幂函数的指数项均取为1/5。

Figure 4. Comparison of present velocity analytical solutions with previous theoretical models

图4. 本文速度解析解与以往理论模型对比

本文速度解析解与Blackwell [18] 试验结果(其中IDENT 91871为Kays专著 [18] 中的试验数据编号)比较如图5，发现在层流底层和湍流核心区两者均符合得较好，最大相对误差为6.5%。

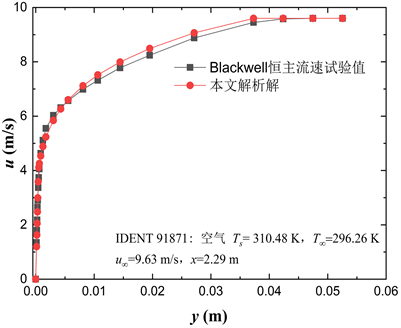
Figure 5. Comparison of present velocity analytical solutions with that of Blackwell’s experimental results

图5. 本文速度解析解与Blackwell试验结果的比较

3.2. 温度场

图6是本文温度解析解与Blackwell [18] 试验结果的对比情况。如图可见，无论在层流底层还是湍流核心区二者均符合得很好，最大相对误差为0.2%。

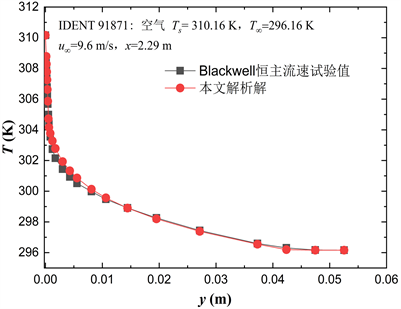
Figure 6. Comparison of present thermal analytical solutions with that of Blackwell’s experimental results

图6. 本文温度解析解与Blackwell试验结果对比

将本文温度解析解转换成无量纲形式 $T^{+}=\frac{\left(T_s-T\right)\sqrt{{\tau }_s/\rho }}{q/\rho c_p}$，其中 $q=-\rho c_p\left(a+a_t\right)\frac{\text{d}T}{\text{d}y}$，a为热扩散率。

图7是本文温度解析解与普朗特–泰勒二层模型 [19] 在 $y^{+}\le 100$ 范围内的对比表明，在层流底层( $y^{+}\le 13.1$ )和湍流核心区( $y^{+}\ge 13.1$ )本文解析解与普朗特–泰勒二层模型均符合得较好，最大相对误差为6.0%。

Figure 7. Comparison of present temperature analytical solutions with Prandtl-Taylor two-layer model

图7. 本文温度解析解与普朗特–泰勒二层模型对比

3.3. 对流热传递特性分析

由努塞尔数的定义可知： $Nu=hx/\lambda =b_{2}x$，这里h是对流换热系数。Schlichting提出的拟合公式 [20] 为 $Nu=0.0296R{e}^{4/5}P{r}^{1/3}$，本文解析解与拟合公式的对比情况如图8，它在 $5\times {10}^5<Re<{10}^7$ 范围内与试验结果符合得较好，二者相对误差不超过2.5%。

Figure 8. Comparison of Nusselt numbers from present model and Schlichting’s fitting formula

图8. 本文解析解获得的努塞尔数与拟合公式对比

本文解析解获得的斯坦顿数 $St=\frac{h}{\rho u_{\infty }{c}_p}=\frac{\lambda b_2}{\rho u_{\infty }{c}_p}=\frac{a{b}_2}{u_{\infty }}$，其中h为对流换热系数。本文斯坦顿数解与

Blackwell [18]、Moffat和Kays [22] 的试验结果均符合得很好，最大相对误差分别为1.4%、2.9%，如图9(a)和图9(b)。

Figure 9. (a) Comparison of Stanton numbers obtained from the present model and Blackwell’s experimental results; (b) Comparison of Stanton numbers from present solution and Moffat and Kays’ experimental results

图9. (a) 本文斯坦顿数解与Blackwell试验结果对比；(b) 本文斯坦顿数解与Moffat和Kays试验结果对比

4. 结果讨论

1) 针对外掠平板不可压缩湍流边界层对流传热问题，将湍流速度(温度)边界层划分为层流底层和湍流核心区，分别采用三次多项式和幂函数代表两个子区域的速度和温度分布，利用积分方法建立了动量方程和能量方程，通过四阶龙格–库塔法获得了速度和温度解析解，并以此为基础获得了湍流边界层的对流热传递特性分布。

2) 经过与以往经典模型比较，发现当幂函数的指数项取1/5时近似效果最佳。本文获得的速度解析解与Blackwell试验结果相比最大相对误差为6.5%，与1/7幂律、普朗特–泰勒二层模型、卡门三层模型符合得较好。温度解析解与Blackwell试验、普朗特–泰勒二层模型结果最大误差为0.2%和6.0%。获得的Nu数与Schlichting经验解误差不超过2.5%。获得的St数分别与Blackwell试验、Moffat和Kays试验的结果相比表明，最大相对误差分别为1.4%和2.9%。以上诸多对比证明了建立的速度、温度和对流热传递解析模型预测结果的正确性和可信性。

3) 提出的理论模型与以往模型相比，形式简单，易于计算，收敛速度快，计算成本低，便于应用；同时也为后续气膜冷却、发汗冷却等边界层理论的深入研究奠定了理论基础。

NOTES

^*通讯作者。