大型建筑紧急疏散的动态优化模型及应用

Dynamic Optimization Model and Application of Large-Scale Building Emergency Evacuation

摘要: 本文针对大型建筑的紧急疏散问题，首先将建筑划分为多个区域，所有区域设为一个状态集合，区域人数设为状态值，区域间人员的转移数量设为状态转移量，构建出一个大型建筑的状态网络。然后，以疏散时间为决策变量，建立基于状态网络理论的动态优化模型。并在获得各区域的拥堵程度和潜在拥堵点的基础上，使用调度因子生成最优的疏散策略。最后，通过实例模拟验证了模型的可行性和疏散策略的高效性。

Abstract: Aiming at the problem of emergency evacuation of large buildings, this paper first divides the building into several areas, all of which are set as a state set, the number of people in the area is set as a state value, and the number of people transferred between areas is set as a state transfer quantity, so as to construct a state network of large buildings. Then, with the evacuation time as the decision variable, a dynamic optimization model based on state network theory is established. After obtaining the congestion level and potential congestion points in each area, the scheduling factor is used to generate the optimal evacuation strategy. Finally, the feasibility of the model and the efficiency of the evacuation strategy are verified by a case simulation.

1. 引言

大型建筑通常都是当地的地标建筑，人群聚集场所。在火灾等突发状况下，由于建筑结构上的复杂性和建筑规模的庞大性，其人员快速疏散策略显得尤为重要，也得到了大型建筑设计者和管理者的广泛关注。早在20世纪30年代，人员疏散研究已经在美国初步兴起，主要用于火灾科学领域。20世纪50~60年代，前苏联Predtechenski，Milinski等人 [1] 进行了大量观测统计工作，归纳出人员疏散流动的基本规律。日本学者Togawa [2] 对密集人群的疏散行为、移动速度进行研究，推导出疏散时间近似公式。加拿大Pauls [3] 等人总结出一系列关于多层建筑疏散时间的经验公式，认为疏散速度与通道宽度呈非线性关系。我国在这一领域的研究主要集中于计算机模拟仿真，具有代表性的工作包括高层建筑人员疏散仿真模型Building Evac [4]、基于元胞自动机的人群疏散模型 [5]、以及基于几何方法的疏散仿真模型GAEvac [6] 等。

以上研究大多没有考虑到人员疏散的动态性，且在疏散过程中过于强调人为引导，给疏散工作带来难度。本文在充分考虑人员疏散的动态性的基础上，提出一种动态模型，将大型建筑抽象为状态网络 [7]，建立关于疏散人数变化的动态方程组，寻找潜在会发生拥堵的地点，再对这些点进行调度建立新的方程组，开发出紧急疏散下的动态优化 [8] 模型，最大化降低疏散工作难度，提高紧急疏散的效率。

2. 使基于状态网络理论的动态优化模型

大型建筑通常人员众多且出口有限，在紧急疏散时，很可能造成局部堵塞，会严重影响疏散的速度和安全 [9]。因此，进行疏散规划首先应找出建筑的潜在拥堵点，再对潜在拥堵点进行疏散优化，进而提高疏散效率。

2.1. 潜在拥堵点

为了寻找潜在拥堵点，首先将建筑的每一层都划分为多个区域，划分规则为：对于含有楼梯的区域，应保证通往下一层的楼梯数量尽可能相等；由于大型建筑内部构造往往是多样化的，为了便于计算，划分区域时应尽量保证各区域面积相近。然后将每一个区域抽象为一个状态空间，构成状态集，状态值为该区域的人数，将楼梯抽象为状态通路。通过观察人员紧急疏散时的本能反应 [10]，在没有人为干预疏散时，由疏散人员根据自己的主观判断进行疏散，通常有以下两种情形：

情形一：区域内有通往下一层的楼梯。

Figure 1. State network diagram of non-intervention evacuation situation 1

图1. 无干预疏散情形一的状态网络图

如图1所示，该区域的人员往往会优先选择通过楼梯疏散。建立状态网络进行描述，可得下列动态方程组：

$X_2\left(k\right)=X_2\left(k-1\right)-f_2\left(k\right)$ (1)

$X_1\left(k\right)=X_1\left(k-1\right)-f_1\left(k\right)+f_2\left(k\right)$ (2)

其中， $X_2\left(k\right)$ 为k时刻状态2的人数，即状态值， $X_2\left(k-1\right)$ 为 $k-1$ 时刻状态2的状态值， $X_1\left(k\right)$ 、 $X_1\left(k-1\right)$ 同理； $f_2\left(k\right)$ 为状态2至状态1的状态转移量， $f_1\left(k\right)$ 同理。

情形二：区域内无楼梯或出口。

Figure 2. State network diagram of non-intervention evacuation situation 2

图2. 无干预疏散情形二的状态网络图

如图2所示，人员会向相邻的区域转移，转移人数通常与区域间人数差值有关，为了量化状态转移量，引入一个选择因子q作不同方向转移人数占总转移人数的权重，计算q值采用如下算法：

$q_j=\{\begin{array}{l}0,X_j\left(k\right)\ge X_i\left(k\right)\\ \frac{X_j\left(k\right)-X_i\left(k\right)}{{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left[X_j\left(k\right)-X_i\left(k\right)\right]}},X_j\left(k\right)<X_i\left(k\right)\end{array}$ (3)

其中， $X_i\left(k\right)$ 为k时刻没有楼梯口的区域i的人数， $X_j\left(k\right)$ 为k时刻相邻区域j的人数，n为相邻区域中满足 $X_j\left(k\right)<X_i\left(k\right)$ 的区域个数。

将图2所示的转移过程用状态网络图描述，可得下列动态方程：

$X_0\left(k\right)=X_0\left(k-1\right)-q_1\cdot h_0\left(k\right)-q_2\cdot h_0\left(k\right)$ (4)

其中， $X_0\left(k\right)$ 为k时刻状态0的状态值， $q_1$ 为状态0转移至状态1的选择因子， $q_2$ 为状态0至状态2的选择因子， $h_0\left(k\right)$ 为k时刻状态0的总状态转移量。

对于所有的状态点，当 $X\left(k\right)>X\left(k-1\right)$ 时，便将该状态视为潜在拥堵点。

2.2. 状态转移量的计算

1) 人流密度

人流密度反映一个空间内人员稠密程度 [11]，其值的计算为：

$D=\frac{N\cdot f}{W\cdot L}\left({\text{m}}^{\text{2}}/{\text{m}}^{\text{2}}\right)$ (5)

其中，N (个)为人流中人员的个数，f (m²)为平均每个人的水平投影面积，W (m)为人流宽度，L (m)为人流长度。由于各区域面积相等，W·L可以视为一个不变的常量。

2) 疏散速度

根据参考文献 [12] 可知，不同地点的疏散速度也是不同的：

紧急情况下，水平通道的平均疏散速度 [13] 为：

$V=\left(1.49-0.36D\right)\times \left(112D^4-380D^3+434D^2-217D+57\right)\left(\text{m}/\text{min}\right)$ (6)

其中D为人流密度，且 $0<D\le 0.92$。

紧急情况下，经过门的平均疏散速度 [13] 为：

$V_0=V\left[1.17+0.13\sin \left(6.03D-0.12\right)\right]\left(\text{m}/\text{min}\right)$ (7)

紧急情况下，下楼梯的平均疏散速度 [13] 为：

$V_1=\frac{1.21V\cdot \left[0.775+0.44e-0.39D\cdot \sin \left(5.16D-0.224\right)\right]}{1.49-0.36D}\left(\text{m}/\text{min}\right)$ (8)

3) 状态转移量

某时刻的状态转移量是该时刻的速度与人流宽度的乘积除以单人平均面积，因此，某时刻水平通道的状态转移量、楼梯的状态转移量和经过门的状态转移量分别定义为：

$h\left(k\right)=\frac{V\left(k\right)\cdot W}{f}$ (9)

$f\left(k\right)=\frac{V_0\left(k\right)\cdot W}{f}$ (10)

$g\left(k\right)=\frac{V_1\left(k\right)\cdot W}{f}$ (11)

2.3. 调度因子

上述疏散方案所建立的状态网络中，含有楼梯口的状态点只能在各楼层间单向转移，与同一楼层内的状态点是不相通的。因此，尝试对潜在拥堵点中含有楼梯口的状态点进行适当调度 [14]，如图3所示，引入一个调度因子d，将0状态值与相邻状态值比较，与选择因子同理求出调度因子的值，即可得到向各相邻状态的转移量，建立动态方程组，然后比较调度前后的总疏散时间的大小，从而决定是否调度。这样能够有效缩短疏散时间，提高疏散效率和安全性。

Figure 3. State network diagram under the action of scheduling factors

图3. 调度因子作用下的状态网络图

图中， $X_0\left(k\right)$ 为潜在拥堵点；m为相邻状态点中满足 $X_0\left(k\right)>X_j\left(k\right)$ 的个数； $X_m\left(k\right)$ 为与0状态相邻的第m个状态； $d_m$ 为0状态至m状态的调度因子，其计算方法为：

$d_m=\{\begin{array}{l}0,X_m\left(k\right)\ge X_0\left(k\right)\\ \frac{X_m\left(k\right)-X_0\left(k\right)}{{\displaystyle \underset{j=1}{\overset{m}{\sum }}\left[X_j\left(k\right)-X_0\left(k\right)\right]}},X_m\left(k\right)<X_0\left(k\right)\end{array}$ (12)

对于0状态可建立如下动态方程：

$X_0\left(k\right)=X_0\left(k-1\right)-{\displaystyle \underset{j=1}{\overset{m}{\sum }}{d}_j{h}_0\left(k\right)}$ (13)

最后建立整栋建筑所有状态的动态方程，计算不同调度点和数量下，最后一个被清空的状态所耗时间，该时间即为总疏散时间，且该时间越小，表明该疏散方案越优。

3. 模型实例

以卢浮宫 [15] 为例，使用模型进行紧急疏散仿真。为了便于求解，假设各个展区人数相等且均匀分布，将卢浮宫的出口等效为三个位于0层的小出口和一个位于−1层的大出口。然后对卢浮宫的−1层至2层进行等面积区域划分，构成状态集，按照模型中寻找潜在拥堵点的规则，初步规划疏散路线，构成边集，如图4所示。

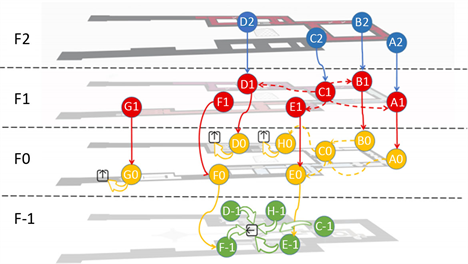
Figure 4. Schematic diagram of the Louvre’s state network

图4. 卢浮宫状态网络示意图

然后对状态集建立动态方程组，以第1层为例，建立的动态方程组如下：

$\{\begin{array}{l}{X}_{A1}\left(k\right)=X_{A1}\left(k-1\right)+f_{A2}\left(k\right)-f_{A1}\left(k\right)+q_{A1}{h}_{C1}\left(k\right)\\ X_{B1}\left(k\right)=X_{B1}\left(k-1\right)+f_{B2}\left(k\right)-f_{B1}\left(k\right)+q_{B1}{h}_{C1}\left(k\right)\\ X_{C1}\left(k\right)=X_{C1}\left(k-1\right)+f_{C2}\left(k\right)-h_{C1}\left(k\right)\\ X_{D1}\left(k\right)=X_{D1}\left(k-1\right)+f_{D2}\left(k\right)-f_{D1}\left(k\right)+q_{D1}{h}_{C1}\left(k\right)\\ X_{E1}\left(k\right)=X_{E1}\left(k-1\right)-f_{E1}\left(k\right)+q_{E1}{h}_{C1}\left(k\right)\\ X_{F1}\left(k\right)=X_{F1}\left(k-1\right)-f_{F1}\left(k\right)\\ X_{G1}\left(k\right)=X_{G1}\left(k-1\right)-f_{G1}\left(k\right)\end{array}$ (14)

式中，A1至G1分别代表第1层的7个状态； $X\left(k\right)$ 为k时刻的状态值； $f\left(k\right)$ 为k时刻通过楼梯的状态转移量； $h\left(k\right)$ 为k时刻通过水平通道的状态转移量；q为选择因子；其他楼层同理。

假设每个状态的初始值为50人，即 $X\left(0\right)=50$，使用Matlab软件对动态方程组进行编程仿真，得到各楼层各状态值变化曲线，以−1层为例，结果如图5所示。

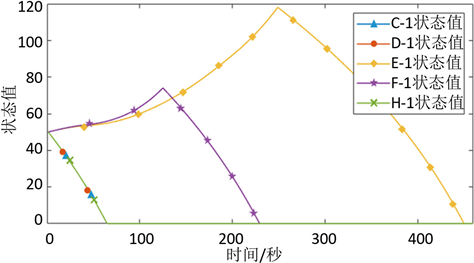
Figure 5. Partial state value change curve (−1 layer)

图5. 部分状态值变化曲线(以−1层为例)

观察各楼层状态值变化曲线，找出状态值变化曲线中含有增加阶段的状态有B0、D0、E0、F0、E − 1、F − 1，即为潜在拥堵点，然后可以结合实际情形，对这些状态进行适当调度。这里以对E0状态进行调度为例，使用模型中的调度因子进行调度，建立E0状态新的动态方程：

$X_{E0}\left(k\right)=X_{E0}\left(k-1\right)+f_{E1}\left(k\right)-f_{E0}\left(k\right)-d_{F0}{h}_{E0}\left(k\right)$ (15)

式中， $X_{E0}\left(k\right)$ 为k时刻E0的状态值， $f_{E1}\left(k\right)$ 为k时刻由E1至E0的状态转移量， $f_{E0}\left(k\right)$ 为k时刻由E1至E − 1的状态转移量， $h_{E0}\left(k\right)$ 为E0水平通道的状态转移量， $d_{F0}$ 为E0至F0的调度因子，考虑人流方向不冲突，所以E0不应往C0或A0调度。

更新动态方程组并使用Matlab模拟仿真，能够发现拥堵程度大幅降低，且疏散时间也有所减小，如图6所示。

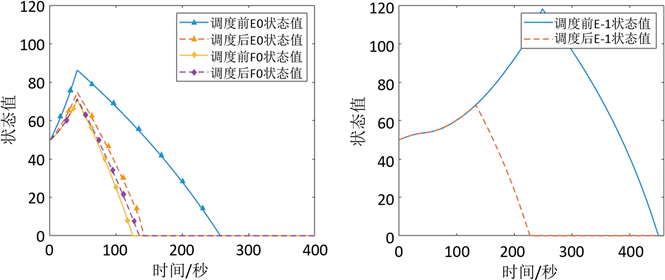
Figure 6. Comparison curve before and after partial state scheduling

图6. 部分状态调度前后对比曲线

从图6中可以看出：调度后E0状态的拥堵程度有所降低，且疏散时间大幅减小，但也牺牲了相邻F0状态的疏散时间，而E − 1状态调度后拥堵程度和疏散时间都有大幅降低。

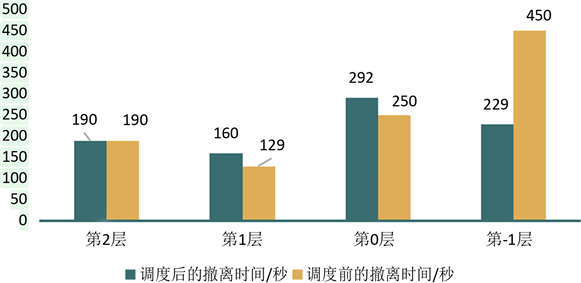
Figure 7. Evacuation time of each floor

图7. 各楼层疏散时间

通过模拟仿真可得调度前后各楼层清空的时间(秒)，如图7所示，从图中可以看出：调度后有效减少了−1层的疏散时间，整栋建筑的疏散时间从450秒降到292秒，可见实施调度的可行性和必要性。

4. 结论

紧急疏散的动态规划模型考虑到疏散过程的动态性，代入建筑的相关参数，即可通过模型求解出建筑各处的拥堵程度及预测疏散状况，并且能反映人员疏散的行为，更形象、更真实地反映疏散过程。

紧急疏散的动态规划模型的独特之处在于：可以得到建筑的潜在拥堵点，在进行疏散规划时，只需要对潜在拥堵点进行适当调度，就能减小疏散管理规划的工作难度，同时也能提高疏散效率，另外还可以对潜在拥堵点所在的位置进行通道改造，具有一定的现实意义。

紧急疏散的动态规划模型从人流群体的角度进行分析，对人员间的差异性考虑不够完善，需要进一步的研究和完善。