1. 引言
铁路工务维修小车旨在解决铁路工作人员沿线施工、维修、抢险时的交通问题,在此基础上增加钢轨曲线防侧磨涂油、线路巡检等项目。其中,安全完成人员、检修及施工设备的运送是工电维修小车的第一要务。探伤小车目前已成功运用于现场测试(如图1所示),对于小车的安全性不容忽视。文献 [1] 对双轨探伤小车下底盘的承载结构的四种不同的型材截面进行有限元分析,通过有限元分析数据比对,确定选取最优的型材截面,提高下底盘承载结构的安全系数。文献 [2] [3] 通过对探伤小车的实际运行测试,对该动力系统理论计算进行试验验证,证实了该计算方法的合理性,确定小车的安全运行。维修小车的研发需要考虑其在不同线路上的动态适应性。铁路线路条件往往复杂多变,除了线路走向的变化,线路上还存在着明显的轨道几何不平顺,这是引起车辆振动的主要因素,小车通过以上线路及不平顺时是否存在脱轨系数、轮重减载率等安全性指标超限问题,是否会发生运动失稳现象,是否满足设备运载需求,这些问题均可通过动力学仿真技术进行动态性能评估,从而得到解答 [4]。
为了研究工务维修小车的安全性,保证运行小车以及作业人员的安全工作,本文基于UM建立了小车多体动力学仿真模型,分析了小车的运动稳定性,确保在正常运行速度范围内,小车不会发生失稳现象,并且通过分析小车在R350 m曲线轨道上惰行、驱动以及制动条件下的轮轨走行状态,并通过统计最大值的轮轴横向力、脱轨系数和轮重减载率等指标来判断其安全性。
2. 工务维修小车结构概述
该车设计速度20 km/h。可运载6人,最大载荷800 kg,在小车的标准配置中,该车整备重量为150 kg,轴重50 kg。工务小车具有新式轮轴式电机,其功率可达750 W,既突出了轻便的特点,又为小车提供了足够的动力。同时,经过调研,走行线路的最小平面曲线半径为350 m。表1给出了小车的相关参数。

Table 1. Relevant parameters of works trolley
表1. 工务小车相关参数
图2给出了工务小车的三维几何模型,可以看出小车的特点是采用四轮承载,各轮均可独立回转,因要求具备装载货物的功能,因此增设了拖斗整车通过六轮承载,同样各车轮均可独立旋转。小车的驱动电机为轮毂式,同步控制,置于前端两个车轮的内部。制动装置置于前轮内部,同样采用同步制动技术。

Figure 2. 3D geometry model of works maintenance dolly
图2. 工务维修小车三维几何模型
3. 动力学分析模型
该车辆是一个并不复杂的机械系统,但各部件之间的相互作用关系相对复杂,为了能够有效的反映主要因素对研究对象的影响,在建模前有必要对小车系统进行简化处理,处理方法如下:
1) 把影响相近及连接紧密的座椅、构架等不影响动力学性能的等效为一个刚体,这些结构件刚度较大,不易产生变形,在建模时仅关注其质量、质心、转动惯量等参数而不考虑结构弹性;
2) 由于小车没有一系悬挂,车体建成刚体与支撑架弹性连接;
3) 车轮的外部是特殊材料,仿真时需要与刚体区分开考虑。
3.1. 基于UM的工务维修小车动力学建模
基于UM动力学仿真软件,根据车辆结构特点,采用自下而上的建模方法,每个刚性部件可简化为一个刚体,通过Joint定义部件的运动自由度,以模拟实际车辆中部件相对于轨道或其它部件的运动形式,在此基础上,通过力元来模拟车辆中的弹簧、阻尼、摩擦等减振元件特性 [5],如图3所示。
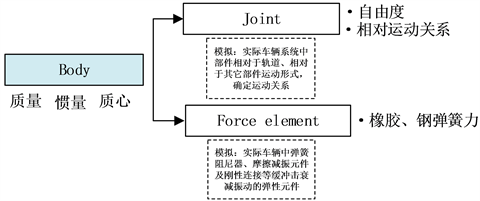
Figure 3. UM multi-body dynamics modeling basic method
图3. UM多体动力学建模基本方法
对于该工务车而言,先建立单个轮对模型,然后通过复制得到整车模型。图4给出了各部件拓扑关系,首先通过自带的轮对模块,输入实际车辆轮对的参数建立两个轮对子系统,其次建立两个1自由度支撑板,随后建立6自由度的车架,支撑板与车架通过铰接的方式赋予一个点头自由度,之后支撑板与车架之间采用可以模拟具有线性和非线性特性的柔性铰Bushing力元建立连接。
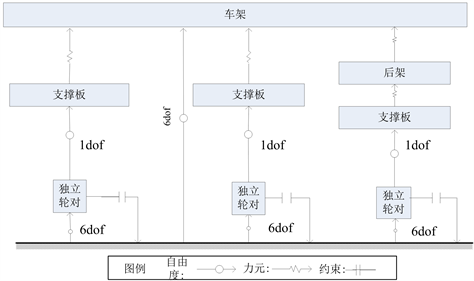
Figure 4. Schematic diagram of topological relation of works dolly model
图4. 工务小车模型拓扑关系示意图
图5为Bushing力元的坐标系定义及数学模型,其中A、B点分别为两个Body上的坐标系基准点,假设两刚体之间的连接距离很近,当B点相对于A点产生相对位移
和转角
时,线性Bushing力元产生的力及力矩 [6]。
(1)
其中
和
为相对移动速度和相对角速度,C和D为B点相对与A点的刚度矩阵和阻尼矩阵。
用Bushing力元来模拟支撑板和车架之间的一系刚度和阻尼的原因有两点,一是:支撑板和车架之间的垂向力可用近似线性的刚度和阻尼代替;二是:Bushing力元还可以通过定义数据点来模拟力和力矩与相对位移和转角之间的函数对应关系,可以用来定义支撑板和车架之间的纵向和横向止挡关系 [7]。

Figure 5. Bushing coordinate system of force elements
图5. Bushing力元的坐标系
3.2. 动力学模型的建立
根据车辆结构和UM坐标系建模原则把小车分为车体和轮对两个部分,轮对部分又可以进一步分为支撑板、独立轮对、驱动装置、制动装置等结构。车体部分分为底盘以及座椅构架。
将各部件三维部件作为刚体导入仿真软件后,遵循体、铰、力元的规则,建立车辆的动力学模型。刚体之间用等效力元模拟部件的连接。刚体座椅构架通过两个位于刚体前后的等效力元与刚体支撑板连接,起到完全固定的作用;独立轮对与支撑板的连接则用了释放Y轴转动的等效力元。小车的主要建模参数如表2所示,小车动力学模型如图6所示。

Table 2. Main parameters of vehicle dynamics model
表2. 车辆动力学模型主要参数

Figure 6. Dynamics model of works maintenance dolly
图6. 工务维修小车动力学模型
小车车轮采用聚氨酯材质,至于聚氨酯车轮与钢轨的接触力学关系,通过设置轮轨接触弹性模量和泊松比,来模拟实际的橡胶轮与钢轨的接触力学特性,法向力的求解基于经典的Hertz理论,而切向力的求解采用Fastsim算法,这与传统机车车辆的动力学求解是一致的。
3.3. 线路不平顺
轨道不平顺功率谱能够真实的反应线路轨道的不平顺状态,无论是评估线路的质量,还是模拟铁路车辆在线路上运行可靠性,都是不可缺少的 [8]。我国铁道科学研究院通过对铁路干线大量测试得到了代表三大重载提速干线的轨道谱,计算方法如公式(2):
(2)
式中,f为空间频率(1/m);A~G为特征系数。
为保证仿真计算条件更加接近真实运行状态,选用上述三大干线轨道谱作为轨道激励,UM拟合曲线图分别如图7所示。
4. 运动稳定性分析与评估
运动稳定性是保障对车辆安全运行的重要性能,对于轮轨式车辆,其重要的考核指标就是确定车辆的非线性临界速度。传统铁道机车车辆确定临界速度的方法是:在轨道上施加一段运用线路轨道谱,使整个系统的振动被激发,然后使车辆系统在平直无不平顺的轨道上运行,当系统的响应不再衰减到平衡位置而是趋于稳定的极限环时,则此时的速度即为车辆临界速度 [9]。本文涉及的工务维修小车采用独立旋转车轮,理论上纵向蠕滑力为零,不会产生蛇行运动,其对中功能主要依靠自身的重力刚度,但实际受力状态是仍然存在横向和自旋蠕滑力,同时存在较小的纵向蠕滑力,因此较高速度条件下仍然可能导致运动失稳。
图8给出了小车在波长10 mm、幅值10 mm的正弦波激扰下车轮横向运动动态响应。从图中可以看出,当车辆速度为37 km/h时,其波形出现振荡后衰减,故此速度下运动呈收敛状态;而为38 km/h时,波形持续振荡,故此速度下发散。所以小车非线性临界速度是37 km/h。
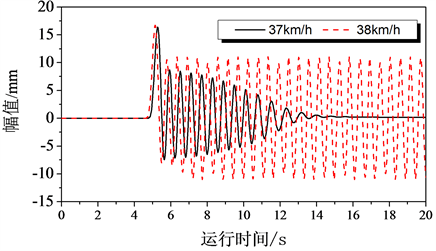
Figure 8. Time history diagram of lateral movement of wheel
图8. 车轮横向运动时间历程图
这样,通过改变速度观察系统响应特征,便可直观确定出小车系统的非线性临界速度为37km/h;能够满足时速20 km/h的运用需求。
5. 工务小车安全性分析
5.1. 计算工况以及安全指标的确定
为了研究小车的运行安全性,使小车在三大干线不平顺等因素的激扰下通过曲线段,设置惰行、驱动、制动的不同计算工况。驱动和制动力以力矩的形式施加到车轮上如图9所示,在一定施加内增至稳定值,同时为了保证车辆能匀速运行,需在车体质心位置施加一反向的运行阻力。对于制动工况,载荷施加方向与此相反。输出不同工况的脱轨系数、轮重减载率以及轮轴横向力特性响应,选取恒定速度一位轮对的时程响应和不同速度的最大值与下表3的安全性评价指标作对比,分析小车的安全性。
根据我国《铁道车辆动力学性能评定和试验鉴定规范》(GB5599-85)、(TB/T 2360-1993)《铁道机车动力学性能试验鉴定方法及评定标准》,选定脱轨系数、轮重减载率及轮轴横向力作为安全性的评价指标,车辆各项动力学性能指标限定值如表3所示。其中,当车轮大幅度减载时,轮轨垂向力和横向力较小,由于测量误差的影响,很难求出正确的脱轨系数,故轮重减载率可以作为辅助评价指标综合评定车辆运行安全性 [10],而轮轴横向力与小车轴重相关。

Figure 9. Application of driving torque and operating resistance
图9. 驱动力矩及运行阻力施加方案

Table 3. Vehicle dynamics performance index perform standard
表3. 车辆动力学性能指标执行标准
5.2. 曲线运行安全性分析
选取典型的小半径曲线进行动力学分析,曲线工况设置为:曲线半径350 m,缓和曲线长度70 m,超高120 mm,圆曲线长度120 m,通过速度20 km/h。通过动力学仿真,得到小车不同计算工况下一位轮对的脱轨系数、轮重减载率、轮轴横向力时程响应,分别如下图10~12所示,通过与动力学性能指标对比分析小车的安全性。对结果分析可知,小车的各类指标在进入前缓和曲线时迅速增大,在曲线段保持较大值,且存在较明显的波动,这是由于进入曲线后小车受离心力的作用使小车轮轨动态相互作用更为剧烈。通过对轮轴横向力的分析可知,驱动、制动工况下的动力学响应波动范围略大于惰行工况计算结果。三种工况的轮重减载率区别不大,这是由于驱动及制动力主要改变了轮轨切向力,对垂向力影响较小,而轮重减载率与轮轨垂向力相关。
5.3. 不同速度下小车曲线运行安全性分析
为了研究工务维修小车以不同速度通过曲线时的安全性,选取5 km/h、10 km/h、15 km/h、20 km/h的速度区间,对模型一位轮对的动力学指标最大值进行统计,并与安全性指标进行对比分析小车的动态安全性。
图13给出了脱轨系数随运行速度的变化规律,可以看出,脱轨系数随速度的增加呈逐渐增大的趋势,特别是在惰行工况下,此外,驱动、制动的脱轨系数最大值相对比较接近,三种工况下,脱轨系数最大值为0.54,与上述安全指标对比可知,在安全范围内。
图14给出了不同运行操纵条件下的轮重减载率最大值随速度的变化规律,对结果分析可以看出,轮重减载率随速度变化的规律同样呈增大的趋势,特别是惰行工况下小车以20 km/h速度运行时,统计最大值为0.59,十分接近第二限度,依据传统机车车辆的评定规范,轮重减载率的第一限度是危险限度,第二限度是允许限度,超过第一限度可能就会出现脱轨,而超过第二限度也会造成危险。为了安全考虑轮重减载率应尽量低于第二限度的允许限度范围内。因此小车在正常运行速度范围内该指标仍然符合规范要求,但由于车辆重量较轻,减载安全性的裕量不大,达到第二限度时就可能会出现脱轨,所以应该保证小车的轮重减载率在第二限度内,不宜进一步提速。

Figure 13. One wheelset Statistic graph of maximum derailment coefficient
图13. 一位轮对脱轨系数最大值统计图

Figure 14. One wheelset Statistical chart of maximum wheel weight loss rate
图14. 一位轮对轮重减载率最大值统计图
图15反映了轮轴横向力最大值随速度的变化趋势,速度越高,轮轨横向动力作用越剧烈,因此轮轴横向力也就越大,当达到20 km/h时,轮轴横向力最大值183 N,与上述安全指标对比,低于209 N的限值,在安全范围内。事实上,过大的轮对与轨道间的横向力将导致轨距加宽、轨排横移或钢轨翻转,增加线路的维修量,甚至危及行车安全,轮轴横向力是为了考评车辆对线路的横向动力作用。但从计算结果可以看出,该小车由于重量低,轮轴横向力要远低于传统意义上机车车辆的数值,因此对线路的影响是微弱的。

Figure 15. One wheelset Statistical chart of maximum transverse force of wheel and axle
图15. 一位轮对轮轴横向力最大值统计图
总的来看,无论是工务维修小车以惰行、驱动还是制动工况运行,在0~20 km/h速度范围内,各动力学指标都在安全限值以内,但由于小车重量轻,轮轨激扰极易引起垂向减载性能恶化,在20 km/h速度运行时,轮重减载率已接近第二限度,不宜进一步提速。
6. 结论
本文以工务维修小车为研究对象,建立了小车的动力学仿真分析模型,讨论了小车的运动稳定性,并分析了典型小半径曲线条件下不同工况小车的动态运行安全性,最后通过统计出不同速度的最大值与安全指标作对比,分析小车的运行安全性。主要结论如下:
1) 工务维修小车的临界速度为37 km/h,所以在运行20 km/h的情况下,不会出现失稳的现象,能够符合实际作业的运行需求。
2) 小车在惰行、驱动和制动条件下通过350 m半径曲线线路时,脱轨系数、轮重减载率和轮轴横向力都是随速度的增加呈增大的趋势,并且在20 km/h时达到最大值,与安全指标作对比,都在安全范围内,但值得注意的是,由于小车重量轻,轮轨激扰极易引起垂向减载性能恶化,在20 km/h速度运行时,轮重减载率已接近第二限度,不宜进一步提速。