一类五次非线性系统的全局动力学

Global Dynamics of a Class of Quintic Nonlinear System

摘要: 本文主要运用微分方程定性理论讨论了一类五次非线性系统的全局动力学行为，该系统在Stringer壳的非线性振动和船舶横摇运动中有着广泛的应用。

Abstract: In this paper, the global dynamic behavior of a class of quintic nonlinear systems is discussed by using the qualitative theory of differential equations. The system is widely used in nonlinear vibration of stringer shell and ship rolling motion.

1. 引言

本文主要讨论下面一类二阶五次微分方程的全局动力学行为：

$x^{″}\left(1+a{x}^2\right)+G\left(x^{\prime }\right)+F\left(x\right)=0$, (1)

其中 $G\left(x^{\prime }\right)=b{x}^{\prime }+ax{x^{\prime }}^2+b{x^{\prime }}^3$ 表示系统的阻尼项 [1] [2] [3]，对于实际系统中不同的材料特性，常数参数a和b会取不同的值， $G\left(x^{\prime }\right)$ 具有不同的表达形式； $F\left(x\right)=x-1.9x^3+0.722x^5$ 表示系统的恢复力矩 [1] [4]。

系统(1)在不同的参数条件下可以转化为多种在工程中有着广泛应用的实际模型。例如，当 $a>0$， $b=0$ 时，系统(1)简化为结构正交异性的Stringer壳结构系统 [4] - [10]，在飞机、航天器和船舶的结构设计中起着不可或缺的作用。对于一般的Stringer壳结构系统，Bayat等人分别通过延拓的哈密顿方法 [7] 和同伦摄动方法 [8] 提供了Stringer壳结构系统做非线性自由振动时的近似解析解。在 $a>0$ 的情况下，Lai等人根据不同的材料参数建立了一个基于谐波平衡法的低阶解析近似解，该半解析解与精确解吻合的非常好 [9]。Liu等人基于结构正交异性的Stringer壳系统，分析了系统坐标中心处的平衡态的稳定性及其近似解析周期解，并通过数值模拟对其进行了验证 [6]。当 $a=0$， $b=0.2$ 时，系统(1)则简化为一类单自由度的船舶横摇模型 [1] [2] [3] [11] [12] [13] [14]。Kreider通过不变流形和Melnikov方法研究了参数强迫、单自由度方程模型对船侧倾的影响 [2]。由于非线性粘滞阻尼和刚度的软化特性，船舶横摇运动表现出复杂的动力学特性。Falzarano等人运用随机动力学理论中的“力矩方程法”和“路径积分法”研究了不规则海洋中横摇响应的概率特性 [11]。Belenky和Weems从大振幅运动程序的数值模拟结果中研究了横摇角和横摇率的独立性 [12]。刘利琴基于非线性随机动力学理论分别研究了随机和规则波浪中，有(无)甲板上浪时船舶横摇的非线性动力学特性 [13]。Zhou和Chen采用解析和数值方法，研究了船舶在规则纵波中参数激励横摇中的混沌运动 [14]。

综上所述，现有文献主要研究了系统(1)在 $a>0$ 时的局部动力学行为；本文将主要探讨系统(1)在 $a<0$ 时的全局动力学行为，但是为了保持系统(1)在不同参数下全局动力学的完整性，我们也将对 $a\ge 0$ 时系统(1)的全局动力学做简要的探讨。

2. 全局动力学

本节我们主要运用微分方程定性理论讨论不同的情形下系统(1)的全局动力学行为。

2.1. 当 $a>0,b=0$ 时的情形

当 $a>0,b=0$ 时，系统(1)是一类具有三势阱的非自然保守系统，文献 [9] [10] 对其局部动力学行为及其半解析的近似解已进行了较为深入的研究，为了直观展现其全局动力学行为，我们绘制了 $a=1,b=0$ 时系统(1)的全局动力学，如图1所示。

2.2. 当 $a=0,b=0.2$ 时的情形

当 $a=0$ 时，系统(1)对应船舶的横摇运动，Nayfeh在其经典著作 [1] 中对 $b=0.2$ 时的情形做了较为详细的介绍，我们不再赘述，但绘制了如图2以展示 $a=0,b=0.2$ 时系统(1)的全局动力学行为。

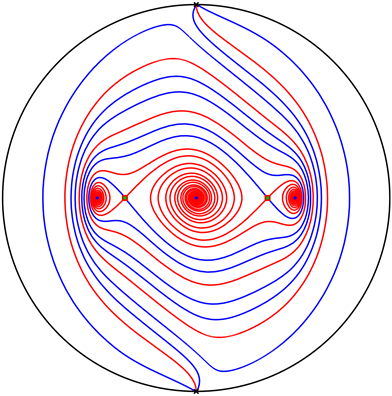
Figure 1. Global phase portraits of system (1) for $a=1,b=0$

图1. 系统(1)在 $a=1,b=0$ 时的全局相图

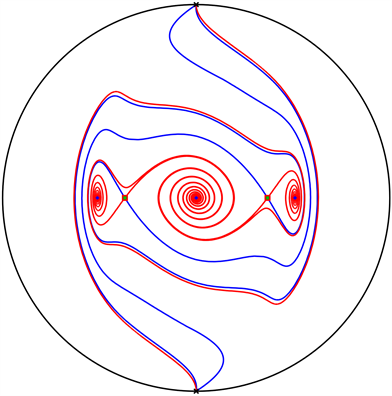
Figure 2. Global phase portraits of system (1) for $a=0,b=0.2$

图2. 系统(1)在 $a=0,b=0.2$ 时的全局相图

2.3. 当 $a=-3,b=0.2$ 时的情形

当 $a<0$ 时，系统(1)的动力学行为极其复杂，我们通过大量的数值模拟发现系统(1)存在11个平衡点，但其定性的性质未发生明显的变化。于是简便起见，本节中我们主要考虑 $a=-3,b=0.2$ 且不考虑临界线 $x^2=-1/a$ 时的情形，则系统(1)可转化为下面的微分方程组系统：

$\begin{array}{l}{x}^{\prime }=y\left(1-3x^2\right),\\ y^{\prime }=-\left(x-1.9x^3+0.722x^5\right)+3x{y}^2-0.2y-0.2y^3.\end{array}$ (2)

易见系统(2)具有11个有限远平衡点：

$e_1=\left(-1.37994,0\right);$

$e_2=\left(-0.852848,0\right);$

$e_3=\left(0,0\right);$

$e_4=\left(0.852848,0\right);$

$e_5=\left(1.37994,0\right);$

$e_6=\left(-0.57735,-8.5252\right);$

$e_8=\left(-0.57735,-0.462344\right);$

$e_9=\left(0.57735,0.462344\right);$

$e_{10}=\left(-0.57735,0.327295\right);$

$e_{11}=\left(0.57735,-0.327295\right).$

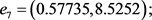
其对应的Jacobi矩阵的特征值分别为：

${\lambda }_{1,1}=-4.00648,{\lambda }_{1,2}=3.80648;$

${\lambda }_{2,1}=-0.1+1.20461i,{\lambda }_{2,2}=-0.1-1.20461i;$

${\lambda }_{3,1}=-0.1+0.994987i,{\lambda }_{3,2}=-0.1-0.994987i;$

${\lambda }_{4,1}=-0.1+1.20461i,{\lambda }_{4,2}=-0.1-1.20461i;$

${\lambda }_{5,1}=-4.00648,{\lambda }_{5,2}=3.80648;$

${\lambda }_{6,1}=-29.5322,{\lambda }_{6,2}=-14.2753;$

${\lambda }_{7,1}=-29.5322,{\lambda }_{7,2}=-14.2753;$

${\lambda }_{8,1}=-1.60161,{\lambda }_{8,2}=1.27335;$

${\lambda }_{9,1}=-1.60161,{\lambda }_{9,2}=1.27335;$

${\lambda }_{10,1}=-1.39806,{\lambda }_{10,2}=1.13378;$

${\lambda }_{11,1}=-1.39806,{\lambda }_{11,2}=\mathrm{1.13378.}$

根据常微分方程的奇点理论可以判断 $e_1$ 、 $e_5$ 、 $e_8$ 、 $e_9$ 、 $e_{10}$ 和 $e_{11}$ 的特征值乘积小于零，故这6个平衡点为鞍点； $e_2$ 、 $e_3$ 和 $e_4$ 的特征值为复数且实部均小于零，故这3个平衡点为稳定焦点， $e_6$ 和 $e_7$ 的特征值均未负实数，故这2个平衡点为稳定结点。

为了探索系统(2)的全局动力学，我们下面继续考虑无穷远平衡点，在 $U_1$ 上作Poincaré变换 $x=1/v,y=u/v$，这将有助于我们实现如何在局部区域 $U_1$ 上绘制系统(2)的矢量场，并可以显示趋于或来自无穷远的轨道，此时系统(2)等价于

$\begin{array}{l}{u}^{\prime }=-0.722+\left(1.9+\left(6-0.2u\right)u^2\right)v^2+\left(-1+\left(-0.2-u\right)u\right)v^4,\\ v^{\prime }=-u{v}^3\left(-3+v^2\right).\end{array}$ (3)

其平衡点为：

$S_1=\left(-0.566891,-1.73205\right),S_2=\left(0.800803,-1.73205\right);$

$S_3=\left(14.7661,-1.73205\right),S_4=\left(0,-1.17254\right);$

$S_5=\left(0,-0.72467\right),S_6=\left(0,0.72467\right);$

$S_7=\left(0,1.17254\right),S_8=\left(-0.566891,1.73205\right);$

$S_9=\left(0.800803,1.73205\right),S_{10}=\left(14.7661,1.73205\right).$

鉴于上述平衡点 $S_1,S_2,\cdots ,S_{10}$ 均不在 $v=0$ 上，所以 $U_1$ 中无平衡点。

同理，我们在 $U_2$ 上作Poincaré变换 $x=u/v,y=1/v$，那么系统(2)等价于

$\begin{array}{l}{u}^{\prime }=0.722u^6-1.9u\left(-0.0333216+u\right)\left(3.15901+u\left(0.0333216+u\right)\right)v^2+\left(1+u\left(0.2+u\right)\right)v^4,\\ v^{\prime }=0.722u^{5}v+0.2v^3-1.9u^3{v}^3+0.2v^5+u{v}^3\left(-3+v^2\right).\end{array}$ (4)

很明显系统(4)右端的项均为高次多项式，故此时 $U_2$ 上 $\left(0,0\right)$ 原点为非初等奇点。

综合上述分析，我们将系统(2)的全局相图绘制如图3所示。

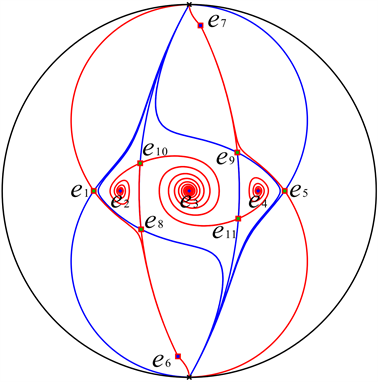
Figure 3. Global phase portraits of system (2) for $a=-3,b=0.2$

图3. 系统(2)在 $a=-3,b=0.2$ 时的全局相图

2.4. 当 $a=-1,b=0.2$ 时的情形

当 $a=-1$ 时，虽然我们用同样的方法可以分析系统(2)亦存在11个有限远平衡点，但其中有4个平衡点是复数，因此我们将此种情况也一并列举出来，其余7个有限远平衡点绘制在其全局相图上的情形如图4所示。除此之外，系统(2)在其他 $a<0$ 时的定性性质未见明显的变化。

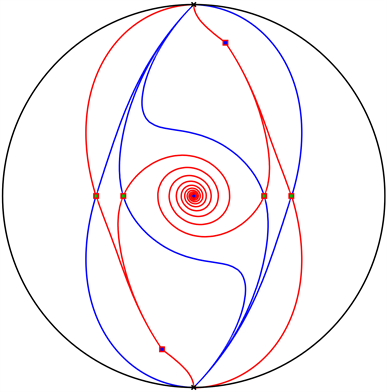
Figure 4. Global phase portraits of system (2) for $a=-1,b=0.2$

图4. 系统(2)在 $a=-1,b=0.2$ 时的全局相图

3. 结论

基于常微分方程的奇点理论和Poincaré紧致化，本文主要研究了一类在实际工程中具有广泛应用价值的五次非线性系统的全局动力学行为，该系统的动力学行为极其丰富，存在11个有限远平衡点，其中6个为不稳定的鞍点，3个为稳定的焦点，2个为稳定的结点；此外，该系统在Poincaré的 $U_1$ 盘上不存在无穷远平衡点，在 $U_2$ 盘上存在非初等奇点。我们注意到原系统在 $a\ge 0$ 时的动力学行为虽然得到了较多学者的关注，但几乎都是局部特性或是通过半分析的方法得到的近似解析的结果；当 $a<0$ 时的情形由于其异常复杂的动力学行为，鲜见有关学者进行研究，所以我们的结果可为人们进一步认识此类五次非线性系统的全局动力学行为提供借鉴。

基金项目

国家自然科学基金项目(No.11672259)和国家留学基金项目(No.201908320086)资助。