非线性色散方程的局部间断Petrov-Galerkin 方法

A Local Discontinuous Petrov-Galerkin Method for Nonlinear Dispersive Equations

摘要: 本文给出数值求解非线性色散偏微分方程K(n, n)的一种方法。空间离散基于局部间断Petrov-Galerkin方法，时间离散基于三阶TVD Runge-Kutta方法。通过数值模拟试验证明该方法达到了最优收敛阶，能够较好地模拟紧孤子传播和碰撞等复杂波的相互作用。

Abstract: In this paper, a numerical scheme is presented to solve the nonlinear dispersive K(n, n) equations. Spatial discretization is based on the local discontinuous Petrov-Galerkin method and temporal discretization is based on the third order accurate TVD Runge-Kutta scheme. Testing cases show that the present scheme achieves the optimal convergence order and complex wave interaction can be simulated well.

1. 引言

非线性色散方程K(m,n)

$u_t+{\left(u^m\right)}_x+{\left(u^n\right)}_{xxx}=0,m\ge 0,1<n\le 3$

此方程最早由Rosenau等 [1] 提出，对于给定的m和n，方程K(m, n)具有紧支集的孤立波解，即紧孤子。紧孤子结构与孤立子相似，其解有相似的运动状态。

紧孤子的常见数值模拟方法之一为谱方法 [2]，但是为了消除解在非光滑界面上产生的Gibbs振荡必须使用滤波器，这样就有可能错误地消除了某些高频物理振荡从而降低了解的精度。文 [3] [4] 使用了有限差分方法进行数值求解。Chertock [5] [6] 在Degond [7] 的基础上使用粒子方法来数值求解紧孤子方程的解，其优点是不必担心由于虚假的数值振荡造成其解改变轨迹并移动到错误的值域。Yan和Shu [8] [9] [10] 构造了局部间断Galerkin方法(Local Discontinuous Galerkin Method, LDG)并对非线性色散方程K(m, n)进行求解，给出了单元界面合适的数值流通量，构造了小扰动线性稳定格式，数值实验表明解中同时存在间断和高频振荡时，LDG方法更具优势。

基于间断Galerkin方法 [11] - [17]，广义差分法 [18] 和控制体积有限元方法 [19] [20]，Chen和Yu构造了控制体积间断有限元方法 [21] [22]，在此基础上Zhao和Yu [23] [24] 又给出了局部间断Petrov-Galerkin (Local Discontinuous Petrov Galerkin Method, LDPG)方法。LDPG方法在保持DG方法的优点基础上，具有天然的保持局部守恒性质，比DG方法更易构造和计算机实现。本文将使用LDPG方法对非线性色散方程K(n,n)进行数值求解，并给出算例加以验证该方法的可靠性。

2. 格式的构造

2.1. 空间离散

非线性色散方程

$\{\begin{array}{l}{u}_t+{\left(u^n\right)}_x+{\left(u^n\right)}_{xxx}=0,a\le x\le b,0<t\le T\\ u\left(x,0\right)=u_0\left(x\right)\end{array}$ (1)

通过引入辅助变量可将方程(1)改写成一阶方程组

$\{\begin{array}{l}{u}_t+{\left(v+p\right)}_x=0\\ p-q_x=0\\ q-v_x=0\\ v-u^n=0\end{array}a\le x\le b,0<t\le T$ (2)

首先对求解区域 $\left[a,b\right]$ 进行剖分， $a=x_{-1/2}<x_{1/2}<\cdots <x_{N-1/2}=b$, 其中 $x_{j-1/2}\left(0\le j\le N\right)$ 为求解区间的剖分节点，并定义控制单元 $I_j=\left(x_{j-1/2},x_{j+1/2}\right)$，且

$\begin{array}{l}{x}_j=\left(x_{j-1/2}+x_{j+1/2}\right)/2,\Delta x_j=x_{j+1/2}-x_{j-1/2},\\ f_{j-1/2}^{+}=\underset{x\to x_{j-1/2}^{+}}{\lim }f\left(x\right),f_{j-\text{1/2}}^{-}=\underset{x\to x_{j-1/2}^{-}}{\lim }f\left(x\right),h=\underset{0\le j\le N}{\max }\Delta x_j\end{array}$

选取控制单元

$I_j^1=\left(x_{j-1/2},x_{j-1/2}+\frac{1}{4}\Delta x\right),I_j^2=\left(x_{j-1/2}+\frac{1}{4}\Delta x,x_{j+1/2}-\frac{1}{4}\Delta x\right),I_j^3=\left(x_{j+1/2}-\frac{1}{4}\Delta x,x_{j+1/2}\right)$

$I_j$ 上的试探函数空间 $V_h$ 相应基函数为

${\phi }_j^{\left(0\right)}\left(\xi \right)=2\xi \left(\xi -\frac{1}{2}\right),{\phi }_j^{\left(1\right)}\left(\xi \right)=-4\left(\xi -\frac{1}{2}\right)\left(\xi +\frac{1}{2}\right),{\phi }_j^{\left(2\right)}\left(\xi \right)=2\xi \left(\xi +\frac{1}{2}\right)$

因此单元形状函数可以表示为 $u_h\left(x,t\right)={\displaystyle \underset{l=0}{\overset{2}{\sum }}{u}_j^l{\phi }_j^{\left(l\right)}\left(\xi \right)}$，其中 $\xi =\frac{x-x_j}{h}$。

对于LDPG而言，控制单元 $I_j^1,I_j^2,I_j^3$ 上检验函数是一个分段常数函数

${\psi }_j^l=\{\begin{array}{l}1,\forall x\in I_j^l\\ 0,\text{otherwise}\end{array},l=1,2,3$

将方程组(2)两边同时乘以检验函数 ${\psi }_j^l$，并在 $I_j^l$ 上积分， $l=1,2,3$，可以得到

${\displaystyle {\int }_{I_j^l}{u}_t{\psi }_j^l\text{d}x}+{\displaystyle {\int }_{I_j^l}{\left(v+p\right)}_x{\psi }_j^l\text{d}x}=0$ (3)

${\displaystyle {\int }_{I_j^l}p{\psi }_j^l\text{d}x}+{\displaystyle {\int }_{I_j^l}{q}_x{\psi }_j^l\text{d}x}=0$ (4)

${\displaystyle {\int }_{I_j^l}q{\psi }_j^l\text{d}x}+{\displaystyle {\int }_{I_j^l}{v}_x{\psi }_j^l\text{d}x}=0$ (5)

检验函数用相应基函数代替， $v,p,q,u$ 用 $v_h,p_h,q_h,u_h\in V_h$ 代替得到

${\displaystyle {\int }_{I_j^l}{\left(u_h\right)}_t\text{d}x}+{\displaystyle {\int }_{I_j^l}{\left(v_h+p_h\right)}_x\text{d}x}=0$ (6)

${\displaystyle {\int }_{I_j^l}{p}_h\text{d}x}+{\displaystyle {\int }_{I_j^l}{\left(q_h\right)}_x\text{d}x}=0$ (7)

${\displaystyle {\int }_{I_j^l}{p}_h\text{d}x}+{\displaystyle {\int }_{I_j^l}{\left(q_h\right)}_x\text{d}x}=0$ (8)

利用积分公式得

$\left(\begin{array}{c}\frac{\text{d}{u}_j^0}{\text{d}t}\\ \frac{\text{d}{u}_j^1}{\text{d}t}\\ \frac{\text{d}{u}_j^2}{\text{d}t}\end{array}\right)=A^{-1}\left(\begin{array}{c}-\left[{\left(v_h+p_h\right)}_{j-1/2+1/4\Delta x}-{\left({\tilde{v}}_h+{\hat{p}}_h\right)}_{j-1/2}\right]\\ -\left[{\left(v_h+p_h\right)}_{j+1/2-1/4\Delta x}-{\left(v_h+p_h\right)}_{j-1/2+1/4\Delta x}\right]\\ -\left[{\left({\tilde{v}}_h+{\hat{p}}_h\right)}_{j+1/2}-{\left(v_h+p_h\right)}_{j-1/2+1/4\Delta x}\right]\end{array}\right)$ (9)

$\left(\begin{array}{c}{p}_j^{\text{0}}\\ p_j^{\text{1}}\\ p_j^{\text{2}}\end{array}\right)=A^{-1}\left(\begin{array}{c}{\left(q_h\right)}_{j-1/2+1/4\Delta x}-{\left({\hat{q}}_h\right)}_{j-1/2}\\ {\left(q_h\right)}_{j+1/2-1/4\Delta x}-{\left(q_h\right)}_{j-1/2+1/4\Delta x}\\ {\left({\hat{q}}_h\right)}_{j+1/2}-{\left(q_h\right)}_{j+1/2-1/4\Delta x}\end{array}\right)$ (10)

$\left(\begin{array}{c}{q}_j^0\\ q_j^1\\ q_j^{\text{2}}\end{array}\right)=A^{-1}\left(\begin{array}{c}{\left(v_h\right)}_{j-1/2+1/4\Delta x}-{\left({\hat{v}}_h\right)}_{j-1/2}\\ {\left(v_h\right)}_{j+1/2-1/4\Delta x}-{\left(v_h\right)}_{j-1/2+1/4\Delta x}\\ {\left({\hat{v}}_h\right)}_{j+1/2}-{\left(v_h\right)}_{j+1/2-1/4\Delta x}\end{array}\right)$ (11)

其中

$A=\left(\begin{array}{ccc}\frac{1}{\text{6}}& \frac{\text{5}}{\text{48}}& \frac{-1}{\text{48}}\\ \frac{1}{\text{48}}& \frac{\text{11}}{\text{24}}& \frac{1}{\text{48}}\\ \frac{-1}{\text{48}}& \frac{\text{5}}{\text{48}}& -\frac{\text{1}}{\text{6}}\end{array}\right)$， $A^{-1}=\left(\begin{array}{ccc}\frac{19}{3}& \frac{-5}{3}& 1\\ \frac{-1}{3}& \frac{7}{3}& \frac{-1}{3}\\ 1& \frac{-5}{3}& \frac{19}{3}\end{array}\right)$

空间离散完毕，可得常微分方程组

$\{\begin{array}{l}\frac{\text{d}{u}_h}{\text{d}t}=A^{-1}G\left(v_h,p_h\right)\\ p_h=A^{-1}G\left(q_h\right)\\ q_h=A^{-1}G(\; v\; h\; )\end{array}$

上式中 $\hat{p},\hat{q},\hat{v}$ 为数值流通量，在这里使用“交替型数值流通量” [10]。对于K(m, n)方程，若n为奇数，数值流通量做如下选取

${\hat{p}}_h=p_h^{+},{\hat{q}}_h=q_h^{+},{\hat{v}}_h=v_h^{-}$

若n为偶数，数值流通量做如下选取

$\begin{array}{l}{\hat{p}}_h=p_h^{+},{\hat{v}}_h=v_h^{\text{+}}\\ {\hat{q}}_h=\{\begin{array}{l}{q}_h^{+},\text{if}{\left(u_h^{+}\right)}^{n-1}+{\left(u_h^{-}\right)}^{n-1}\ge 0\\ q_h^{-},\text{otherwise}\end{array}\end{array}$

流通量 ${\tilde{v}}_h$ 为局部Lax-Friedrichs数值流通量

$\hat{f}\left(u^{-},u^{+}\right)=\frac{1}{2}\left[f\left(u^{-}\right)+f\left(u^{+}\right)-\alpha \left(u^{+}-u^{-}\right)\right]$

其中

$\alpha =\underset{u\in \Omega }{\max }\left|f^{\prime }\left(u\right)\right|,\Omega =\left[\min \left(u^{-},u^{+}\right),\max \left(u^{-},u^{+}\right)\right]$

2.2. 时间离散

经过空间离散后的常微分方程组，利用三阶TVD Runge-Kutta方法来求解。令

$\frac{\text{d}{U}_h}{\text{d}t}=L_h\left(U_h,t\right)$

其中

$L_h\left(U_h,t\right)=A^{-1}G\left(V_h,P_h\right)$

则有

$\{\begin{array}{l}{u}^{\left(1\right)}=u^n+\Delta tL\left(u^n,t_n\right)\\ u^{\left(2\right)}=\frac{3}{4}{u}^n+\frac{1}{4}\left(u^{\left(1\right)}+\Delta tL\left(u^{\left(1\right)},t_n+\Delta t\right)\right)\\ u^{n+1}=\frac{1}{3}+\frac{2}{3}\left(u^{\left(2\right)}+\Delta tL\left(u^{\left(2\right)},t_n+\Delta t\right)\right)\end{array}$

3. 算例

3.1. 算例1线性色散方程(表1)

$u_t+u_{xxx}=0,\text{0}\le x\le 2\pi ,0<t\le T$ (12)

$u\left(x,0\right)=\sin \left(x\right),0\le x\le 2\pi$ (13)

边界条件

$u\left(0,t\right)=\sin \left(t\right),u\left(2\pi ,t\right)=\sin \left(2\pi +t\right)$

表1. 例1分别使用 $P^1,P^2$ 元在t = 1时的精度及误差

Table1. $L_1,L_2$ and $L_{\infty }$ errors at time=1 with $P^1$ and $P^2$ for case 1

$\begin{array}{llllllll}\hfill & grid\hfill & L_1\hfill & order\hfill & L_2\hfill & order\hfill & L_{\infty }\hfill & order\hfill \\ P^1\hfill & 20\hfill & 2.6509\times {10}^{-2}\hfill & \hfill & 1.1732\times {10}^{-2}\hfill & \hfill & 6.5971\times {10}^{-3}\hfill & \hfill \\ \hfill & 40\hfill & 6.6391\times {10}^{-3}\hfill & 1.9975\hfill & 2.9480\times {10}^{-3}\hfill & 1.9926\hfill & 1.6030\times {10}^{-3}\hfill & 2.0405\hfill \\ \hfill & 80\hfill & 1.6569\times {10}^{-3}\hfill & 2.2024\hfill & 7.3735\times {10}^{-4}\hfill & 1.9993\hfill & 3.8496\times {10}^{-4}\hfill & 2.0580\hfill \\ \hfill & 160\hfill & 4.1352\times {10}^{-4}\hfill & 2.0025\hfill & 1.8429\times {10}^{-4}\hfill & 2.0003\hfill & 9.7907\times {10}^{-5}\hfill & 1.9752\hfill \\ P^2\hfill & 10\hfill & 4.2531\times {10}^{-3}\hfill & \hfill & 3.3619\times {10}^{-3}\hfill & \hfill & 1.2432\times {10}^{-3}\hfill & \hfill \\ \hfill & 20\hfill & 5.0078\times {10}^{-4}\hfill & 3.0862\hfill & 4.0071\times {10}^{-4}\hfill & 3.0686\hfill & 1.4864\times {10}^{-4}\hfill & 3.0641\hfill \\ \hfill & 40\hfill & 6.1521\times {10}^{-5}\hfill & 3.0250\hfill & 4.9254\times {10}^{-5}\hfill & 3.0242\hfill & 1.8913\times {10}^{-5}\hfill & 2.9743\hfill \\ \hfill & 80\hfill & 7.6752\times {10}^{-6}\hfill & 3.0028\hfill & 6.1174\times {10}^{-6}\hfill & 3.0093\hfill & 2.4109\times {10}^{-6}\hfill & 2.9717\hfill \end{array}$

3.2. 算例2 非线性色散方程K(3, 3)

$u_t+{\left(u^3\right)}_x+{\left(u^3\right)}_{xxx}=0$ (14)

初始条件

$u_0=\{\begin{array}{l}2\cos \left(\frac{x}{5}\right)x\in \left[-2.5\pi ,2.5\pi \right]\\ 0\text{else where}\end{array}$ (15)

模拟结果如下图1，我们选取200个单元格以及 $P^{\text{2}}$ 元LDPG与LDG方法进行比较。

从图像可以看出，随着时间推移，一列紧孤子从初始波形分裂出来向右移动，在初始波形的左侧出现了高频震荡，这说明使用局部间断Petrov-Galerkin方法可以同时捕捉到尖锐的界面和高频振荡，这在伪谱方法中是无法实现的，证实了LDPG的稳定性和精度。

使用初始条件

$u_0=\{\begin{array}{l}\sqrt{\frac{3}{2}}\cos \left(\frac{x}{6}\right)x\in \left[-\text{3}\pi ,\text{3}\pi \right]\\ 0\text{else where}\end{array}$ (16)

Figure 1. The K(3, 3) equation (14). Compactons splitting from the initial data (15) at selected time

图1. K(3, 3)方程(14)使用初值(15)在不同时刻的解

也观察到类似的振荡情况，如图2：

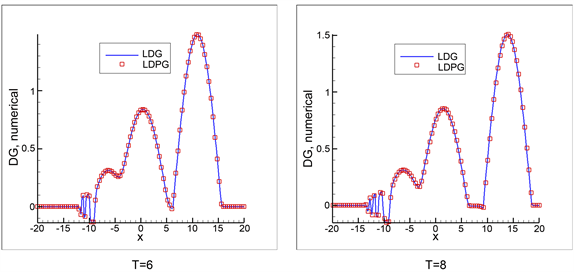
Figure 2. The K(3, 3) equation (14). Compactons splitting from the initial data (16) at selected time

图2. K(3, 3)方程(14)使用初值(16)在不同时刻的解

3.3. 算例3非线性色散方程K(2, 2)

$u_t+{\left(u^{\text{2}}\right)}_x+{\left(u^{\text{2}}\right)}_{xxx}=0$ (17)

初始条件

$u_0=\{\begin{array}{l}\frac{\text{4}}{\text{3}}{\cos }^{\text{2}}\left(\frac{x}{\text{8}}\right)x\in \left[-4\pi ,4\pi \right]\\ 0\text{else where}\end{array}$ (18)

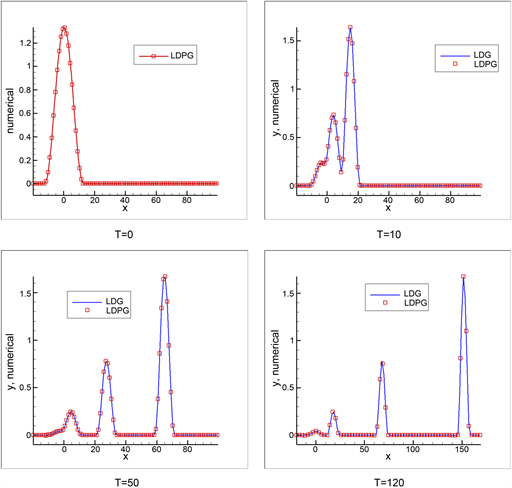
Figure 3. The K(3, 3) equation (14). Compactons splitting from the initial data (15) at selected time

图3. K(3, 3)方程(14)使用初值(15)在不同时刻的解

如图3我们依旧选取200个单元格以及 $P^{\text{2}}$ 元来模拟不同时刻紧孤子碰撞情况，并与LDG方法模拟情况作对比。

4. 结论

本文利用局部间断Petrov-Galerkin方法对非线性色散方程K(n, n)进行了数值求解，分别模拟了n为奇数和偶数两种紧孤子运动状态。根据n的奇偶性选取适当的数值流通量以得到更稳定的数值格式。数值实验证明，该方法的数值结果可以精准的描述紧孤子演化过程，对于求解更复杂的高阶方程具有较好参考意义。

基金项目

内蒙古大学科研发展基金(21100-5187133)；内蒙古自治区人才开发基金项目(12000-1300020240)。