CAARC模型间距对缝隙流流场特性的影响

The Effect of CAARC Model Spacing on the Characteristics of Slit Flow

摘要: 为了研究建筑物间距对流场特性的影响，本次试验采用两个缩尺比同为1:100的CAARC模型，通过改变两个CAARC模型的间距比，运用三维脉动风速仪测得了风速时程，进而得到了不同间距比和高度比下并列CAARC模型周围流场的湍流积分尺度和湍流强度。并对各个测点处的湍流强度和湍流积分尺度进行了分析。结果表明：测点4处的积分尺度随模型距比增大而减小，湍流强度随模型间距比增大而增大；测点1、测点2、测点3的积分尺度随模型间距比增大而增大，湍流度随模型间距比增大而减小。

Abstract: In order to study the influence of building spacing on the flow field characteristics, two CARRC mod-els with the same scale ratio of 1:100 were adopted in this experiment. By changing the spacing ra-tio of the two CARRC models, the wind speed time history can be obtained by utilizing the three-dimensional pulsating anemometer. Then, the turbulence integral scale and turbulence in-tensity of the flow field around the parallel CARRC model can be presented under different spacing ratio and height ratio. The turbulence intensity and turbulence integral scale at each measuring point were analyzed. Based on the experimental data, the following conclusion can be drawn: with the increase of model spacing ratio, the turbulence integral scale at measuring point 4 decreased and the turbulence intensity increased. Conversely, the turbulence integral scales at measuring point 1, measuring point 2 and measuring point 3 increased with the increase of model spacing ra-tio, and the turbulence intensity decreased with the increase of model spacing ratio.In order to study the influence of building spacing on the flow field characteristics, two CAARC mod-els with the same scale ratio of 1:100 were adopted in this experiment. By changing the spacing ra-tio of the two CAARC models, the wind speed time history can be obtained by utilizing the three-dimensional pulsating anemometer. Then, the turbulence integral scale and turbulence in-tensity of the flow field around the parallel CAARC model can be presented under different spacing ratio and height ratio. The turbulence intensity and turbulence integral scale at each measuring point were analyzed. Based on the experimental data, the following conclusion can be drawn: with the increase of model spacing ratio, the turbulence integral scale at measuring point 4 decreased and the turbulence intensity increased. Conversely, the turbulence integral scales at measuring point 1, measuring point 2 and measuring point 3 increased with the increase of model spacing ra-tio, and the turbulence intensity decreased with the increase of model spacing ratio.

1. 引言

并列双柱在实际工程中应用较多，比如并列的烟囱和高层建筑。由于两栋相邻建筑之间存在流场干扰，因此相对于单栋建筑的绕流流场，其流场特性会复杂许多。而流场特性的不同对于建筑物的表面风压和风振响应有着重要影响，因此研究双柱绕流对实际工程应用有重大意义。鉴于此，国内外众多学者对此进行了相关研究，其研究方法主要通过风洞试验和数值模拟展开。

陈素琴等 [1] 通过数值模拟的方法，研究了并列双方柱间距比不同时流场的变化情况，结果表明并列双方柱在间距比小于临界间距比时两柱之间的缝隙流会出现双稳态偏流现象，并且当发生偏流时偏流边的柱体相比于非偏流边的柱体具有更大的升力和阻力。盛奇伟 [2]、饶勇等 [3] 和马金英 [4] 也通过数值模拟方法发现了双稳态偏流现象的存在。吴倩云等 [5] 通过风洞试验方法分析了并列双柱间距比对风压系数和升阻力系数的影响，结果表明当间距比1.2 ≤ L/D ≤ 2.5时，其对并列方柱的平均风压系数的影响明显；当L/D ≥ 2.5时，其对平均风压系数、平均阻力系数和脉动升力系数的影响均不明显。韩宁等 [6] 通过风洞试验研究了间距比对两并列高层建筑局部风压干扰特性的影响，结果表明随着间距比的增大，平均风压系数和脉动风压系数的干扰因子的最大值在狭缝面和外侧面均呈现出减小的趋势，在迎风侧和背风侧呈现出增大的趋势。Karthik等 [7] 等通过数值模拟的方法研究了间距比对并列双柱横风下风振的影响，结果表明，与较小的间距比相比，间距比(L/D = 4.5)的柱体产生的响应最小。Yen等 [8] 通过改变双方柱的间距比，对双方柱后的尾流结构进行了划分。王小华等 [9] 通过大涡模拟的方法发现在边界条件完全对称的情况下，对称点的压应力频谱并不相同。魏英杰等 [10] 通过大涡模拟的方法发现在对称边界条件下，双方柱绕流运动参量的时域过程虽然是不对称的，但频域过程却是对称的。赵小军等 [11] 通过大涡模拟方法，研究了方柱绕流的速度场和涡量场。谢壮宁等 [12] 通过风洞试验方法，比较了三并列方柱与双并列方柱在不同间距比下的干扰效应，结果表明并列三方柱间的干扰响应明显高于双方柱并列。

前人的研究多为并列双柱间距比对流场形态、双柱风压系数与升阻力系数以及对风振响应的影响，很少研究间距比对两柱之间缝隙流脉动风参数的影响。因此，本文通过风洞试验，对并列双柱缝隙流的脉动风参数进行了研究，得到了不同高度比下脉动风参数随间距比变化的规律。

2. 试验概况

2.1. 风场模拟

试验在西南交通大学XNJD-3大气边界层风洞中完成，该风洞建成于2008年，是一座回流式低速风洞，其各项技术指标均达到世界先进水平，也是目前世界上最大的边界层风洞。风洞试验段长36米，宽22.5米，高4.5米，风速范围从1.0 m/s至16.5 m/s连续可调。采用尖劈、挡板与粗糙元技术模拟地表风场，利用三维脉动风速仪测量风速时程，风速仪采样频率为1024 Hz，采样时长为120 s。根据《建筑工程风洞试验方法标准》(JGJ/T338-2014) [13]，B类风场平均风速剖面指数α取0.15，对应来流的风速剖面和湍流度剖面的模拟结果如图1。由图1可知，在试验高度范围内除在局部试验值偏离标准值外，总体上与标准值相吻合，可视为满足规范要求。其中U为Z高度处的平均风速，U_2H/3为参考高度处的平均风速，参考高度为2H/3，H为模型高度。

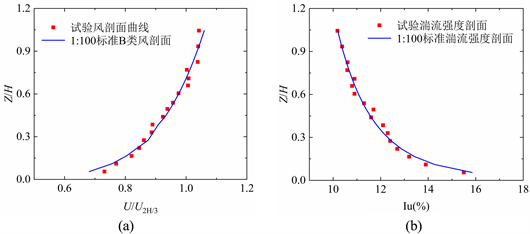
Figure 1. Average wind speed profile and turbulence intensity profile. (a) Average wind speed profile; (b) Turbulence intensity profile

图1. 平均风速剖面与湍流度剖面。(a) 平均风速剖面；(b) 湍流度剖面

2.2. 模型设计与工况布置

本次试验采用两个CAARC标准模型，制作材料为普通木材，通过在内部设置加劲肋以保证其刚度，试验模型几何缩尺比为1:100，模型尺寸为45.72 cm (D) × 30.48 cm (B) × 182.88 cm (H)。图2为试验模型。本次试验均在0˚风向角下进行，并且两个模型均选择长边为迎风面，采用五个不同的模型间距，分别为0.3 m、0.5 m、0.8 m、1.0 m和1.2 m，则每个间距对应的间距比L/D为0.66、1.09、1.75、2.19和2.62。本次试验共布置了六个测点，其测点布置如图3所示。其中0号测点为来流方向未受到模型干扰的位置，测点1、测点2、测点3、测点4和测点5的两两间距均为B/2，B为模型宽度，测点4为模型间距的正中心位置，测点3为模型间距前缘的中点，测点5为模型间距后缘的中点。分别测得了每个测点在各个间距下4个不同高度处的风速时程，高度h分别为1/4H、1/2H、2/3H和H。

Figure 2. Wind tunnel test model

图2. 风洞试验模型

Figure 3. Layout of measuring points

图3. 测点布置图

3. 试验参数定义

3.1. 湍流积分尺度

湍流涡旋在大气边界层中可以被视为频率为n的周期脉动，与波相似，定义涡旋的波长λ = U/n，其中U为平均风速，那么涡旋大小的尺度就是波长。脉动风中湍流涡旋平均尺寸的量度是湍流积分尺度，对应于与纵向、横向和垂直方向脉动速度分量u、v和w有关的三个方向，一共有9个湍流积分尺度，例如 $L_u^x$ 、 $L_u^y$ 和 $L_u^z$ 分别量度与纵向脉动速度有关的涡旋在纵向、横向和垂直方向的平均尺寸。在数学上可以定义 $L_u^x$ 为

$L_u^x=\frac{1}{{\sigma }_u^2}{\displaystyle {\int }_0^{\infty }{R}_{12}\left(x\right)dx}$ (1)

式中： $R_{12}\left(x\right)$ 为两个不同空间位置上纵向脉动速度 $u_1=u\left(x_1,y_1,z_1,t\right)$ 和 $u_2=u\left(x_1+x,y_1,z_1,t\right)$ 的互协方差函数，t为时间； ${\sigma }_u^2$ 为脉动速度u的方差； $R_{12}\left(0\right)={\sigma }_u^2$。同样的定义也适用于其它方向的湍流积分尺度。

湍流积分尺度是关于湍流空间相关性的参数，最好的方法是通过对空间多点进行同步测量，然后利用湍流积分尺度的定义计算，然而这种方法通常难以实现。因此在实际计算中，我们通常采用Taylor假设将多点测量转换为单点测量，将空间不同点的互相关函数转换成单点测量的自相关函数。Taylor假设的定义如下：

如果湍流涡旋以平均风速U迁移，则脉动速度 $u\left(x_1,t+\tau \right)$ 可以定义为 $u\left(x_1-x,\tau \right)$， $x=Ut$，这就是Taylor假设。根据Taylor假设，式(1)可改写为

$L_u^x=\frac{U}{{\sigma }_u^2}{\displaystyle {\int }_0^{\infty }{R}_u\left(\tau \right)\text{d}\tau }$ (2)

式中： $R_u\left(\tau \right)$ 为脉动风速 $u\left(x_1,t+\tau \right)$ 的自相关函数， $R_u\left(0\right)={\sigma }_u^2$。同理可求 $L_v^x$ 和 $L_w^x$。Flay等 [14] 认为式(2)的积分上限取到自相关系数降到0.05的点最佳。并且庞加斌等 [15] 通过风洞试验证明了Taylor假设在大气边界层中是合理的，采用自相关函数直接积分的方法计算湍流积分尺度渐变可靠。因此本文也采用基于Taylor假设的自相关函数算法计算湍流积分尺度。

3.2. 湍流强度

湍流强度反映了脉动风的强度，湍流强度可以分别在3个正交方向上定义，但是一般认为顺风向湍流强度在大气边界层中比其他两个分量大。因此本文主要考虑顺风向湍流强度，风速仪记录的统计表明，脉动风速均方根与平均风速成比例，因此，定义顺风向湍流强度为

$I_u=\frac{{\sigma }_u}{U}$ (3)

4. 实验结果与讨论

为了方便比较模型影响范围内的脉动风参数和未受模型影响的脉动风参数(测点0处的脉动风参数)的差异，在这里给出不同间距对于脉动风参数的干扰因子IF，定义如下：

$IF=\frac{受模型影响的脉动风参数}{未受模型影响的脉动风参数}$

干扰因子IF大于1表示模型的存在导致脉动风参数在增大，干扰因子IF小于1表示模型的存在导致脉动风参数在减小。

4.1. 各测点积分尺度变化

4.1.1. 沿顺风向积分尺度的变化

由于模型的存在，沿顺风向的湍流积分尺度会发生改变。图4给出了在高度比h/H = 0.5时不同测点位置处的湍流积分尺度干扰因子IF。图4表明，当高度比h/H = 0.5时在各个模型间距比下积分尺度均沿顺风向呈现出先增大后减小的趋势，并且均在测点4处取得最大值，在其他高度比时也有相似的规律。

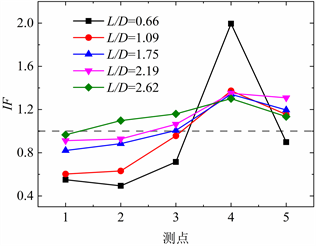
Figure 4. The integral scale of each point along the downwind direction

图4. 沿顺风向各点积分尺度

4.1.2. 间距对各个测点积分尺度的影响

图5给出了各个测点在4个高度比下积分尺度干扰因子IF随模型间距比的变化情况。测点1、测点2和测点3处的IF在各个高度比下均随模型间距比增大而增大；在0.66 ≤ L/D ≤ 1.75范围内变化较为明显，而在1.75 ≤ L/D ≤ 2.62范围内变化较为平缓；在高度比h/H=1时，IF最大，在高度比h/H = 0.5时，IF最小；且IF逐渐从小于1增大到略微大于1。测点4处的IF在各个高度比下均随模型间距比增大而减小；在0.66 ≤ L/D ≤ 1.75范围内变化较为明显，而在1.75 ≤ L/D ≤ 2.62范围内变化较为平缓；且IF在各个高度比下均大于1。当h/H = 0.25时，测点5处的IF随模型间距比增大而增大，且在0.66 ≤ L/D ≤ 1.09范围内变化明显，在1.09 ≤ L/D ≤ 2.62范围内变化较为平缓；当h/H > 0.25时，IF随模型间距比的增大呈现出先增大后减小的趋势。

(a) (b) (c) (d) (e)

Figure 5. Downwind integral scale of each measuring point. (a) Measuring point 1; (b) Measuring point 2; (c) Measuring point 3; (d) Measuring point 4; (e) Measuring point 5

图5. 各测点顺风向积分尺度。(a) 测点1；(b) 测点2；(c) 测点3；(d) 测点4；(e) 测点5

4.2. 各测点湍流度变化

4.2.1 . 沿顺风向湍流强度的变化

由于建筑物的干扰，沿顺风向的湍流强度会发生改变。图6给出了在高度比h/H = 0.5时各个模型间距比对各个测点湍流强度干扰因子IF的影响。图6表明，当高度比h/H = 0.5时在各个模型间距比下积分尺度均沿顺风向呈现出先减小后增大的趋势，并且在均在测点4处取得最小值，其他高度比情况下结果与此类似。

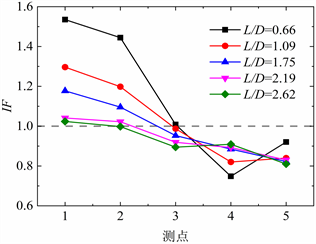
Figure 6. Turbulence intensity at each point along the downwind direction

图6. 沿顺风向各点湍流度

4.2.2 . 间距对各个测点湍流强度的影响

图7给出了各个测点在4个高度比下湍流强度干扰因子IF随模型间距比的变化情况。测点1和测点2处的IF在各个高度比下均随模型间距比增大而减小，且在0.66 ≤ L/D ≤ 1.09范围内变化较为明显，而在1.09 ≤ L/D ≤ 2.62范围内变化较为平缓；IF从大于1逐渐减小到略小于1；在高度比h/H = 0.5时，

(a) (b) (c) (d) (e)

Figure 7. Downwind turbulence intensity of each measuring point. (a) Measuring point 1; (b) Measuring point 2; (c) Measuring point 3; (d) Measuring point 4; (e) Measuring point 5

图7. 各测点顺风向湍流强度。(a) 测点1；(b) 测点2；(c) 测点3；(d) 测点4；(e) 测点5

IF最大，在高度比h/H = 1时，IF最小。测点3和测点5处的IF在各个高度比下均随模型间距比增大而减小，且在0.66 ≤ L/D ≤ 1.09范围内变化较为明显，而在1.09 ≤ L/D ≤ 2.62范围内变化较为平缓；测点3在各个高度比下IF均从略大于1减小到小于1，测点5在除高度比h/H = 1时IF均小于1。当h/H ≤ 0.67时，测点4处的IF随模型间距比增大而增大，IF均小于1，且在0.66 ≤ L/D ≤ 1.09范围内变化明显；当h/H = 1时，测点4处的IF随模型间距比增大呈现出先增大后减小的趋势，且IF均略大于1。

5. 结论

本文通过风洞试验的方法，对5种不同间距比的并列双柱进行了试验，通过对各个测点在不同工况下的湍流积分尺度与湍流强度的对比，可得出如下结论：

1) 测点1、测点2和测点3在各个高度比下的积分尺度均随模型间距比增大而增大，测点4处积分尺度随模型间距比增大而减小；当L/D ≤ 1.75时，各个测点积分尺度受模型间距比影响较大。

2) 测点1、测点2、测点3和测点5在各个高度比下的湍流强度均随模型间距比增大而减小；当h/H ≤ 0.67时，测点4处积分尺度随模型间距比增大而增大。当L/D ≤ 1.09时，各个测点湍流强度受模型间距比影响较大。

3) 从测点1到测点5，湍流积分尺度先增大后减小，且测点4处湍流积分尺度最大；湍流强度先减小后增大，且测点4处湍流强度最小。

上述研究结果为进一步研究发生钝体绕流时钝体周围的流场特性提供了一定的参考作用。

参考文献