基于晶格动力学的硅单晶热学性质研究(IV)——数值计算与低温负热膨胀机制研究

Study on Thermal Properties of Silicon Single Crystal Based on Lattice Dynamics (IV)—Numerical Calculation and Study on Mechanics of Negative Thermal Expansion at Low Temperature

摘要: 本文先求解硅单晶的晶格动力学矩阵的本征值问题，得到和谐近似下的晶格振动频率和位移，然后在此基础上运用基于晶格动力学及量子力学推导得到的热膨胀系数公式进行数值计算。数值计算结果表明，硅单晶的热膨胀系数主要由两个部分构成，一部分与近邻原子间中心势能有关，提供正热膨胀系数的贡献；另一部分与近邻原子间的非中心势能有关，产生负热膨胀系数的贡献。当从温度0 K开始增加时，负热膨胀系数的增加快于正热膨胀系数的增加，因此总的热膨胀系数为负，并随温度增加负热膨胀性质更为显著；当温度超过80 K继续增加时，正热膨胀系数的增加快于负热膨胀的增加，此时虽然整体还呈现负热膨胀，但负热膨胀性质开始减弱；到约120 K温度时负热膨胀现象消失。本文还通过Rignanese等人计算得到的不同晶格常数下的线性力常数数据，发现硅单晶的三体势的三阶力常数为正，从而找到了支持我们早先提出的低温下硅单晶的负热膨胀的物理机制的直接证据。

Abstract: The lattice vibration frequency and displacement under harmonic approximation are obtained by solving the eigenvalue problem of lattice dynamics matrix of silicon single crystal, then the thermal expansion coefficients are calculated with the aid of the formula derived based on lattice dynamics and quantum mechanics. The numerical results show that the thermal expansion coefficient of silicon single crystal is mainly composed of two parts, one is positive, which is related to the central potential between the nearest atoms, and the other is negative, which is related to the non-central potential energy between the nearest atoms. When increasing temperature from 0K, the negative part increases faster than the positive part, so the total thermal expansion coefficient is negative and more significant with the increase of temperature; when temperature is exceeding80K, the positive part begins to increase faster than the negative part, so the negative thermal expansion property begins to weaken. At about 120 K, the negative thermal expansion disappears. With the aid of the linear force constants with different lattice constants calculated by Rignanese et al, it is found that the third order force constant of the three-body potential in silicon single crystal is positive. Thus, the direct evidence is found to support the physical mechanism of negative thermal expansion of silicon single crystal at low temperature suggested by us before.

1. 引言

运用晶格动力学和量子力学的微扰论，我们在先前已经得到了硅单晶的晶格常数热膨胀公式 [1]

$\Delta a=\frac{4}{3\left(8\mu +\alpha \right)}\left[\langle U\left(AO,{\alpha }^{\prime },{\beta }^{\prime }\right)\rangle +3\langle U_3\left(AB,{\nu }^{\prime },{\lambda }^{\prime }\right)\rangle \right]$ (1)

其中，

$\langle U\left(AO,{\alpha }^{\prime },{\beta }^{\prime }\right)\rangle =-\frac{1}{2}\left({\alpha }^{\prime }-{\beta }^{\prime }\right)\langle x_{OA}^2+y_{OA}^2+z_{OA}^2\rangle -\frac{1}{2}{\beta }^{\prime }\langle {\left(x_{AO}+y_{AO}+z_{AO}\right)}^2\rangle$ (2)

$\langle U_3\left(AB,{\lambda }^{\prime },{\nu }^{\prime }\right)\rangle =-\frac{1}{2}\langle {\lambda }^{\prime }{x}_{AB}^2+{\nu }^{\prime }{\left(y_{AB}+z_{AB}\right)}^2\rangle$ (3)

我们还得到了硅单晶的晶格常数热膨胀系数公式

$\gamma =\frac{4\hslash }{3Nm\left(8\mu +\alpha \right)a}\underset{kj}{{\displaystyle \sum }}\frac{{\rho }_{kj}}{{\omega }_{kj}}\frac{\partial {\bar{n}}_{kj}}{\partial T}$ (4)

其中， ${\bar{n}}_{kj}$ 为平均声子数， ${\rho }_{kj}$ 由下式计算

$\begin{array}{c}{\rho }_{kj}=-\frac{1}{2}\left({\alpha }^{\prime }-{\beta }^{\prime }\right)\underset{\sigma }{{\displaystyle \sum }}{\left|e_{\sigma }\left(O|kj\right)-e_{\sigma }\left(A|kj\right)\right|}^2-\frac{1}{2}{\beta }^{\prime }\langle {\left|\underset{\sigma }{{\displaystyle \sum }}{e}_{\sigma }\left(O|kj\right)-e_{\sigma }\left(A|kj\right)\right|}^2\rangle \\ -6\underset{kj}{{\displaystyle \sum }}\left\{{\lambda }^{\prime }{\left|e_x\left(A|kj\right)\right|}^2+{\nu }^{\prime }{\left|e_y\left(A|kj\right)+e_z\left(A|kj\right)\right|}^2\right\}{\sin }^2\frac{\left(k_y+k_z\right)a}{4}\end{array}$ (5)

根据Rignanese等人 [2] 通过第一性原理，计算得到的晶格常数a为10.18b和10.26b时的近邻原子间和次近邻原子间的力常数，我们求得这些力常数对晶格常数的导数即三阶力常数为 ${\alpha }^{\prime }=0.0200\text{h}/{\text{b}}^{\text{3}}$ 、 ${\beta }^{\prime }=0.02638\text{h}/{\text{b}}^{\text{3}}$ 、 ${\lambda }^{\prime }=-0.00062\text{h}/{\text{b}}^{\text{3}}$ 、 ${\nu }^{\prime }=0.00125\text{h}/{\text{b}}^{\text{3}}$ 。此处，h代表能量单位hartree， $1\text{hartree}=4.360\times {10}^{-18}\text{J}$ ，b代表长度单位bohr， $1\text{bohr}=0.5292\times {10}^{-10}\text{m}$ 。在求动力学矩阵时使用晶格常数a为10.18b时的线性力常数 $\alpha =-0.03385\text{h}/{\text{b}}^{\text{2}}$ 、 $\beta =-0.02348\text{h}/{\text{b}}^{\text{2}}$ 、 $\lambda =0.00433\text{h}/{\text{b}}^{\text{2}}$ 、 $\nu =-0.00178\text{h}/{\text{b}}^{\text{2}}$ 、 $\delta =0.00111\text{h}/{\text{b}}^{\text{2}}$ 和 $\mu =-0.00182\text{h}/{\text{b}}^{\text{2}}$ ，然后求解晶格动力学矩阵的本征值问题，即可得到 ${\omega }_{kj}$ 和原子A和O振动的单位极化矢量 $e\left(O|kj\right)$ 和 $e\left(A|kj\right)$ ，再将这些数据连同三阶力常数一起代入以上公式，即可方便地求得硅单晶地热膨胀系数。

由(1)式可知，硅单晶的晶格常数的热膨胀来自两部分的非线性相互作用的贡献，其中 $\langle U\left(AO,{\alpha }^{\prime },{\beta }^{\prime }\right)\rangle$ 对应于最近邻原子间非线性相互作用， $\langle U_3\left(AB,{\lambda }^{\prime },{\nu }^{\prime }\right)\rangle$ 对应于次近邻原子间非线性相互作用。由(2)式和(3)式可知，由于非线性力常数 ${\lambda }^{\prime }$ 和 ${\nu }^{\prime }$ 远小于 ${\alpha }^{\prime }$ 和 ${\beta }^{\prime }$ ，因此硅单晶的晶格常数的热膨胀主要来自于最近邻原子间的非线性相互作用，即可以忽略次近邻原子间非线性相互作用对晶格常数热膨胀的贡献。由(2)式知，最近邻原子间的非线性相互作用所产生的晶格常数热膨胀，可分为以下两个部分单独计算，即最近邻原子间非中心的和中心的非线性相互作用所产生的晶格常数热膨胀。通过以上公式，我们还可以单独计算和分析某个或某些三阶力常数对热膨胀系数的贡献，这对研究硅单晶的热膨胀性质，尤其对研究其低温负热膨胀性质物理机制，是非常有利的，这也是本理论方法相比于分子动力学(MD) [3] 和准谐近似(QHA) [4] 的显著优点。

根据文献 [5] 提供的公式，计算晶格动力学矩阵，求解晶格动力学矩阵的本征值问题，即可得到声子频谱及单位极化矢量，这些数据将会被应用到热膨胀计算。图1中展示了 $k_z=0$ 、 $k_x=k_y=k$ 时, 声子频率与 的色散关系。由图可知，在硅单晶体中，晶格振动由三个波矢为零时频率为零的声学支(对应于色散曲线1、2、3)和波矢为零时频率不为零的光学支(对应于色散曲线4、5、6)构成，与其它文献的结论一致。

2. 热膨胀系数计算

运用公式(4)和(5)，在温度从0 K到1200 K，计算了从晶格常数热膨胀及热膨胀系数随温度的变化关系，其结果如图2所示。为了验证计算结果的准确性，图中还展示了Ibach等人 [6] 的有关硅单晶体热膨胀系数随温度变化关系的实验测量结果。由图可知，我们的计算结果与Ibach等人的实验结果能很好地吻合，并且大约在0 K到120 K的低温段，再现了硅单晶体的负热膨胀这种奇异的热学性质，说明了我们提出的计算硅单晶体热膨胀性质计算的微扰论方法及结果是正确的。为了能在本文中对硅晶体在低温下的负热膨胀性质的物理机制进行深入探讨，在图2中还给出了最近邻原子间中心势、非中心势和次近邻原子间作用对热膨胀系数的贡献，它们三者之和即为硅单晶的热膨胀系数的计算总结果。

由于 ${\lambda }^{\prime }$ 和 ${\nu }^{\prime }$ 的绝对值远小于 ${\alpha }^{\prime }$ 和 ${\beta }^{\prime }$ 的绝对值，由(5)式可以推断，次近邻原子间相互作用引起的热膨胀可以忽略，图2所示。热膨胀主要由两个部分构成，一部分与(5)式中的第一项对应，由于 ${\alpha }^{\prime }-{\beta }^{\prime }$ 为正，因此非中心势能产生负热膨胀贡献。另一部分与(5)式中的第二项对应，由于 ${\beta }^{\prime }$ 为负值，因此中心势能产生正热膨胀贡献，如图2所示。在零温度下，由于 $\partial {\bar{n}}_j\left(k\right)/\partial T=0$ ，中心势能、非中心势能对热膨胀贡献均为0；温度从0 K上升，中心势能产生的热膨胀系数随温度的上升而增加，非中心势能产生的热膨胀系数随温度的上升而降低，由于后者降低的速度大于前者上升的速度，因此总体呈现负热膨胀系数，并随温度增加，总热膨胀系数负得越多；当温度到达80 K后进一步升高，中心势能产生的热膨胀系数增加加快，非中心势能产生的热膨胀系数降低趋缓，总体上硅单晶的负热膨胀效应减弱，并随温度进一步升高至约120 K时，总热膨胀系数开始变正；在温度达到400 K后，非中心势能产生的热膨胀系数随温度的升高而几乎不再增长，而中心势能产生的正热膨胀系数在增加，总体为正热膨胀系数随温度升高而增加；当温度达到800 K后，在高温近似下， $\partial {\bar{n}}_j\left(k\right)/\partial T=k_B/\hslash {\omega }_{kj}$ ，与温度无关，因此非中心势能和中心势能所产生负和正热膨胀系数也趋于恒定，总体为正的热膨胀系数几乎不再随温度增加而增加。

Figure 1. Phonon frequency vs. ka/2

图1. 声子频率与ka/2之间的关系

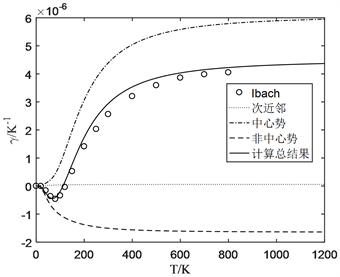
Figure 2. Thermal expansion coefficient of silicon single crystal vs. temperature

图2. 硅单晶热膨胀系数与温度之间关系

3. 低温下硅单晶体负热膨胀系数机制分析

为了进一步探讨硅单晶体的低温负热膨胀的物理机制，我们还计算了在不同温度下波矢为 $k_z=0$ 、 $k_x=k_y=k$ 的声学支和光学支声子对热传导系数的贡献，如图3所示。图3中的曲线与图1中的色散关系曲线通过数字相对应。

由图3可见，在温度较低时，如低于60 K时，由于光学支频率高于声学支，而温度太低，其声子数会比声学支少很多，三根光频支曲线与横坐标轴基本重合，因此三个光学支对热膨胀几乎无贡献；而声学支1和2提供负热膨胀，声学支3提供正热膨胀，因此硅单晶呈现负热膨胀性质。当温度超过80 K时，

T = 20 K T = 60 K T = 80 K T = 200 K T = 400 K T = 800 K T = 1200 K T = 1600 K

Figure 3. Phonon contribution to heat conduction coefficient vs. ka/2 at different temperatures

图3. 不同温度下声子对热传导系数的贡献与ka/2之间的关系

光学支对热膨胀系数的贡献开始显现，其中光学支4、5提供正热膨胀系数，光学支6在全温度范围提供热膨胀系数几乎为0，并随温度继续升高，光学支提供的正热膨胀系数的增长追上并超过声学支提供的负热膨胀系数的增长，则总体上硅晶体的负热膨胀系数减小，并当温度超过120 K后呈现正热膨胀性质。在温度达到400 K后，各声学支提供的热膨胀系数随温度的升高而几乎不再增长，而，光学支4、5提供的正热膨胀系数也在增加，总的热膨胀系数为正，并随温度升高而增加；当温度达800 K以后，光学支4、5提供的正热膨胀系数随温度的升高几乎不再增加，因此硅单晶总体热膨胀系数随温度已不会有大的变化。

在文献中 [7]，我们基于目前被广泛使用的S-W模型研究硅单晶热膨胀性质，并没有得到硅单晶的低温负热膨胀系数的结果，这说明S-W模型存在问题。为了分析原因并找到硅单晶的低温负热膨胀性质的物理机制，我们用S-W模型计算了硅晶体中两体势 $U_2\left(r\right)$ 的三阶非和谐势能项 $g_1{\left(\text{Δ}r\right)}^3/6$ ，和三体势 $U_3\left(r_1,r_2,\theta \right)$ 的三阶非和谐势能项 $g_2\text{Δ}{r}_1{\left(\text{Δ}\theta \right)}^2/2$ ，其中 $g_1$ 、 $g_2$ 都为负值。由于在S-W模型中 $g_1$ 、 $g_2$ 都为负值，三阶非和谐势能随原子距离的增加而减小，贡献的是正热膨胀，因此我们提出了修正S-W模型的思路，即将 $g_2$ 由负值改为正值，并调整其大小，就能较好地计算出低温热膨胀系数，由于以前没有找到证据，我们的理论还是一种假设。

根据两体势和三体势函数，可以得到硅单晶中的力常数 $\alpha$ 和 $\beta$

$\alpha =-\frac{1}{3}\frac{{\partial }^2{U}_2\left(r\right)}{\partial r^2}-\frac{128}{9a^2}\frac{{\partial }^2{U}_3\left(r_1,r_2,\theta \right)}{\partial {\theta }^2}$ (6)

$\beta =-\frac{1}{3}\frac{{\partial }^2{U}_2\left(r\right)}{\partial r^2}+\frac{64}{9a^2}\frac{{\partial }^2{U}_3\left(r_1,r_2,\theta \right)}{\partial {\theta }^2}$ (7)

根据上式可知

$g_2=\frac{\partial }{\partial r_1}\frac{{\partial }^2{U}_3\left(r_1,r_2,\theta \right)}{\partial {\theta }^2}=-\frac{\sqrt{3}{a}^2}{32}\left({\alpha }^{\prime }-{\beta }^{\prime }\right)$ (8)

根据Rignanese [2] 等人根据第一性原理计算得到的数据，得到 ${\alpha }^{\prime }-{\beta }^{\prime }=-0.0638\text{h}/{\text{b}}^{\text{3}}$ ，因此由(8)可知， $g_2$ 为正，三体势贡献了负热膨胀系数热膨胀，至此找到了支持我们早先提出的低温下硅单晶的负热膨胀的物理机制的直接证据。

4. 结论

经过计算，本文得出以下结论。

1、在温度低于80 K，因此三个光学支对热膨胀几乎无贡献，而声学支总体上提供负热膨胀，因此硅单晶呈现负热膨胀性质；当温度超过80 K时，光学支对热膨胀系数的贡献开始显现，并总体上提供正热膨胀系数；随温度继续升高，光学支提供正热膨胀系数的增长追上并超过声学支提供的负热膨胀系数的增长，则总体上硅晶体的负热膨胀系数减小，并最终在约120 K温度下呈现正热膨胀性质；在温度达到400 K后，声学支总体上提供的负热膨胀系数随温度的升高而几乎不再变化，而光学支4、5提供的正热膨胀系数还在增加，总的热膨胀系数为正，并随温度升高而增加；当温度达800 K以后，光学支4、5提供的正热膨胀系数随温度的升高几乎不再增加，因此硅单晶总体热膨胀系数随温度已不会有大的变化。

2、根据Rignanese等人根据第一性原理计算得到的数据，得到三体相互作用势能的三阶力常数 $g_2$ ，即 ${\partial }^3{U}_3\left(r_1,r_2,\theta \right)/\partial r_1\partial {\theta }^2$ 为正，找到了支持我们早先提出的低温下硅单晶的负热膨胀的物理机制的直接证据。

NOTES

^*通讯作者。