1. 引言
振荡水翼在波浪能利用、潮流能利用和仿生推进等领域应用广泛,单个水翼和多个水翼的水动力性能均为基础科学问题,近年来受到学者的广泛关注。在理论研究方面,Lighthill [1] 用将鱼的尾鳍摆动简化建立了二维理论模型,并分析了尾鳍摇摆过程能够产生推力的流体动力学机理。随后,Wu [2] 在Lighthill的工作基础上考虑了波浪的影响,而Bose等 [3] 进一步研究了水翼振荡过程中吸收波浪能的机理。
在数值计算和实验方面,Read等 [4] 以振荡水翼为对象进行了流体动力特性试验研究,探究了振荡水翼水动力特性影响的关键参数。Peng等 [5] 通过数值仿真计算模拟了振荡水翼在有来流和水面波浪环境下吸收能量的能力。封培元 [6] 等在船体两侧构建了能够利用船体晃荡运动吸收能量的振荡水翼结构,并对水翼位置和浸没水深的影响进行了分析。王勇 [7] 等建立了一套通过双水翼振荡来吸收潮流能的系统,将动网格技术应用在流体域,计算了绕二维双水翼组合振荡流动的流动特性,研究了频率、振幅及雷诺数对潮流能吸收性能的影响。李键辉等 [8] 同样针对捕获潮流能的双水翼耦合振荡进行了水动力特性分析,研究表明当振荡频率较低时,水翼的边界易有涡脱落和边界层分离现象。马鹏磊 [9] 等提出了一种适用于垂直轴的振荡水翼发电系统,并建立了其摆动数学模型,分析了在不同运动参数下翼型的水动力性能。
多体类水翼结构也是多体船关注的方向之一,相关研究可作为多体组合水翼的参考。刘伟光 [10] 综合RANS方法、重叠网格技术、六自由度求解方法以及数值造波技术,建立了三体水翼复合船的运动预报及分析水翼系统减阻减摇的机理。刘胜 [11] 基于计算流体动力学分析软件对不同构型的三体船进行了静水阻力、静水航态、波浪总阻力、零航速横摇等水动力性能的计算研究。
上述研究中的多水翼组合分析主要是双体,本文针对三体组合摆动水翼的水动力特性进行分析,计算不同摆动角度和来流速度的影响,为多体水翼水动力学特性的研究提供参考。
2. 计算模型
2.1. 组合水翼计算模型
组合翼型采用二维模型计算水动力性能,来流方向由前缘向后缘方向,计算域设置速度入口和压力出口边界条件,计算翼型的摆动采用重叠网格,通过设置重叠域来实现翼型随时间的摆动。计算域的长度设置为1.8 m,其中速度入口距离前缘0.4 m,压力出口距离后缘为1.2 m,翼缘两侧距离边界为0.4 m。组合水翼几何模型及计算流体域如图1所示。
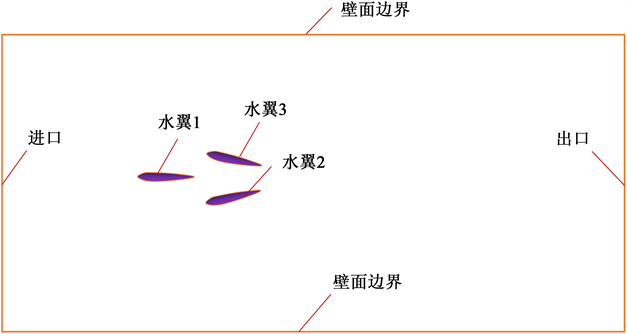
Figure 1. Computational domain and boundary conditions
图1. 计算域设置
2.2. 计算工况组设置
计算中,首先应用定常将某一速度工况下的流场计算稳定,然后应用非定常计算翼型以一定的旋转角速度进行摆动。其具体的计算工况如表1所示。

Table 1. Calculation condition setting
表1. 计算工况设置
翼型的摆动采用自定义函数,定义旋转速度为随着时间变化的分段函数,计算时间为4个摆动周期。流体介质为水,密度和动力粘度分别为997.561 kg/m3和0.00088 Pa.s。
3. 数值模拟
3.1. 控制方程
流体流动过程满足质量守恒定律、动量守恒定律和能量守恒定律三大守恒定律。动量守恒方程也称为N-S (Navier-Stokes)方程,其定义是控制流体的动量在时间上的变化率应该等于作用其上的力。表达式为:
在x方向:
(1)
在y方向:
(2)
在z方向:
(3)
式中,P为控制流体单元上作用的压力,τxx、τxy和τxz分别是粘性力τ在三个方向上的分量,fx、fy和fz为考虑微元体上作用的其他力,V是速度矢量。
根据质量守恒定律,控制体流入的质量与流出质量之差值需要等于它内部质量的增量。表达式为:
(4)
式中,t为时间,为控制体的密度,u、v、w分别是控制体流动速度矢量在x、y、z方向上分量。
由于湍流流动过程复杂,现有的湍流数值计算中,需要根据计算精度和具备的计算资源选择较合适的湍流模型。湍流流动常见的模拟方法有直接数值模拟、大涡模拟和雷诺平均方法。直接数值模拟方法理论上不用对湍流流动进行简化和假设,可从理论上得到精确结果,但对计算机资源要求较高。大涡模拟法直接对大尺度涡进行求解,然后对小尺度下的涡采用模型求解。相较于直接数值模拟法效率要高,但仍然需要大量计算。雷诺平均法更加符合工程中的应用,k-ε模型提出后逐渐成为计算流体动力学中最广泛应用的模型,其精度在工程可接受范围内同时计算速度较快。RNG k-ε湍流模型在k-ε模型的基础上进行了改进,进一步提升了计算的准确性。本文使用的SST k-ω模型是在k-ε模型和k-ω模型的基础上改进得到的,该模型使得k-ε模型在近壁面流动时也能够有较好的准确性。
3.2. 网格划分
网格主要分为背景网格和重叠网格两部分,重叠网格位于背景网格之内,计算中背景网格在重叠网格的区域进行挖洞处理,重叠网格边界会和背景网格进行插值计算,实现背景网格和重叠网格之间的流场信息交换,因此重叠网格对大幅运动的流场求解具有很大的优势,从而避免了物体大幅运动而产生的网格变形。
网格全局尺寸设置为0.01 m;翼型表面网格设置为0.002 m,并设置边界层数为5层,第一层边界层网格厚度为0.5 mm;对重叠网格区域进行两个阶梯性加密,其网格尺寸分别为2 mm和4 mm。网格如图2所示。
背景网格中对重叠网格区域进行加密,其分为两个不同尺寸的加密区域,由重叠网格区域向外尺寸变大,重叠网格域的尺寸为2 mm,并对翼型设置了5层边界层。
4. 计算结果及分析
4.1. 不同摆动角度下组合水翼水动力特性研究
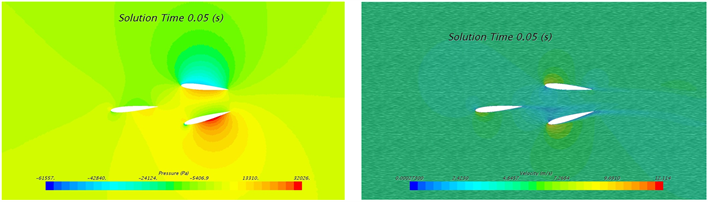
分别计算摆动角速度为100˚/s和摆动角度为±5˚、±10˚、±20˚的工况。摆动角度为±5˚时4个典型位置的压力云图如图3左侧图示,其中t = 0.05 s时刻为+5˚摆动角,且向中间位置摆动,其迎面(下侧)处产生较高压力,背面(上侧)产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−61557 Pa;t = 0.15 s时刻为−5˚摆动角,且向中间位置摆动,其迎面(上侧)产生较高压力,背面(下侧)处产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−58462 Pa;t = 0.1 s时刻,翼型位移摆动角为0˚的中间位置,高低压区域主要分布在翼型2和翼型3表面,且在两翼型夹角内侧产生高压,前缘外侧产生低压。分析认为压力分布主要是由于t = 0.05 s时刻翼型2与来流攻角较大,t = 0.15 s时刻翼型3与来流攻角较大,在叶背区域形成流动分离,从而产生了较大的压强。
 (a) t = 0.05 s
(a) t = 0.05 s  (b) t = 0.1 s
(b) t = 0.1 s 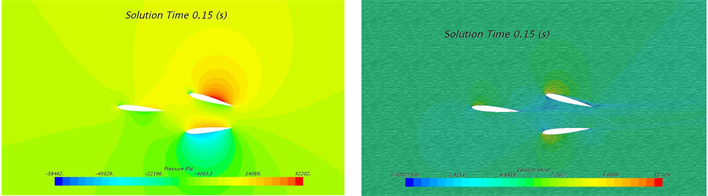 (c) t = 0.15 s
(c) t = 0.15 s
Figure 3. Contour of pressure and velocity at 5˚ swing: (a) 0.05 s; (b) 0.1 s; (c) 0.15 s
图3. 水翼5˚摆角下不同时刻压力与速度云图:(a) 0.05 s; (b) 0.1 s; (c) 0.15 s
摆动角度为±5˚时4个典型位置的速度云图如图3右侧图示,其中t = 0.05s时刻为+5˚摆动角,且向中间位置摆动,在翼型2和翼型3夹角外侧靠近前缘处产生较高流速,且迎面(下侧)高流速区域大于背面,最大流速为12.1 m/s;t = 0.15 s时刻为−5˚摆动角,且向中间位置摆动,在翼型2和翼型3夹角外侧靠近前缘处产生较高流速,且迎面(上侧)高流速区域大于背面,最大流速为12.1 m/s;t = 0.1 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生高流速区域,根据各自的摆动情况,迎面的高流速区域大于背面,其最大流速分别为11.7 m/s和11.6 m/s;不同时刻,高流速分布区域始终位于翼型2和翼型3前缘区域。
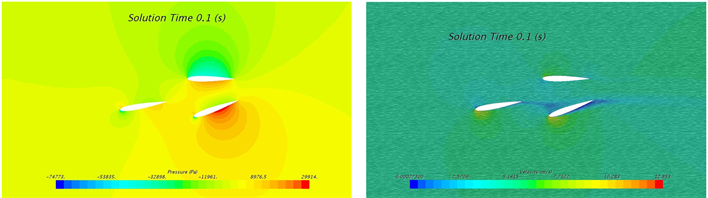
摆动角度为±10˚时4个典型位置的压力云图和速度云图如图4所示,其中t = 0.1 s时刻为+10˚摆动角,且向中间位置摆动,其迎面(下侧)处产生较高压力,背面(上侧)产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−74773 Pa;t = 0.3 s时刻为−10˚摆动角,且向中间位置摆动,其迎面(上侧)产生较高压力,背面(下侧)处产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−71986 Pa;t = 0.2 s时刻,翼型位移摆动角为0˚的中间位置,高低压区域主要分布在翼型2和翼型3表面,且在两翼型夹角内侧产生高压,前缘外侧产生低压。
 (a) t = 0.1 s
(a) t = 0.1 s  (b) t = 0.2 s
(b) t = 0.2 s 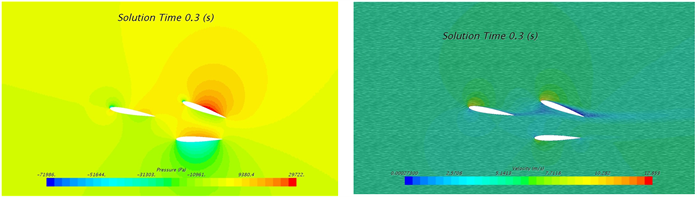 (c) t = 0.3 s
(c) t = 0.3 s
Figure 4. Contour of pressure and velocity at 10˚ swing: (a) 0.1 s; (b) 0.2 s; (c) 0.3 s
图4. 水翼10˚摆角下不同时刻压力与速度云图:(a) 0.1 s; (b) 0.2 s; (c) 0.3 s
摆动角度为±10˚时4个典型位置的速度云图如图4右侧图示,其中t = 0.1 s时刻为+10˚摆动角,且向中间位置摆动,在翼型2和翼型3夹角外侧靠近前缘处产生较高流速,且迎面(下侧)高流速区域大于背面,最大流速为12.9 m/s;t = 0.3 s时刻为−10˚摆动角,且向中间位置摆动,在翼型2和翼型3夹角外侧靠近前缘处产生较高流速,且迎面(上侧)高流速区域大于背面,最大流速为12.9 m/s;t = 0.2 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生高流速区域,根据各自的摆动情况,迎面的高流速区域大于背面,其最大流速分别为11.43 m/s和11.39 m/s;不同时刻,高流速分布区域始终位于翼型2和翼型3前缘区域。
摆动角度为±20˚时4个典型位置的压力云图和速度云图如图5所示,其中t = 0.2 s时刻为+20˚摆动角,且向中间位置摆动,其迎面(下侧)处产生较高压力,背面(上侧)产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−114900 Pa;t = 0.6 s时刻为−10˚摆动角,且向中间位置摆动,其迎面(上侧)产生较高压力,背面(下侧)处产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−104800 Pa;t = 0.4 s时刻,翼型位移摆动角为0˚的中间位置,高低压区域主要分布在翼型2和翼型3表面,且在两翼型夹角内侧产生高压,前缘外侧产生低压。
 (a) t = 0.2 s
(a) t = 0.2 s  (b) t = 0.4 s
(b) t = 0.4 s 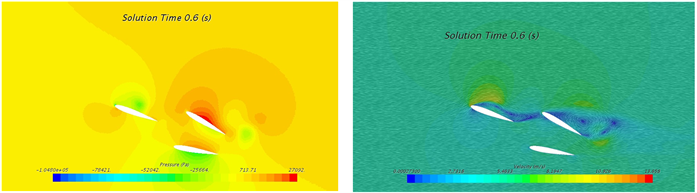 (c) t = 0.6 s
(c) t = 0.6 s
Figure 5. Contour of pressure and velocity at 20˚ swing: (a) 0.2 s; (b) 0.4 s; (c) 0.6 s
图5. 水翼20˚摆角下不同时刻压力与速度云图:(a) 0.2 s; (b) 0.4 s; (c) 0.6 s
摆动角度为±20˚时4个典型位置的速度云图如图5右侧图示,其中t = 0.2 s时刻为+20˚摆动角,且向中间位置摆动,在翼型1迎面(下侧)靠近前缘处产生较高流速,最大流速为14.2 m/s;t = 0.6 s时刻为−20˚摆动角,且向中间位置摆动,在翼型1迎面(上侧)靠近前缘处产生较高流速,最大流速为13.7 m/s;t = 0.4 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生高流速区域,根据各自的摆动情况,迎面的高流速区域大于背面,其最大流速分别为12.0 m/s和11. 9 m/s。
对比不同摆动角度下三体组合振荡水翼的最大流速区域可以看到,在摆动角度为±20˚时与小角度摆动时区域不一样,这主要是由于大角度摆动时翼型1的尾流对翼型2和3的进流产生了扰动,而小角度摆动时,翼型1的尾流主要影响范围尚未到达翼型2和翼型3的首部区域。
4.2. 不同来流速度下组合水翼水动力特性研究
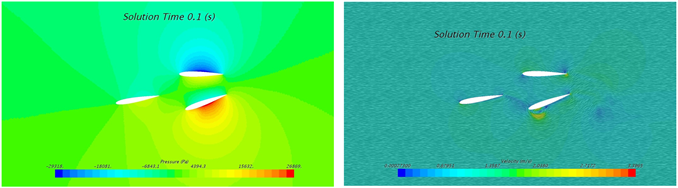
来流速度为1 m/s时4个典型位置的压力云图和速度云图如图6所示,其中t = 0.1 s时刻为+10˚摆动角,且向中间位置摆动,其迎面(下侧)处产生较高压力,背面(上侧)产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−29318 Pa;t = 0.3 s时刻为−10˚摆动角,且向中间位置摆动,其迎面(上侧)产生较高压力,背面(下侧)处产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−28923 Pa;t = 0.2 s时刻,翼型位移摆动角为0˚的中间位置,高低压区域主要分布在翼型2和翼型3表面,且在两翼型夹角内侧产生高压,前缘外侧产生低压。
来流速度为1 m/s时4个典型位置的速度云图如图6右侧图示,其中t = 0.1 s时刻为+10˚摆动角,且向中间位置摆动,其迎面(下侧)靠近前缘部位产生较大速度,最大速度为1.70 m/s;t = 0.3 s时刻为−10˚摆动角,且向中间位置摆动,其迎面(上侧)靠近前缘部位产生较大速度,最大速度为1.64 m/s;t = 0.2 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生高流速区域,根据各自的摆动情况,迎面的高流速区域大于背面,其最大流速分别为1.22 m/s和1.24 m/s;不同时刻,其最小流速始终分布在翼型前缘,且在后缘产生尾涡。
 (a) t = 0.1 s
(a) t = 0.1 s 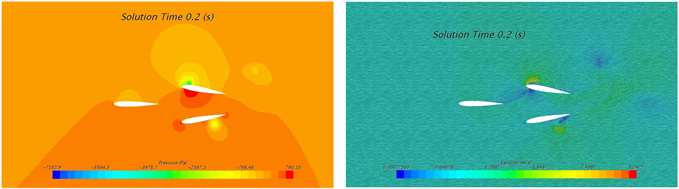 (b) t = 0.2 s
(b) t = 0.2 s  (c) t = 0.3 s
(c) t = 0.3 s
Figure 6. Contour of pressure and velocity at inlet velocity of 1 m/s: (a) 0.1 s; (b) 0.2 s; (c) 0.3 s
图6. 来流速度1 m/s时不同时刻压力与速度云图:(a) 0.1 s; (b) 0.2 s; (c) 0.3 s
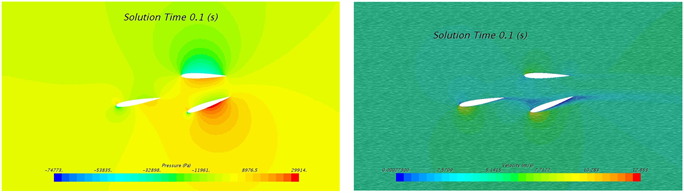
来流速度为5 m/s时4个典型位置的压力云图和速度云图如图7所示,其中t = 0.1 s时刻为+10˚摆动角,且向中间位置摆动,其迎面(下侧)处产生较高压力,背面(上侧)产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−74773 Pa;t = 0.3 s时刻为−10˚摆动角,且向中间位置摆动,其迎面(上侧)产生较高压力,背面(下侧)处产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−71986 Pa;t = 0.2 s时刻,翼型位移摆动角为0˚的中间位置,高低压区域主要分布在翼型2和翼型3表面,且在两翼型夹角内侧产生高压,前缘外侧产生低压。
来流速度为5 m/s时4个典型位置的速度云图如图7右侧图示,其中t = 0.1 s时刻为+10˚摆动角,且向中间位置摆动,在翼型2和翼型3夹角外侧靠近前缘处产生较高流速,且迎面(下侧)高流速区域大于背面,最大流速为12.9 m/s;t = 0.3 s时刻为−10˚摆动角,且向中间位置摆动,在翼型2和翼型3夹角外侧靠近前缘处产生较高流速,且迎面(上侧)高流速区域大于背面,最大流速为12.9 m/s;t = 0.2 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生高流速区域,根据各自的摆动情况,迎面的高流速区域大于背面,其最大流速分别为11.43 m/s和11.39 m/s;不同时刻,高流速分布区域始终位于翼型2和翼型3前缘区域。
 (a) t = 0.1 s
(a) t = 0.1 s  (b) t = 0.2 s
(b) t = 0.2 s 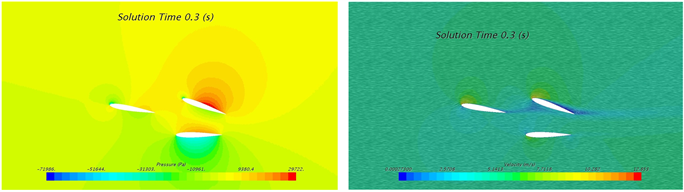 (c) t = 0.3 s
(c) t = 0.3 s
Figure 7. Contour of pressure and velocity at inlet velocity of 5 m/s: (a) 0.1 s; (b) 0.2 s; (c) 0.3 s
图7. 来流速度5 m/s时不同时刻压力与速度云图:(a) 0.1 s; (b) 0.2 s; (c) 0.3 s
来流速度为10 m/s时4个典型位置的压力云图和速度云图如图8图示,其中t = 0.1 s时刻为+10˚摆动角,且向中间位置摆动,其迎面(下侧)处产生较高压力,背面(上侧)产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−348750 Pa;t = 0.3 s时刻为−10˚摆动角,且向中间位置摆动,其迎面(上侧)产生较高压力,背面(下侧)处产生较低压力,高低压区域主要分布在翼型2和翼型3表面,最低压为−346190 Pa;t = 0.2 s时刻,翼型位移摆动角为0˚的中间位置,高低压区域主要分布在翼型2和翼型3表面,且在两翼型夹角内侧产生高压,前缘外侧产生低压。
来流速度为10 m/s时4个典型位置的速度云图如图8右侧图示,其中t = 0.1 s时刻为+10˚摆动角,且向中间位置摆动,在翼型2和翼型3夹角外侧靠近前缘处产生较高流速,且迎面(下侧)高流速区域大于背面,最大流速为26.6 m/s;t = 0.3 s时刻为−10˚摆动角,且向中间位置摆动,在翼型2和翼型3夹角外侧靠近前缘处产生较高流速,且迎面(上侧)高流速区域大于背面,最大流速为26.5 m/s;t = 0.2 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生高流速区域,根据各自的摆动情况,迎面的高流速区域大于背面,其最大流速分别为21.9 m/s和21.8 m/s。
 (a) t = 0.1 s
(a) t = 0.1 s  (b) t = 0.2 s
(b) t = 0.2 s  (c) t = 0.3 s
(c) t = 0.3 s
Figure 8. Contour of pressure and velocity at inlet velocity of 10 m/s: (a) 0.1 s; (b) 0.2 s; (c) 0.3 s
图8. 来流速度10 m/s时不同时刻压力与速度云图:(a) 0.1 s; (b) 0.2 s; (c) 0.3 s
4.3. 组合水翼受力结果
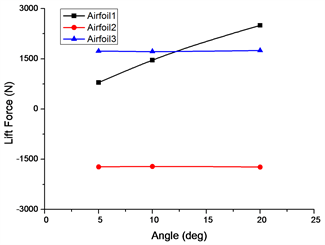
根据计算结果提取不同摆动角度和速度下的最大升力和阻力曲线,如图9和图10所示。
 (a) 升力
(a) 升力 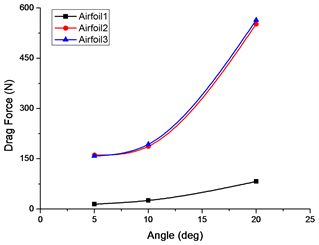 (b) 阻力
(b) 阻力
Figure 9. Lift and drag force under different swing angles
图9. 不同摆动角度下的升力和阻力
由图9可知,在不同摆动角度工况下,随着摆动角度的增大,阻力增加,且增加的速度也在增大;随着摆动角度的增加,翼型2和翼型3的升力变化不大,翼型1的升力逐渐增大。翼型2和翼型3升力呈对称分布,说明在这种低速摆动运动过程中对称角度上流场基本呈对称性,使得作用在两个翼型上升力相同。
 (a) 升力
(a) 升力 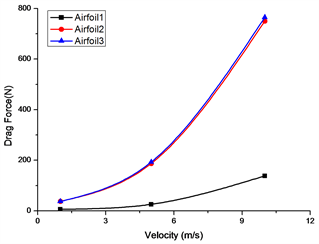 (b) 阻力
(b) 阻力
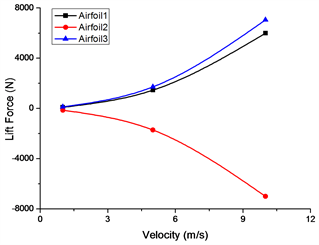
Figure 10. Lift and drag force at different incoming flow velocity
图10. 不同来流速度下的升力和阻力
由图10可以看到,在不同来流速度工况下,随着速度的增大,左右翼型的升力和阻力均增大,且升力和阻力增加的速度逐渐增大。不同流速下翼型2和翼型3的阻力随来流速度快速增加,而翼型1增长较慢,表明本文中分布的三体水翼的整体阻力主要发生在后两个翼型上,其受来流速度影响较大。
5. 结论
通过对组合翼型不同摆动角度和来流速度下的流场进行计算,得到以下结论:
1) 在不同摆动角度工况下,压力分布和速度分布相互对应,流速较大的区域为低压区域,高、低压区域和高、低流速区域分布大致相同,且高低压和高流速区域主要分布在两个尾部翼型附近区域。随着摆动角度的增大,最大压力变化较小,最低压力(负压)逐渐增大。
2) 在不同来流速度工况下,压力分布和速度分布相互对应,流速较大的区域为低压区域,高、低压区域和高、低流速区域分布大致相同,且高低压和高流速区域主要分布在两个尾部翼型附近区域。随着来流速度的增大,最大压力和最小压力(负压)均均有不同程度的增大。
3) 通过对不同工况的升力和阻力曲线分析,随着摆动角度的增大阻力均增大,阻力增加的速度逐渐增大;随着摆动角度的增大,尾部翼型的升力变化较小,两翼型升力方向相反,首部翼型随着摆动角度的增大,其升力逐渐增大;随着来流速度的增大,所有翼型的升力和阻力增大,且增大的速度逐渐增大。
基金项目
装备预研领域基金项目资助(No.61402070503);武汉理工大学国家级大学生创新创业训练计划资助(No.20191049702018);中央高校基本科研业务费专项资金资助(No.2019IVA076)。
NOTES
*通讯作者。