谐振泵浦2640 nm Ho:YAG/SrWO₄中红外拉曼激光器理论研究

Theoretical Study of Resonantly Pumped Mid-Infrared Ho:YAG/SrWO₄ Intracavity Raman Laserat 2640 nm

摘要: 根据谐振泵浦Ho:YAG激光器的能量传递过程，构建了Ho:YAG/SrWO₄主动调Q拉曼激光器的准二能级速率方程模型。数值模拟得到了晶体内反转粒子数密度、腔内基频光子数密度和拉曼光子数密度随时间的变化关系，并利用该模型分析了Q开关重复频率和输出镜透过率大小等因素对激光器输出的平均输出功率、脉冲宽度、单脉冲能量和峰值功率的影响。为后续实验获得稳定高效的2640 nm拉曼激光输出奠定了理论基础。

Abstract: The theoretical model of quasi-two-level Ho:YAG/SrWO₄ actively Q-switched Raman laser is established according to the energy transfer process of Hoion in a resonantly pumped Ho:YAG laser. The relationship between the inverted particle density in the laser crystal, the density of the funda-mental photon and the Raman photon with time is obtained by numerical simulation. The influences of Q-switch frequency and output mirror transmittance on the average output power, pulse width, pulse energy, and peak power of the Raman laser are also analyzed, which provides a theoretical basis for achieving stable and high efficient Raman laser output at 2640 nm in future experiment investigation.

1. 引言

2 μm波段处于三个传输损耗较低的大气窗口之一，具有人眼安全特性，且可以作为3-12μm光学参量振荡器的理想泵浦源 [1]，因此其具有广阔的应用前景。作为该激光器的基频光增益介质，Ho:YAG晶体因其较大的发射截面和较长的上能级寿命，在2 μm中红外波段激光器的研究中备受关注 [2] [3]。同时，Ho³⁺掺杂材料具有量子缺陷较低、上转换损耗较低等优点，也为Ho:YAG固体激光器的稳定高效运转奠定了基础 [4]。随着高质量晶体的发展，在现有的拉曼晶体中，SrWO₄因其高拉曼增益系数、高光学损伤阈值、良好的机械性能和热性能等优点在近红外波段内得到了广泛的研究 [5] [6] [7]。2 μm波段激光在激光医疗、化学传感、激光测距和环境监测等领域都有非常重要的应用 [8] [9]，但目前2 μm波段基于SrWO₄晶体的拉曼激光器鲜有报道。

由于拉曼晶体的拉曼增益系数几乎与泵浦光的波长成反比，波长越长，越难以实现高效的拉曼转换 [10]。因此，如何实现高效的拉曼输出，成为目前中红外波段拉曼激光器研究的关键问题。为了提高拉曼转换效率，实现稳定高效的拉曼光输出，需要构建激光器的理论模型，对激光器的参数进行研究。丁双红等人曾对近红外波段主动调Q拉曼激光器的速率方程进行了详细的研究 [11] [12]。然而，该模型并未考虑脉冲重频变化对激光器的影响，默认激光器在高重频下运转，不适用于低重频情形。此外，Nd³⁺掺杂材料一般为四能级系统，运转过程与Ho³⁺掺杂材料的准二能级系统存在较大差异。朱国利曾对Ho:YAG激光器进行了理论研究，分析了Ho:YAG主动调Q脉冲激光器的运转过程，并给出了高重频下Ho:YAG激光器的速率方程模型 [13]；段小明也曾基于Ho:YAG的能量传递过程，给出了Ho:YAG激光器准二能级系统的稳态速率方程 [14]。尽管目前已有数篇对2 μm波段拉曼激光器实验研究的报道 [10] [15] [16]，但据我们了解，对Ho:YAG/SrWO₄拉曼激光器的理论研究还未见报道。

本文根据谐振泵浦Ho:YAG激光器的能量传递过程，考虑自发辐射的影响，在平面波近似下构建了Ho:YAG/SrWO₄主动调Q拉曼激光器的准二能级速率方程模型。明确给出了激光器运转过程中反转粒子数密度、腔内基频光子数密度和拉曼光子数密度随时间的变化表达式，并利用该模型分析了Q开关重复频率和输出镜透过率等因素对激光器的平均输出功率、脉冲宽度、单脉冲能量和峰值功率的影响，为后续实验获得稳定高效的2640 nm拉曼激光输出奠定了理论基础。

2. Ho:YAG/SrWO₄拉曼激光器速率方程模型的建立

2.1. Ho:YAG激光器的运转机制

1908 nm激光泵浦的Ho:YAG激光器在常温运转过程中可以视作是准二能级激光系统。在基质晶体场的作用下，Ho:YAG中掺杂的Ho³⁺会发生Stark能级分裂，形成多重态Stark能级 [14]。Ho:YAG激光器的运转机制如图1所示，基态能级⁵I₈上的Ho³⁺吸收1908 nm的泵浦光跃迁到激发态的Stark能级，当实现粒子数反转后，激发态能级⁵I₇上的Ho³⁺向基态Stark能级跃迁并发出2122 nm激光。由于泵浦终态能级就是激光的上能级，而激光的终态能级正位于基态能级上，因此整个系统在运转过程中量子亏损极小，激光器可以高效运行。

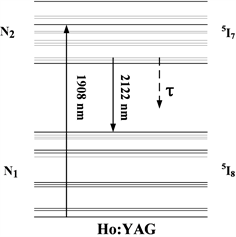
Figure 1. Diagram of energy level transition process about Ho:YAG crystalinoperation process about Ho:YAG Laser

图1. Ho:YAG激光器运转过程中的能级跃迁示意图

2.2. Ho:YAG/SrWO₄拉曼激光器速率方程

数值模拟基于的实验装置如图2所示，Ho:YAG/SrWO₄拉曼激光器采用线性耦合腔设计。基频光谐振腔由M1镜和M3镜组成，腔长为170 mm。M2镜和M3镜组成拉曼光谐振腔，腔长为50 mm。平面输入镜M1上镀有1908 nm处高透(T > 99.5%)，2122 nm处高反(R > 99.8%)的膜。曲率半径为259 mm的平凹镜M3上镀有2122 nm处高反(R > 99.5%)，2640 nm处部分反射的膜，同时，它也起到拉曼激光器输出镜的作用。拉曼中间镜M2的一侧镜面上镀有2122 nm处高透(R < 1%)的膜，另一侧镜面上镀有2122 nm处高透(R < 1%)的膜和2640 nm处高反(R > 99.8%)的膜。

Figure 2. Diagram ofexperimentalsetup

图2. 实验装置示意图

结合如图2所示的准二能级系统的运转过程示意图，有Ho:YAG准二能级系统连续运转时的速率方程如下 [14]：

$N_{\text{Ho}}=N_1+N_2$ (1)

$\Delta N=f_u{N}_2-f_l{N}_1$ (2)

$\frac{\text{d}{N}_1}{\text{d}t}=\frac{\text{d}{N}_{\text{Ho}}}{\text{d}t}-\frac{\text{d}{N}_{\text{2}}}{\text{d}t}=-\frac{\text{d}{N}_2}{\text{d}t}$ (3)

$\frac{\text{d}{N}_2}{\text{d}t}=R-\frac{c\sigma }{n}\Delta N{\Phi }_L-\frac{N_2-N_2^0}{\tau }$ (4)

式中，N₁和N₂分别表示的分别为⁵I₈和⁵I₇能级的粒子数密度，N_Ho为激光晶体中Ho³⁺的总密度，ΔN为谐振腔内反转粒子数密度，f_u、f_l分别为⁵I₇和⁵I₈能级的玻尔兹曼因子，R为泵浦速率，c为真空光速，σ为Ho³⁺的受激发射截面，n为激光晶体的折射率，Ф_L为腔内光子总数，τ为激光上能级的自发辐射寿命， $N_2^0$ 为未泵浦时的上能级粒子数密度，ΔN⁰为初始的反转粒子数密度。

考虑到主动调Q脉冲激光器中脉冲产生的过程为瞬态过程，脉冲建立期间受激辐射现象对腔内光子数和反转粒子数的影响要比其它因素大得多，可以忽略式中的泵浦项来简化计算过程，得到主动调Q脉冲激光器的速率方程：

$\frac{\text{d}{\Phi }_L}{\text{d}t}=\frac{c}{2L_r}\cdot \text{2}\sigma \Delta N{\Phi }_L{n}_L{l}_L-\frac{{\Phi }_L}{t_L}$ (5)

$\frac{\text{d}\Delta N}{\text{d}t}=-\left(1+f_l/f_u\right)c\sigma \Delta N{\Phi }_L-\frac{\Delta N}{\tau }$ (6)

式中，n_L为激光增益介质的折射率， $t_L=2L_r/c\left[L-\ln \left(R_{1L}{R}_{2L}\right)\right]$ 为基频光的光子寿命，L_r为基频光谐振腔的光学长度，L为谐振腔固有损耗。

向Ho:YAG脉冲激光器的速率方程中引入描述受激拉曼散射过程的项，记反转因子 $\gamma =1+f_l/f_u$，定义拉曼增益 $G=2gh{\nu }_{S}c{n}_S{l}_S$，整理得到Ho:YAG/SrWO₄主动调Q拉曼激光器速率方程：

$\frac{\text{d}\Delta N}{\text{d}t}=-\gamma c\sigma \Delta N{\Phi }_L-\frac{\Delta N}{\tau }$ (7)

$\frac{\text{d}{\Phi }_L}{\text{d}t}=\frac{c}{2L_r}\cdot 2\sigma \Delta N{\Phi }_L{n}_L{l}_L-\frac{c}{2L_S}G{\Phi }_L{\Phi }_S-\frac{{\Phi }_L}{t_L}$ (8)

$\frac{\text{d}{\Phi }_S}{\text{d}t}=\frac{c}{2L_S}G{\Phi }_L{\Phi }_S-\frac{{\Phi }_S}{t_S}$ (9)

式中， $t_S=2L_S/c\left[L-\ln \left(R_{1S}{R}_{2S}\right)\right]$ 为拉曼光的光子寿命，L_S为拉曼光谐振腔的光学长度，l_L为激光晶体长度，l_S为拉曼晶体长度，n_S为拉曼晶体的折射率，g为拉曼晶体的拉曼增益系数，h为普朗克常数，ν_S为拉曼光的光频率，Ф_S为腔内拉曼光光子数密度。

对于主动调Q脉冲激光器，在脉冲建立之前，腔内的反转粒子数的密度主要取决于泵浦光的功率和Q开关重复频率等因素，因此有t = 0时刻，初始反转粒子数密度ΔN⁰ [17]

$\Delta N^0=\left(f_u+f_l\right)R\tau \left[1-\exp \left(-\frac{1}{f_p\tau }\right)\right]-f_l{N}_{\text{Ho}}$ (10)

式中，f_p为Q开关的重复频率，泵浦速率R

$R=\frac{P_{in}{\eta }_{\alpha }{\eta }_p}{\pi {\omega }_p^2{l}_{L}h{\nu }_p}$ (11)

式中， $P_{in}$ 为泵浦功率， ${\eta }_{\alpha }=\left[1-\exp \left(-\alpha l_L\right)\right]$ 为激光增益介质对泵浦光的吸收效率， $\alpha$ 为激光增益介质的吸收系数， ${\eta }_p$ 为泵浦光的量子效率,ν_P为泵浦光的光频率。

为了更好地描述激光器的输出特性，需要对激光器运转过程中的平均输出功率、脉冲宽度、单脉冲能量和峰值功率做进一步的数值模拟。根据Degnan关于脉冲激光器理论研究的报道，可以得到峰值功率的解析表达式 [18]：

$P_{peak}=\frac{1}{2t_S}h{\nu }_S\pi {\omega }_S^2{l}_S{\eta }_c\cdot {\Phi }_{S\text{\_}\max }$ (12)

式中， ${\Phi }_{S\text{\_}\max }$ 为腔内拉曼光子数密度最大值， ${\eta }_c$ 为激光器输出时的耦合效率 [19]，有

${\eta }_c=\frac{T}{T+\delta }$ (13)

式中，T为输出镜透过率， $\delta =L-\ln \left(R_{1S}{R}_{2S}\right)$ 为激光器谐振腔的总损耗。

查阅相关文献，给出此次速率方程模型计算时所需使用的参数如表1所示。根据下表中的参数，对激光器的输出特性进行模拟。

Table 1. Rate equation’s model parameters of Ho: YAG/SrWO4Raman Laser

表1. Ho:YAG/SrWO₄拉曼激光器速率方程模型参数

3. 仿真结果与分析

通过对速率方程式(7)、(8)和(9)数值求解，可以得到脉冲建立过程中晶体内反转粒子数密度、腔内基频光子数密度和拉曼光子数密度随时间变化的关系图，如图3所示。

如图3(a)所示，是在脉冲建立过程中，晶体内反转粒子数密度的变化情况。t = 0时刻，Q值突变，上能级的反转粒子开始向下能级跃迁，基频光光子迅速增加，形成基频光脉冲；随着基频光光子数密度的增加，当达到拉曼阈值时，受激拉曼散射现象发生，继而产生拉曼光脉冲，如图3(b)所示。

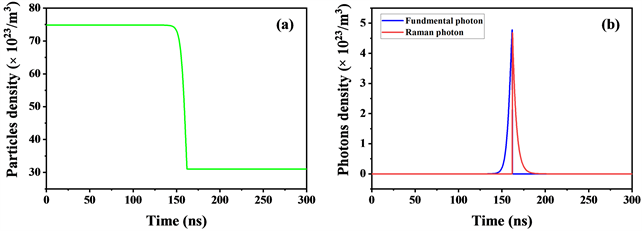
Figure 3. (a) Populationinversion density and (b) fundamental photon density and Raman photondensity

图3. (a) 反转粒子数密度和(b) 基频光子数密度和拉曼光子数密度

3.1. Q开关重复频率对激光器输出特性的影响

根据Degnan关于脉冲激光器理论研究的报道 [16]，对于主动调Q激光器速率方程模型，Q开关重复频率的变化会对初始反转粒子数的大小直接产生影响。结合表1中给出的参数，可以得到脉冲重频分别在4 kHz、7 kHz和10 kHz下激光器的平均输出功率、脉冲宽度、单脉冲能量和峰值功率随泵浦功率的变化情况，所得结果如图4所示。

Figure 4. The changing of (a) peak power, (b) pulse width, (c) pulse energy and (d) average output power with pump power under different Q-switch frequencies

图4. 不同脉冲重频下(a) 峰值功，(b) 脉冲宽度，(c) 单脉冲能量，及(d) 平均功率随泵浦功率变化趋势

对比图4(a)和图4(c)可以发现，随着Q开关重复频率的增加，激光器输出的峰值功率和单脉冲能量出现了明显的下降，究其原因在于随重频的增加，腔内功率密度下降。从图4(b)中可以看出，在泵浦功率刚超过拉曼阈值时，脉冲宽度会随着泵浦功率的增加而迅速降低；但随着泵浦功率不断增加，激光器出现饱和现象，图中表现为脉冲宽度的下降幅度减小，并最终稳定在一个值附近。此外，观察图4(d)中4 kHz和7 kHz的曲线可以发现，在泵浦功率较低时，4 kHz下激光器的平均输出功率明显更高；但随着泵浦功率的增加，二者曲线出现交点，最终在7 kHz的脉冲重频下可以取得更高的输出功率。

为了进一步探究脉冲重频对激光器输出特性的影响，这里分别取泵浦功率为5 W、10 W和15 W，在1 kHz到10 kHz范围内改变Q开关重复频率，得到激光器的平均输出功率、脉冲宽度、单脉冲能量和峰值功率随脉冲重频的变化情况，模拟结果如图5所示。

Figure 5. The changing of (a) peak power, (b) pulse width, (c) pulse energy and (d) average output power with Q-switch frequency under different pump powers

图5. 不同脉冲重频下(a) 峰值功，(b) 脉冲宽度，(c) 单脉冲能量，及(d) 平均功率随泵浦功率变化趋势

从图5(a)~(c)中可以看出，在5 W、10 W和15 W的泵浦功率下，随着脉冲重频的增加，激光器输出的峰值功率与单脉冲能量均呈现下降趋势；脉冲宽度会随重频增加而增加，但在5 W的低泵浦功率下，脉宽的增长趋势更为明显。图5(d)是激光器的平均输出功率随重频的变化情况，可以看出，在不同的泵浦功率下，其对应的最佳重频并不相同。5 W和10 W泵浦功率下，取得最大平均输出功率时对应的最佳重频分别为2 kHz和4 kHz；而泵浦功率为15 W时，在4 kHz到7 kHz范围内，激光器的平均输出功率均处于较高的水平。

结合以上模拟结果，考虑到调Q模式下激光器谐振腔内的功率密度较高，为保证激光器长期稳定运行，防止光学元件损坏，需要对腔内功率密度进行控制。结合上述模拟情况，在低泵浦功率下，适当减小Q开关的重复频率，可以提高腔内功率密度，降低拉曼阈值；而当泵浦功率较高时，需要适当增大Q开关的重复频率，以减小腔内功率密度，延缓激光器饱和现象出现，从而能更好地利用泵浦源能量，最终获得更稳定更高效的激光输出。

3.2. 输出镜透过率的变化对激光器输出特性的影响

分析激光器的运转过程可以发现，输出镜的透过率会影响初始反转粒子数密度和激光器输出时的耦合效率，对激光器的峰值功率、脉冲宽度、单脉冲能量和平均输出功率等都会产生影响，是谐振腔设计中必须考虑的重要参数。结合速率方程和表1中给出的参数，取脉冲重频为4 kHz，泵浦功率为5 W，可以得到不同输出镜透过率下激光器峰值功率、脉冲宽度、单脉冲能量和平均输出功率，如图6所示。

Figure 6. The changing of output characteristics under different transmittance from of output mirror: (a) pulse width, (b) average output power, (c) peak power, and (d) pulse energy

图6. 不同输出镜透过率下(a) 峰值功率，(b) 单脉冲能量，(c) 脉冲宽度，及(d) 平均输出功率的变化情况

可以看到，输出镜透过率为60%时，激光器输出的峰值功率最高；在50%的输出镜透过率处，单脉冲能量最大；在30%到60%的范围内，激光器输出的平均功率均处于一个较高的水平；当透过率超过60%时，激光器的平均输出功率会出现明显下降。

4. 结论

至此，我们研究了Q开关重复频率和输出镜透过率对激光器输出特性的影响，并实现了参数优化。根据上述的模拟结果可以发现，当泵浦功率较低时，降低重频和减小透过率有助于拉曼光的建立，较低的泵浦功率下就可以得到稳定的拉曼输出；但随着泵浦功率的增加，过高的腔内能量密度会影响激光器的输出进一步提高，需要在一定范围内增大脉冲重频或输出镜透过率，以减小腔内的能量密度，延缓饱和现象的出现，最终获得更高的输出功率和脉冲能量。

本文从Ho:YAG晶体的能量传输机制出发，构建了考虑自发辐射跃迁的影响的Ho:YAG/SrWO₄主动调Q拉曼激光器的速率方程模型。通过数值求解得到了激光器瞬态运转情况，并研究了主动调Q脉冲重频和输出镜透过率对激光器输出特性的影响，实现对激光器参数的优化。对于Ho:YAG/SrWO₄拉曼激光器，在现有的实验条件下，最佳的脉冲重频在4~7 kHz之间，最佳的输出镜透过率在50%~60%之间，所得的理论结果为后续的实验研究具有重要的指导意义。

基金项目

国家自然科学基金(61775166, 61275138)，天津自然科学基金(19JCZDJC32600)，天津市高等学校创新团队培养计划(TD13-5035)。

NOTES

^*通讯作者。