1. 引言
模态分析分计算模态分析和试验模态分析。如果模态参数是由有限元计算的方法获得的,则称为计算模态分析;如果是通过传感器和数据采集设备获得输入输出数据,然后通过参数识别获得模态参数,则称为试验模态分析。随着计算机技术的发展,日臻完善的试验模态分析技术,综合了测试技术、信号处理、系统识别和结构动力学分支,并使用模态频率、阻尼和振型等模态参数来描述结构动态特性,使其成为目前对各种工程结构振动进行分析的理想技术 [1] [2] [3]。
本文运用试验模态试验方法对某型号8 × 4载货车转向管路系统模态数据的采集、处理和分析,得到了转向管路系统的振动加速度、固有频率及振型,来判定转向管路系统是否存在共振现象;同时通过载荷谱采集数据和计算模态仿真分析数据进行对比,分析出该转向管路系统固定支架动力特性的特点,验证仿真分析模态准确性,从而为进一步研究转向管路系统振动机理提供了理论基础,利用载荷谱采集数据和有限元分析获得数据来不断改进我们的设计开发工作已经成为汽车行业发展趋势。
2. 计算模态分析
2.1. 有限元分析建模基本原则
1) 需要保证有限元分析精度:
具体措施,一是提高单元阶次,阶次越高,差值函数越能逼近复杂的真实场函数,物理离散精度越高,高阶单元的边界可以是曲线或曲面,因此在离散具有曲线或曲面边界的结构时,几何离散误差也较线性单元小。二是增加单元数量,等同于减少单元尺寸,尺寸减小时,单元的插值函数和边界能够逼近结构的实际场函数和实际边界,物理和几何离散误差都将减小。三是建立和实际相符的边界条件,如果模型边界条件与实际工况相差较大,计算结果就会出现加大误差,这种误差有时甚至超过有限元法本身带来的原理性误差。
2) 适当控制模型规模减少计算强度:
建立几何模型时,并不总是照搬结构的原有形状和尺寸,有时要做适当的简化和变换处理。合理的近似和变换可以降低模型规模,而仍然保持一定的工程精度要求,几何模型的处理方法有:降维处理、细节简化、等效变化、对称性利用和划分局部结构等。
2.2. 有限元建模、简化分析过程
1) 模型简化
为获得高质量的单元,提高计算精度,建模之前需要对3D模型进行一定程度的简化。
一是,取消对结构特性影响较小,但会增加建模工作量和难度的小结构,例如5 mm以下非连接用小孔及5 mm以下折弯圆角等,本文有限元分析把车架、方向机等不参与仿真零部件模型全部简化,二是取消非承载结构,例如厚度在1 mm以下的封板、管线支架、装饰罩等。
2) 网格划分、质量赋予
对于薄壁零部件在进行有限元分析时采取抽中面处理,用来抽中面的零部件形状不会改变,而且会减少计算工作量,提高有限元分析的精度,本文中有限元分析对转向高压钢管、转向油管固定支架采取抽中面处理,抽完中面处理后采用2D网格划分,网格尺寸为4 mm;由于转向钢管中间有液压液压油,为减少仿真难度,提高仿真分析准确性,本文通过增加转向钢管密度的方式,把转向液压油重量加载在转向钢管上,使转向液压钢管内液压油参与仿真计算分析,这样计算仿真环境和转向钢管真实受力环境较为相近;
仿真分析简化后模型如图1。
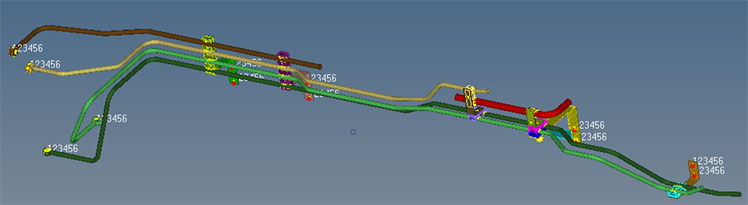
Figure 1. Layout of simplified finite element model for steering piping system
图1. 转向管路系统有限元简化模型布置图
3) 有限元分析结果
本文方向机、车架结构对整个转向管路系统仿真精度影响不大,把上述大件简化掉,同时为了模拟转向钢管为真实连接结构,对转向钢管固定端头采取固定约束进行固定,转向钢管和固定支架之间采取绑定约束,使转向钢管支架网格和附近的转向钢管网格绑定组成一体参与仿真计算,转向管路系统固定支架支撑孔位采取固定约束,模拟真实装配环境;转向管路系统按照有限元分析规范,分别按照X、Y、Z方向各加载5g加速度进行激励。
按照上述模型简化、网格划分、约束及加载激励后,仿真结果如表1:
计算仿真分析前四阶模态分布如图2。
4) 计算有限元分析结果解读
转向管路系统分析流程:把转向系统置于整车中,计算转向系统在整车中的模态频率,对比仿真分析计算值和目标值,如果计算结果满足目标值要求,则转向管路系统满足设计要求,否则需要继续优化,优化方向就是排查转向管路系统置于整车中的薄弱区域,从而改进转向管路系统整体性能。
 一阶模态分布 二阶模态分布
一阶模态分布 二阶模态分布 三阶模态分布 四阶模态分布
三阶模态分布 四阶模态分布
Figure 2. Simulation analysis of the first four order modal distribution
图2. 计算仿真分析前四阶模态分布
目标值设定依据:转向管路系统的模态频率需要避开发动机怠速激励频率,因此要求转向系统设定的目标值需要高于发动机怠速激励频率。
发动机怠速激励频率计算公式:
。
其中n为发动机怠速转速,z为发动机缸数,r发动机冲程数。
根据目前发动机怠速区间及发动机配置,本文分析车型发动机怠速激励频率为在30~35 Hz之间,上述仿真分析转向管路系统一阶频率40.2 Hz和发动机怠速振动频率较近,不能有效规避发动机怠速激励频率,存在共振风险,需要进行设计优化改进。
5) 机械共振
共振是指机械系统所受激励的频率与该系统的某阶固有频率相接近时,系统振幅显著增大的现象。共振时,激励输入机械系统的能量最大,系统出现明显的振型称为位移共振。在一般情况下共振是有害的,会引起机械和结构很大的变形和动应力,如果转向管路系统发生共振,会对整个转向管路系统强度产生非常大的危害,严重时会造成转向管路系统零部件断裂等问题。
3. 载荷谱试验数据
根据计算有限元分析数据,在转向管路系统薄弱位置(有限元分析振动最大位置)设置两路三通道加速度传感器,检测转向管路系统最大加速度值,检测数据加速度分布图如表2:

Table 2. Test data acceleration distribution table
表2. 检测数据加速度分布表
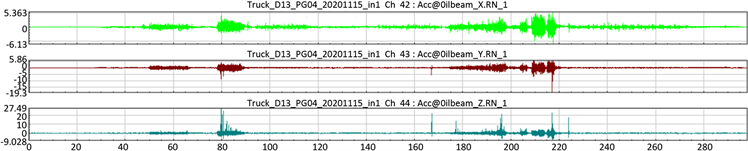
Figure 3. Load spectrum acquisition of the vibration acceleration spectrum of the steering pipe system
图3. 载荷谱采集转向管路系统振动加速度路谱
按照8 × 4载货车在耐久路面采集数据综合分析可知,如果机械零部件振动在10 g以上,零部件所在工况就非常恶劣,这也是我们设计工作中需要尽量避免的情况。
从图3载荷谱数据可知,在耐久路面转向管路支架悬臂外沿Z向加速度较大(检测点2),最大加速度达到31.532 g,存在共振现象,共振会对转向管路固定支架强度产生非常大的危害,而且载荷谱采集数据与计算仿真分析结果一致,计算仿真分析结果具备很强的参考价值,能够作为我们后续设计优化的参考。
4. 转向管路系统设计优化
振动系统的三要素:激励、系统和响应,外界对振动系统的激励或作用称为激励,本文中发动机怠速振动就是最重要的激励源,系统对外界影响的反映称为振动系统的响应 [4] [5]。针对上述模态性能存在问题的原因,经过综合分析,主要从改进转向管路系统刚度来降低对激励源的反映,具体方案在转向管路系统振幅最大位置前方200 mm位置增加一个固定点来提升整个转向管路系统刚度,尽可能减少发动机怠速激励影响,改进后重新对转向管路系统进行有限元分析,改进前后有限元分析模态对比如图4所示。
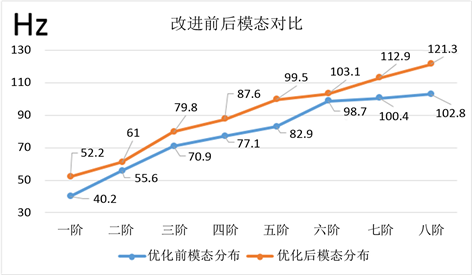
Figure 4. Comparison of modes before and after improvement of steering piping system
图4. 转向管路系统改进前后模态对比
转向管路系统改进后前四阶模态分布如图5。
 一阶模态分布 二阶模态分布
一阶模态分布 二阶模态分布 三阶模态分布 四阶模态分布
三阶模态分布 四阶模态分布
Figure 5. The first four order modal distribution of the improved steering piping system
图5. 转向管路系统改进后前四阶模态分布图
从图5可知,改进后,转向管路系统一阶模态提升到52.2 Hz,能够有效避开发动机怠速激励频率(30~35 Hz),载荷谱重新采集转向管路系统X、Y、Z向最大振动加速度,采集载荷谱数据如图6,其中Z向最大加速度为7.85 g,振幅明显降低,满足小于10 g的要求,达到设计优化目的。
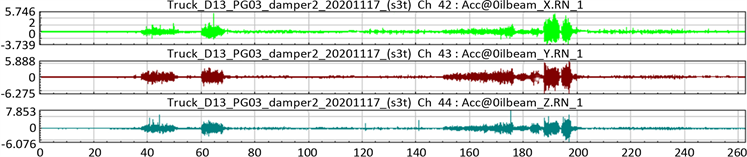
Figure 6. Load spectrum acquisition of the vibration acceleration spectrum of the steering pipe system
图6. 载荷谱采集转向管路系统振动加速度路谱
5. 结论
综上所述,通过计算模态仿真分析数据和载荷谱数据对比,验证我们模型简化、仿真系统约束、零部件设置约束关系等操作后计算仿真分析获得数据准确性较高,仿真结果可以作为我们设计改进的依据。计算模态分析方法具有一定的适用性,可用于对于其他的机械结构的振动模态试验分析的研究,利用好计算模态仿真分析工具对加快我们设计开发工作非常有益。