基于增量矩阵分解的推荐系统研究

Research on Recommendation System Based on Incremental Matrix Decomposition

摘要: 矩阵分解(Matrix Factorization, MF)属于推荐系统中的一种应用广泛且较为经典的算法。它是基于用户行为的推荐算法，被广泛知道的是矩阵分解算法是一种很好的推荐算法。在Netflix Prize算法竞赛中取得了巨大成就，有很多应用矩阵分解拿到冠军的团队，矩阵分解可以有效地解决电影评分预测问题。传统的推荐模型通常采用离线训练的方法，计算出所有训练数据的预测系数用户。在实践中场景中总有一些新用户在训练集中找不到。但我们有他的历史行为记录。那我们对该用户如何进行预测评分呢？最简单的方法是将新用户的数据与旧数据集相结合，再一次进行矩阵分解操作。但是这样的操作计算成本太高了，对于时间成本的要求过高，是行不通的。对于新用户的电影评分预测如何解决这一问题，经过对比分析实验，发现增量矩阵分解算法就可以很好的帮助我们解决新用户电影评分预测的问题，本文将具体阐述如何通过增量更新的方式，大幅度的减少针对新用户电影评分预测的时间，有效的解决新用户进入系统后数据快速更新的问题。每当有新的数据产生，新的用户产品的时候，系统可以快速的对其进行训练，使得模型能够实时应用，优化用户体验。

Abstract: Matrix Factorization (MF) is a widely used and classic algorithm in recommender system. It is a recommendation algorithm based on user behavior. It is widely known that matrix factorization algorithm is a good recommendation algorithm. In the Netflix prize algorithm competition, it has made great achievements, there are many applications of matrix factorization to win the championship team; matrix factorization can effectively solve the problem of film score prediction. Traditional recommendation models usually use off-line training method to calculate the prediction coef-ficients of all training data. In practice, there are always some new users in the scene that can’t be found in the training set. But we have a record of his historical behavior. How do we rate the user? The simplest method is to combine the new user’s data with the old data set and perform matrix decomposition again. But the cost of calculation is too high, and the time requirement is too high. For the new user’s movie score prediction how to solve this problem, after comparative analysis and experiments, it is found that the incremental matrix decomposition algorithm can help us solve the problem of new user’s movie score prediction. This paper will specifically elaborate how to reduce the time of new user’s movie score prediction by means of incremental update, and effectively solve the problem of new user’s entering the system, the problem of data fast updating after the unification. Whenever there are new data and new user products, the system can train them quickly, so that the model can be applied in real time and the user experience can be optimized.

1. 引言

如今时代经济发展迅速，对于消费的定义也发生着变化，消费不断进行着升级，用户需求个性化已经形成一种趋势 [1]。推荐系统可以有效的捕获用户对于关注点的个性化偏好，同时更是可以有效的提升用户满意度，平台的收入也处于大幅上升趋势 [2]。以此为主因开始关注和使用推荐系统的平台也占着大比重。推荐系统对用户的历史显性数据及隐性数据进行分析 [3]，为用户推荐定制化口味的产品。一个受大家认可的个性化推荐可以用户体验大幅度增强，电子商务巨头亚马逊和Netflix已经将推荐系统作为其网站的重要组成部分。推荐系统对娱乐产品，如电影、音乐和电视节目有着特别显著的效果 [4]。每个用户电影口味是不同的，越来越多的客户喜欢自己口味的电影 [5]。事实证明，用户愿意表明他们对特定电影的满意程度，因此可以获得大量关于哪些电影吸引哪些客户的数据 [6]。公司可以通过分析这些数据为用户推荐符合口味的电影。

推荐系统要做的事情就是为每个用户找到其感兴趣的物品推荐给他，做到千人千面。在各种推荐算法中，矩阵分解(Matrix Factorization, MF)是一种经典且广泛应用的算法 [7]，在基于用户行为的推荐算法里，矩阵分解算法有着很好的推荐效果，它通过潜在因子的向量来表征用户和项目 [8]。矩阵分解算法是基于用户历史行为数据的算法，通过用户的历史行为数据，为用户推荐可能感兴趣的物品，预测其对于该物品的评分。

矩阵分解可以十分有效地解决电影评分预测的问题，传统的推荐模型一般是将训练集的数据采用离线的训练方式，全量地进行导入训练，计算出所有用户的预测评分 [9]。在实际的场景中，往往会不断有新的用户出现，在训练集里没出现过，但是我们有他的历史行为数据，那我们如何计算该用户的预测评分呢？最简单的方式就是将这个新用户的数据合并到旧的数据集中，重新做一次矩阵分解 [10] [11]，但是这样子的计算代价太大，在时间上是不可行的 [12]。本文为了解决新用户的电影评分预测问题，根据用户历史行为数据，先固定物品向量，在不重算所有用户向量的前提下，快速计算出新用户向量，这类模型成为增量模型 [13]，因此本文提出的模型称为增量矩阵分解模型。

2. 矩阵分解

矩阵分解，就是把用户和物品都映射到一个K维空间上，这个k维空间不是直接看到的，通常称为隐因子。每一个物品都得到一个向量q，每一个用户也得到一个向量p。对于物品，与它对应的向量q中的元素，有正有负，代表着这个物品背后暗藏的一些用户关注的因素，对于用户，与它对应的向量p中的元素，也有正有负，代表这个用户在若干因素上的偏好。物品被关注的因素和用户偏好的因素，它们的数量和意义是一致的，就是我们在矩阵分解之处人为指定的k。

矩阵分解算法是基于用户行为的算法，为此需要先获取用户的历史行为数据，然后以此为依据去预测用户可能感兴趣的物品 [14]。将收集到的用户行为数据通过矩阵的方式展示出来，矩阵分解算法要做的事情就是去预测出矩阵中所有空白处的评分，并且使得预测评分的大小能反映用户喜欢的程度，预测评分越大表示用于越可能喜欢。这样我们就可以把预测评分最高的前K个物品推荐给用户。

简单来说，矩阵分解算法是把评分矩阵分解为两个矩阵乘积的算法，如图1：

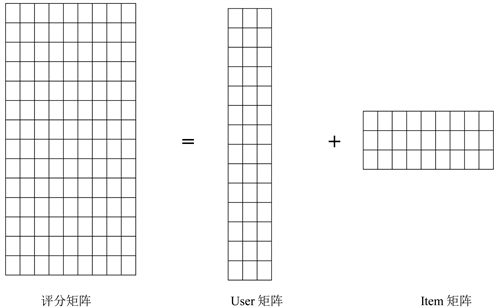
Figure 1. Graphic of matrix decomposition algorithm

图1. 矩阵分解算法图解

在图中，等号的左边是评分矩阵，是已知数据，它被矩阵分解算法分解为等号右边的两个矩阵的乘积，其中一个被称为用户矩阵，另一个被称为物品矩阵。如果评分矩阵有n行m列(即n个用户，m个物品)，那么分解出来的用户矩阵就会有n行k列，其中，第i行构成的向量用于表示第i个用户。物品矩阵则有k行m列，其中，第j列构成的向量用于表示第j个物品。这里的k是一个远小于n和m的正整数。当我们要计算第i个用户对第j个物品的预测评分时，我们就可以用用户矩阵的第i行和物品矩阵的第j列做内积，这个内积的值就是预测评分了。

那矩阵分解是如何从评分矩阵中分解出用户矩阵和物品矩阵的呢？简单来说，矩阵分解把用户矩阵和物品矩阵作为未知量，用它们表示出每个用户对每个物品的预测评分，然后通过最小化预测评分跟实际评分的差异，学习出用户矩阵和物品矩阵。也就是说，图中只有等号左边的矩阵是已知的，等号右边的用户矩阵和物品矩阵都是未知量，由矩阵分解通过最小化预测评分跟实际评分的差异学出来的。评分矩阵可以被矩阵算法分解为如下用户矩阵和物品矩阵的乘积，如下表1。

Table 1. User Item matrix examples

表1. User Item矩阵实例

因为用户向量和物品向量的内积等于预测评分，所以在我们学出用户矩阵和物品矩阵之后，把这两个矩阵相乘，就能得到每个用户对每个物品的预测评分了，评分值越大，表示用户喜欢该物品的可能性越大，该物品就越值得推荐给用户。下面的表2给出了表1中的用户矩阵和物品矩阵相乘的结果，我们把它称为预测评分矩阵，如下表2。

Table 2. Prediction scoring matrix

表2. 预测评分矩阵

矩阵分解算法的输入是用户对物品的评分矩阵，输出是用户矩阵和物品矩阵 [15]，其中用户矩阵的每一行代表一个用户向量，物品矩阵的每一列代表一个物品的向量。用户对物品的预测评分用它们的向量内积来表示，通过最小化预测评分和实际评分的差异来学习用户矩阵和物品矩阵。用矩阵表示即为：

$\tilde{R}=Q{P}^T$

事实上用户的行为数据是一个非常非常稀疏的矩阵 [16]，因为大部分用户只看过全部电影中很少一部分。如何利用这个矩阵去找潜在因子呢？本文主要应用到的是矩阵的UV分解。也就是将上面的评分矩阵分解为两个低维度的矩阵，用Q和P两个矩阵的乘积去估计实际的评分矩阵，而且我们希望估计的评分矩阵R实际的评分矩阵不要相差太多，也就是求解下面的目标函数：

${\hat{r}}_{ui}=\stackrel{\to }{p_{uk}}\cdot \stackrel{\to }{q_{ik}}={\displaystyle \underset{k=1}{\overset{k}{\sum }}{p}_{uk}{q}_{ik}}$

这里涉及到最优化算法，在实际应用中，本文采用梯度下降法就可以求得这P,Q两个矩阵的估计值。对于评分预测我们利用平方差来构建损失函数：

$Cost={\displaystyle \underset{u,i\in R}{\sum }{\left(r_{ui}-{\hat{r}}_{ui}\right)}^2}={\displaystyle \underset{u,i\in R}{\sum }{\left(r_{ui}-{\displaystyle \underset{k=1}{\overset{k}{\sum }}{p}_{uk}{q}_{ik}}\right)}^2}$

加入L2正则化：

$Cost={\displaystyle \underset{u,i\in R}{\sum }{\left(r_{ui}-{\displaystyle {\sum }_{k=1}^k{p}_{uk}{q}_{ik}}\right)}^2}+\aleph \left({\displaystyle \underset{U}{\sum }{p}_{uk}^2}+{\displaystyle \underset{I}{\sum }{p}_{ik}^2}\right)$

梯度下降更新参数，计算出最终的用户向量和物品向量。

3. 增量矩阵分解

在模型训练完以后，就会得到训练集里每个用户的向量和每个物品的向量。在实际的场景中，往往会不断有新的用户出现 [17]，在训练集里没出现过，但是我们有他的历史行为数据，那我们如何计算该用户的预测评分呢？当然，最简单的方法就是把这个用户的行为数据合并到旧的训练集里，重新做一次矩阵分解，进而得到这个用户的向量 [18]，但是这样做计算代价太大了，在时间上不可行。

为了解决训练数据集以外的用户(我们称之为新用户)的推荐问题，我们就需要用到增量矩阵分解算法。增量矩阵分解算法能根据用户历史行为数据，在不重算所有用户向量的前提下，快速计算出新用户向量 [19]。

在梯度下降算法里，当固定 $Q$ 计算Pu时，我们只需要用到用户u的历史行为数据Rui，不同用户之间Xu的计算是相互独立的。这就启发我们，对于训练集以外的用户，我们同样可以用他的历史行为数据以及训练集上收敛时学到的 $Q$，来计算新用户的用户向量。

设用户历史行为数据为Rui，训练集上学到的物品矩阵为 $Q$，要求解的用户向量为Pu，我们可以将用户的历史行为数据Rui以及训练集上学习到的物品矩阵 $Q$，在保证 $Q$ 不变的情况下，通过梯度下降算法，不断收敛得到用户u的用户向量Pu，再通过算法 $Rui=Pu*Q$ 计算出用户对于所有物品的预测评分。

事实上，增量矩阵分解的目标函数中的 $Q$ 也不一定要是矩阵分解在训练集上学出来的，只要 $Q$ 中的每个向量都能表示对应物品的特征就行，也就是说可以是由其他数据和其他算法事先学出来的。

4. 实验分析

4.1. 数据集

本文并没有采用传统的推荐系统评估方式，没有将数据集分为测试数据集以及训练数据集，用训练数据集进行训练，测试数据集进行系统测试。本文主要解决的问题是数据集之外的用户评分预测问题，传统的系统评估方式无法适用。

本文采用的数据样本为mark中用户的行为数据，分别测试将新用户的数据合并到旧的数据集中重新进行矩阵分解以及增量矩阵分解两种方式。数据细节见表3。

Table 3. Mark data

表3. Mark数据

4.2. 实验设置

实验环境见表4。

Table 4. Experimental environment

表4. 实验环境

4.3. 实验结果

本文使用模型更新时间(Update Time)和召回率(Recall)作为实验的评价指标。其中Recall@N表示推荐N个物品时的召回率。实验结果见表5。

Table 5. Experimental result

表5. 实验结果

从实验结果可以看出，本文提出的增量矩阵分解数据更新时间远远低于将数据合并到旧的数据集重新进行矩阵分解这种方式，在实际项目中，也能有很好的用户体验。可以高效的处理当一个新用户来到系统中的个性化推荐问题。

5. 结束语

现推荐系统模型大部分都是采用离线训练的方式 [20]，模型训练完成以后再上线使用，在系统积累了一定的数据之后，或者固定一段时间后再将新的数据合并到旧的数据集中重新进行模型训练 [21]。这样子的方式对于数据的实时性，用户的体验来说是有不太友好的 [22]。本文提出的增量矩阵分解算法在解决数据集之外的新用户的评分预测问题有着很显著的效果，可以有效的解决新用户进入系统后数据快速更新的问题。每当有新的数据产生，新的用户产品的时候，系统可以快速的对其进行训练，使得模型能够实时应用，优化用户体验。