桨式搅拌釜不同桨叶角度下搅拌性能的数值模拟

Numerical Simulation of Stirring Performance of a Paddle Agitator with Different Blade Angles

摘要: 在现有桨式搅拌釜中，针对不同的桨叶角度，运用Fluent软件对搅拌釜内固液混合效果进行数值模拟。通过分析轴截面液相速度矢量图和固含率云图可知，随着桨叶与水平面间角度的增加，底部的固体颗粒沉积越多，减小桨叶与水平面间角度虽然有利于减少底部固体沉积，但同时导致了上部固体颗粒含量较少。考虑整体混合效果，得出桨叶与水平面间角度成30˚时，搅拌釜内固液混合效果最佳。

Abstract: In the existing paddle agitator, the software Fluent was used to simulate the solid-liquid mixing effect in the agitator according to different blade angles. By analyzing the liquid phase velocity vector diagram and solid holdup cloud diagram of the axial section, it can be seen that with the in-crease of the Angle between the blade and the horizontal plane, more solid particles are deposited at the bottom. Although the reduction of the Angle between the blade and the horizontal plane is conducive to the reduction of solid deposition at the bottom, it also leads to the lower content of solid particles at the top. Considering the overall mixing effect, it is concluded that when the Angle between the blade and the horizontal plane is 30˚, the solid-liquid mixing effect in the agitator is the best.

1. 引言

桨式搅拌釜因其操作条件可控范围较大，广泛的应用于生物、化工、食品、制药等多种多样的工业生产过程中 [1]。其通过搅拌桨在液体中旋转，向液体提供能量，促使液体在搅拌釜中作某种循环运动以达到加快传质、反应及热传递的目的 [2]。在桨式搅拌器中，桨叶与水平面间的角度会直接影响搅拌效果，不同角度的桨叶旋转后使搅拌釜内流体产生强度不同的轴向流以及径向流，从而影响搅拌釜内固液两相的混合效果。

计算流体力学(CFD)已经广泛运用于搅拌过程中的流场模拟，实现流场分析的可视化，一定程度上替代了实验，缩短了研究周期 [3]。许卓、赵恒文 [4] 等人运用Fluent软件对桨式搅拌器搅拌桨在不同安装高度的情况进行了数值模拟，模拟了搅拌槽内流场的湍流强度分布、流场速度分布以及搅拌功率大小，结果表明，在合适的安装高度下，搅拌功率随着安装高的增加略微减小。黎义斌、宋亚娟 [5] 等以某搅拌反应器的推进式桨叶为研究对象，通过对四种推进式桨叶内部气液两相流动进行数值分析，实现了推进式桨叶参数设计和性能优化。张晓雨、龙梅 [6] 等对3种安装不同类型桨叶的挡板搅拌槽进行了数值模拟研究，分析并对比不同类型桨叶的固液流动特性，结果表明，PBT6产生轴向流，RT6和FBT6产生径向流，且RT6的搅拌性能优于FBT6。本文针对桨式搅拌釜桨叶与水平角度的变化进行数值模拟，根据数值模拟结果为桨式搅拌釜桨叶角度的选择提供一定的理论依据。

2. 模型建立及网格划分

2.1. 模型建立

本文的主要研究对象是桨式搅拌釜，如图1示，液面高度为2.4 m，桨叶数量为2，安装高度0.8 m，转速N = 100/rpm，桨叶直径为0.6 m。仿真采用的桨叶与水平面间角度分别为15˚、30˚、45˚、60˚、75˚、90˚，搅拌物料为水和二氧化硅颗粒。其中二氧化硅密度为2400 kg/m³，颗粒直径为7.4 μm，体积分数为30%；水的密度为1000 kg/m³，粘度为0.001003 Pa∙s。

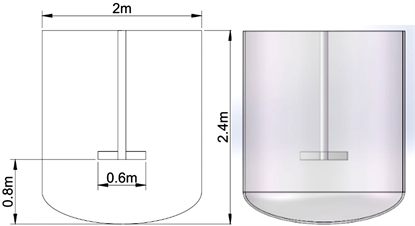
Figure 1. Schematic diagram of paddle agitator

图1. 桨式搅拌釜示意图

2.2. 网格划分

在Solidworks中搭建三维模型，完成后导入DesignModeler进行网格划分前处理。本数值模拟使用多重参考系法(MRF) [7]，以桨叶底部为坐标原点，将桨叶及周围流体设置为动区域，其余部分设置为静区域。由于非结构化网格具有较好的适应性，本文采用了Mesh软件中为整个流体区域生成非结构化网格，对动区域以及桨叶和轴表面进行网格加密处理。在壁面处采用inflaction法生成膨胀层，四面体网格总数量为2,373,998个，其中动区域网格数量为196,933个。整体网格和动区域网格分别如图2和图3所示。

Figure 2. Overall grid

图2. 整体网格

Figure 3. Motion area grid

图3. 动区域网格

3. 数值模拟

3.1. 数值模拟依据

搅拌釜内的流体运动属于三维湍流，具有不规则性，连续性，三维性，耗散性及扩散性。整个釜内的流体应当遵循质量守恒，动量守恒和能量守恒三大基本定律。本文中开展的数值模拟涉及到在湍流情况下的物料混合，严格依照湍流运输方程和遵照组分守恒定律进行。

3.1.1. 质量守恒方程

对于不可压缩流体，质量守恒方又称连续性方程 [8]，其表达式为：

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0$

式中u、v、u分别为速度矢量在x轴、y轴、z轴上的速度分量。

3.1.2. 动量守恒方程

动量守恒方程又称作N-S方程，其表达式为：

$\{\begin{array}{c}\frac{\partial \left(\rho u\right)}{\partial t}+div\left(\rho u\bar{u}\right)=div\left(\mu gradu\right)-\frac{\partial p}{\partial x}+S_u\\ \frac{\partial \left(\rho v\right)}{\partial t}+div\left(\rho v\bar{u}\right)=div\left(\mu gradv\right)-\frac{\partial p}{\partial y}+S_v\\ \frac{\partial \left(\rho w\right)}{\partial t}+div\left(\rho w\bar{u}\right)=div\left(\mu gradw\right)-\frac{\partial p}{\partial z}+S_w\end{array}$ (2)

式中， $\rho$ 为流体密度，t为时间， $\mu$ 为动力粘度， $p$ 为压力。 $S_u$ 、 $S_v$ 、 $S_w$ 是方程的广义源项，其中 $S_u=F_x+S_x$， $S_v=F_y+S_y$， $S_w=F_z+S_z$，其表达为：

$\{\begin{array}{c}{S}_x=\frac{\partial \left[\mu \left(\frac{\partial u}{\partial x}\right)\right]}{\partial x}+\frac{\partial \left[\mu \left(\frac{\partial v}{\partial x}\right)\right]}{\partial y}+\frac{\partial \left(\lambda divu\right)}{\partial x}\\ S_y=\frac{\partial \left[\mu \left(\frac{\partial u}{\partial y}\right)\right]}{\partial x}+\frac{\partial \left[\mu \left(\frac{\partial v}{\partial y}\right)\right]}{\partial y}+\frac{\partial \left(\lambda divu\right)}{\partial y}\\ S_z=\frac{\partial \left[\mu \left(\frac{\partial v}{\partial z}\right)\right]}{\partial x}+\frac{\partial \left[\mu \left(\frac{\partial v}{\partial z}\right)\right]}{\partial y}+\frac{\partial \left(\lambda divu\right)}{\partial z}\end{array}$ (3)

3.1.3. 能量守恒方程

能量守恒方程的表达式为：

$\frac{\partial \left(pT\right)}{\partial t}+\frac{\partial \left(puT\right)}{\partial x}+\frac{\partial \left(pvT\right)}{\partial y}+\frac{\partial \left(pwT\right)}{\partial z}=\frac{\left[\left(\frac{\lambda }{C_p}\right)\cdot \left(\frac{\partial T}{\partial x}\right)\right]}{\partial x}+\frac{\left[\left(\frac{\lambda }{C_p}\right)\cdot \left(\frac{\partial T}{\partial y}\right)\right]}{\partial y}+\frac{\left[\left(\frac{\lambda }{C_p}\right)\cdot \left(\frac{\partial T}{\partial z}\right)\right]}{\partial z}+S_T$ (4)

式中，T为温度， $C_p$ 为比热容， $S_T$ 为粘性耗散。

3.2. 数值模拟设置

如图4所示，本文采用的标准k-ε模型通过求解偏微分方程确定脉动特征速度与平均速度梯度的关系，以耗散尺度作为特征长度 [9]。该模型具有适用范围广，精度合理，收敛性较好等特点。采用多重参考系法可以对动静区域之间的相互作用进行合理处理，将桨叶及其附近定义为动区域，动区域的旋转速度和桨叶旋转速度保持一致。釜体内其余区域设置为静区域，定义该区域流体处于静止。针对该数值模拟，选择稳态计算，当搅拌釜内所有流体参数趋于稳定时该模拟结束，残差收敛值为1 × 10⁻⁴。

Figure 4. k-ε model selection

图4. k-ε模型选择

4. 结果与分析

4.1. 桨叶角度对釜内流体速度场的影响

如图5所示，是六种不同桨叶角度在特定工况下，轴截面(Z = 0 mm)的速度矢量图，其中搅拌桨的桨叶与水平所成角度分别为15˚、30˚、45˚、60˚、75˚、90˚。

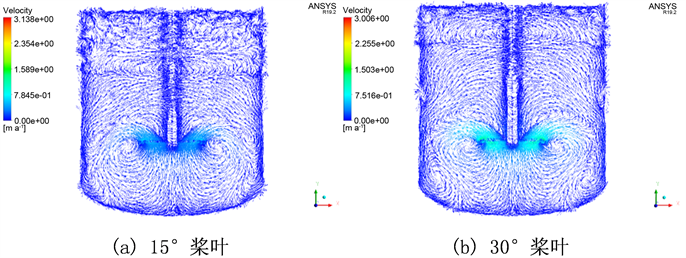
Figure 5. Vectors of liquid phase velocity of axial sections of different blade angles (Z = 0 mm)

图5. 不同桨叶角度轴截面(Z = 0 mm)的液相速度矢量图

根据不同桨叶角度时轴截面(Z = 0 mm)的液相矢量速度图，在该搅拌器工作室，釜内主要产生了轴向流，流体的速度大小沿着桨叶由内向外逐渐变大，在桨叶左右两端处达到最大值。搅拌桨旋转产生动能，该动能从桨叶传递到整个搅拌釜时逐渐减小，导致流体速度也逐渐减小。

桨叶附近的循环流场范围越大，就能带动越多的固体颗粒悬浮，减少釜底部分的固体沉积。结合上图，对比六种角度的桨叶附近的循环流场可以发现，桨叶附近的循环流场范围随着桨叶角度的增大逐渐减小，15˚桨叶周围的循环流场范围最广，90˚桨叶周围的循环流场范围最小。同时，在搅拌釜底部两侧存在两个明显的循环流场，随着桨叶与水平面间的角度提升，这两个循环流场的范围逐渐增大。

搅拌釜通过搅拌桨产生的轴向流将其底部的固体颗粒输送到桨叶上部。15˚桨叶产生的轴向流强度比其他几种桨叶角度产生轴向流强度要小，致使搅拌釜上半部分固体含量较少。综合考虑桨叶提供的轴向流强度和桨叶周围循环流范围，30˚桨叶相较于15˚桨叶提供了更强的轴向流，相比其他更大角度的桨叶其桨叶周围流场范围更大。

4.2. 桨叶角度对固体颗粒浓度分布的影响

如图6所示，是六种不同桨叶角度在特定工况下，轴截面(Z = 0 mm)的固含率云图。

固体颗粒的悬浮状态可以通过固含率云图直观的体现出来 [10]。分析上图可知，随着桨叶角度的变大，底部的固体颗粒沉积明显变多，15˚桨叶搅拌釜底部的固体沉积远小于90˚桨叶底部的固体沉积。得益于桨叶周围较大的循环流场，15˚桨叶有效的减少了搅拌釜底部边缘沉积的固体颗粒，但是由于缺乏强劲的轴向流，在搅拌釜的上半部分固体颗粒较少，达不到固液均匀混合的理想状态。随着桨叶角度的提升，固体颗粒可以随着轴向流流向更高的地方。30˚桨叶相较于15˚桨叶提升了轴向流强度，使得桨叶上部混合效果更佳。同时，30˚桨叶周围的循环流场范围要比更大角度桨叶周围的循环流场范围大，有效的减少了底部固体沉积。

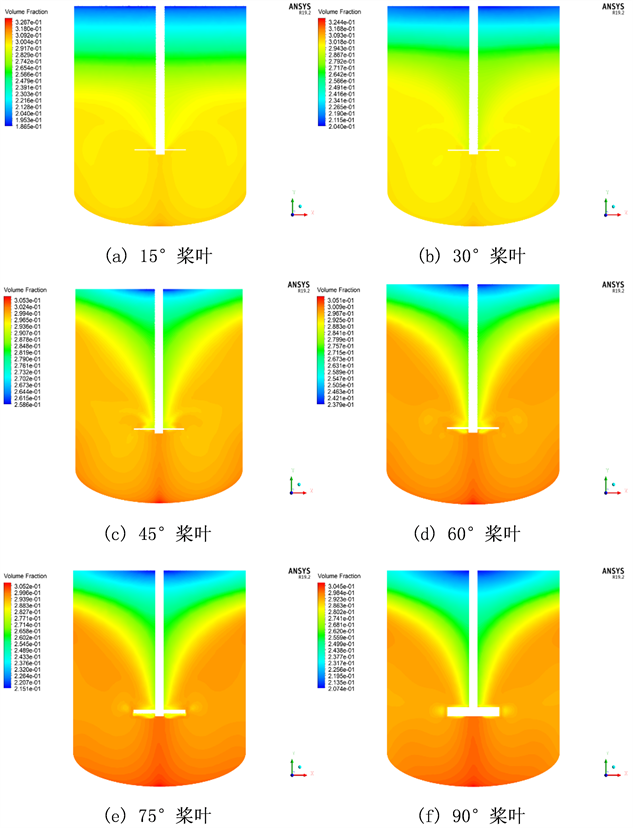
Figure 6. Solid holdup cloud map of axial sections with different blade angles (Z = 0 mm)

图6. 不同桨叶角度轴截面(Z = 0 mm)固含率云图

5. 结语

1) 随着桨叶角度的增大，搅拌桨周围的循环流场辐射范围逐渐减小，不能有效带动釜体底部的固体颗粒参与循环。

2) 随着桨叶角度的增大，固体颗粒的底部沉积越来越多。减小桨叶角度虽然能有效改善固体颗粒底部沉积严重的现象，但是由于缺乏强劲的轴向流，釜内上半部分固体颗粒含量不够理想。

3) 综合考虑整体的混合效果，采用与水平面间角度成30°桨叶时，搅拌釜内固液混合效果最佳。

NOTES

^*第一作者。