磁阻式磁悬浮球形关节的数学建模和分析

Mathematical Modeling and Analysis of Magnetoresistive Magnetic Levitation Spherical Joint

摘要: 为了解决磁阻式磁悬浮球形关节转子转动过程的稳定支承问题，提出一种新型的16齿极转子结构和线圈驱动机制，确保在自旋或偏转过程中转子齿极始终受到两对正交磁悬浮力，为转子提供稳定支承。首先根据电磁作用机制建立定转子之间四个磁悬浮力的力平衡支承模型。然后使用Ansoft有限元软件进行了各种工况和参数下的三维磁场的实验分析，验证了磁阻式磁悬浮球形关节转子的矩角特性和支力–偏角关系，为磁阻式磁悬浮球形关节的稳定悬浮和驱动提供保证。

Abstract: In order to solve the problem of stable support during the rotation of the reluctance magnetic suspension spherical joint rotor, a new type of 16-tooth rotor structure and coil drive mechanism is proposed to ensure that the rotor teeth are always subjected to two pairs of orthogonal during spinning or deflection. The magnetic levitation force provides stable support for the rotor. First, the force balance support model of the four magnetic levitation forces between the stator and the rotor is established according to the electromagnetic action mechanism. Then, we use Ansoft finite element software to carry out the experimental analysis of the three-dimensional magnetic field under various working conditions and parameters, and verify the moment angle characteristics and the supporting force-deflection angle relationship of the reluctance magnetic suspension spherical joint rotor, providing guarantee for the stable suspension and drive.

1. 引言

目前，随着多自由度运动的发展和对简单高效一体化结构的需求，普通的多自由度电机和单自由度球形关节已无法满足，因此磁悬浮球形关节(Magnetic Levitation Spherical Joint)作为多自由运动、控制以及集成化的最佳方案之一被提出 [1] [2] [3] [4]。MLSJ凭借高速，结构简单、集成度高等特点被广泛的应用于机器人、全景摄影操作台以及机械加工中心等方面 [5]。

现有的球形电机定转子上有绕组，结构较为复杂，不利于设备小型化，因此文献 [6] 和文献 [7] 采用永磁体贴片的方式代替转子上的绕组线圈，简化了结构，同时采用等效磁路法确定了磁场分布、得到悬浮力表达式。为了进一步提高转子机械特性，避免永磁式转子的损耗和低效率，文献 [8] [9] [10] [11] 设计了磁阻式的磁悬浮结构，重点进行单绕组设置、简化转子结构从而提高效率；同时文献 [12] 和文献 [13] 设计将硅钢片部分和外壳分开，进一步优化了转子的结构。上述研究多注重转子转矩的变化等问题，未深入讨论运动中转子的稳定性。

本文在前几种文献的基础上进行结构改进，设计了一种16个齿极的转子来配合磁阻式球形磁悬浮关节的定子，并通过矩角特性和支力–偏角关系实现转子稳定支承。

2. 结构和运行原理

本文依据磁悬浮和最小磁阻原理设计的球形关节，其基本结构如图1所示，该关节主要是由定子、转子和混合磁悬浮支撑结构构成。混合磁悬浮支撑结构对转子主要在Z轴方向起承载作用，定转子部分则实现对转子悬浮、转动以及质心偏移的调节作用，通过改变电流大小，实现转子系统在平衡位置高速稳定的支承和旋转驱动。

如图2所示，以自旋状态下A相为例，此时A1、A2、A3、A4这四个磁极绕组通入电流开始工作，由毕奥–萨伐尔定律可知，线圈电流产生磁场，磁场对转子产生悬浮力和转矩。每个磁极的线圈电流分为控制转矩电流和控制悬浮电流，例如A1、A3是X轴方向的一对磁极，向两个定子线圈绕组中通入相同的电流，两组电流产生的径向力同时指向转子的质心，实现X方向的力平衡，Y方向同理。如果转子发生X正方向的偏移，就要通过降低A1磁极的悬浮电流来减弱磁拉力、增强A3位置的悬浮电流扩大磁拉力，控制悬浮合力方向，使转子质心调节回原来位置。本文通过同时控制A1、A2、A3、A4的XY两个方向的4个磁极电流，实现转子受力平衡；通过相序的切换，带动转子旋转，旋转前后受力数量不变。质心未偏移时，四个定子磁极产生的磁场力保持正交方向转子齿极受力相同；当受到外力负载产生质心偏移时，调节对应的磁极，使质心快速回到平衡位置。因此可以得出A相磁极与转子齿极间的气隙中磁场最大，左右两边的B、C相磁极对应的磁场则远小于A相位置的磁场。为了保持转子在Z轴方向的稳定悬浮，通过永磁电磁混合支撑装置来确保定转子之间的可调性，同时简化了转子的夹持装置，使整体结构更加紧凑。

Figure 1. Basic structure of MMLSJ

图1. MMLSJ的基本结构图

Figure 2. Operation principle

图2. 运行原理示意图

3. MMLSJ的数学模型

为了建立MMLSJ的瞬时悬浮力和转矩公式，分析转子受单相绕组产生的主磁场状态。如图2所示主要思路是，将12个磁极划分为A-B-C三相绕组对应的四部分磁导，其中的P1~P4是A相定子绕组通电所产生的四个磁回路，以P2为例，磁回路中包含Pa、Pb、Pc三个磁导，其中Pa是A2相磁极位置的主磁导，Pb、Pc是磁回路上的B2、C1相磁极对应的气隙磁导，Pa处的磁导又可以细分为正对磁极位置的磁导G_g、边缘磁导G_f、漏磁G_d。再通过逆向推导，得出A1~A4所对应的悬浮力和转矩，组成力的平衡方程。

3.1. 气隙磁导表达式

图3为Pa气隙处磁路示意图，各部分的磁导的计算过程是：将气隙磁场分割为若干规则的区域，通过对微小部分的磁导进行积分获得相应区域的磁场，再通过磁场叠加，求出整个的气隙磁场。因此各个部分的磁导为式(1) [14]：

$\{\begin{array}{l}\text{d}{G}_g=\frac{{\mu }_{0}hr}{l_g}\text{d}\theta =\frac{{\mu }_{0}hr}{l_0-\alpha +\frac{\beta \theta }{2}}\text{d}\theta \hfill \\ \text{d}{G}_f=\frac{{\mu }_{0}hr\left(l_0-x_0+\frac{y_0\theta }{2}+2r\theta \right)}{\left(l_0-\alpha +\frac{\beta \theta }{2}+r\theta \right)\left(2l_0-2\alpha +\beta \theta -\pi r\theta \right)}\text{d}\theta \hfill \\ \text{d}{G}_d=\frac{{\mu }_{0}hr}{l_0}\hfill \end{array}$ (1)

其中，气隙磁导Pa = G_g + G_f + G_d，h为硅钢片厚度，r转子质心到齿极的半径，μ₀真空磁导率，l₀平均气隙宽度，θ转角度数，(α，β)是转子从圆心发生偏移的位置。

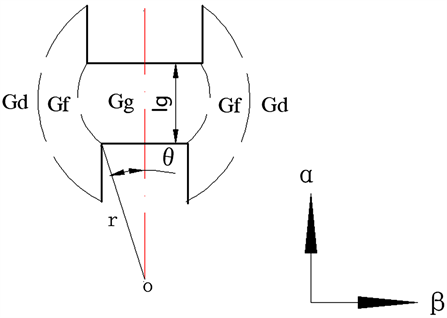
Figure 3. Magnetic circuit division at Pa

图3. Pa气隙处磁路分割

3.2. A2位置的磁通表达式

依据磁路的第二基本方程和文献 [15]，将复杂的磁路进行等效网络，得到如图4所示的等效磁路模型，从而实现Pa位置磁路各部分磁通的近似计算：

$\{\begin{array}{l}{\varphi }_g=G_g{F}_g\\ {\varphi }_a=\left(\frac{R_g+R_f}{R_g}\right){\varphi }_g=\left(1+\frac{G_g}{G_f}\right){\varphi }_g\\ {\varphi }_b=\left(1+\frac{R_{d1}}{R_f}+\frac{R_{d1}}{R_g}\right){\varphi }_g=\left(1+\frac{G_g}{G_{d1}}+\frac{G_f}{G_{d1}}\right){\varphi }_g\\ {\varphi }_c={\varphi }_b+{\varphi }_d=\left(1+\frac{G_g}{G_d}+\frac{G_f}{G_d}\right)\left(1+\frac{G_d}{G_A}\right){\varphi }_g\end{array}$ (2)

其中，F_g、Ф_g、R_g定转子磁极相对处主磁导的磁势、磁通、磁阻，G_f、R_f是边缘位置的磁导、磁阻，G_d1、R_d1为Pa位置漏磁的磁导、磁阻，G_d、R_d为绕组位置漏磁的磁导、磁阻，Ф_c是绕组磁极中的磁通，Ф_b是气隙中的总磁通，N为磁极线圈匝数，I_si是相应线圈通入的电流。

Figure 4. Equivalent magnetic circuit model

图4. 等效磁路模型

3.3. 电感矩阵

忽略铁芯磁饱和的情况下，将Pa位置的磁回路简化，如下图5所示，I_S1、I_S2、I_S3分别是A相、C相、B相通入的电流(由于现在是只有A相中有电流，所以S2、S3都是零)。

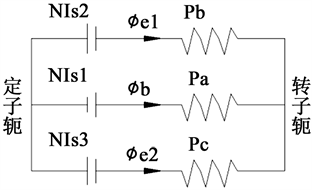
Figure 5. Simplified magnetic circuit diagram

图5. 简化磁路图

结合公式(1) (2)，通过简化磁路图和等效磁路法可以得到以下方程：

$\{\begin{array}{l}{L}_1=\frac{N^2{P}_a\left(P_b+P_c\right)}{P}=\frac{N^2}{P}[\frac{\left(G_{d1}+G_{g1}+G_{f1}\right)\theta {\mu }_{0}hr{F}_g}{N{I}_1{G}_{d1}\left(l_0-\alpha +\frac{\beta \theta }{2}\right)}\ast (\frac{\left(G_{d2}+G_{g2}+G_{f2}\right)\theta {\mu }_{0}hr{F}_g}{N{I}_1{G}_{d2}\left(l_0-\alpha +\frac{\beta \theta }{2}\right)}\\ +\frac{\left(G_{d3}+G_{g3}+G_{f3}\right)\theta {\mu }_{0}hr{F}_g}{N{I}_1{G}_{d3}\left(l_0-\alpha +\frac{\beta \theta }{2}\right)})]\\ L_2=\frac{N^2{P}_b\left(P_a+P_c\right)}{P}=0\\ L_3=\frac{N^2{P}_c\left(P_b+P_a\right)}{P}=0\\ M_{ab}=-\frac{N^2{P}_a{P}_b}{P}=\frac{N^2}{P}\left\{\frac{\left(G_{d1}+G_{g1}+G_{f1}\right)\theta {\mu }_{0}hr{F}_g}{N{I}_1{G}_{d1}\left(l_0-\alpha +\frac{\beta \theta }{2}\right)}\ast \frac{\left(G_{d2}+G_{g2}+G_{f2}\right)\theta {\mu }_{0}hr{F}_g}{N{I}_1{G}_{d2}\left(l_0-\alpha +\frac{\beta \theta }{2}\right)}\right\}\\ M_{ac}=-\frac{N^2{P}_a{P}_c}{P}=\frac{N^2}{P}\left\{\frac{\left(G_{d1}+G_{g1}+G_{f1}\right)\theta {\mu }_{0}hr{F}_g}{N{I}_1{G}_{d1}\left(l_0-\alpha +\frac{\beta \theta }{2}\right)}\ast \frac{\left(G_{d3}+G_{g3}+G_{f3}\right)\theta {\mu }_{0}hr{F}_g}{N{I}_1{G}_{d3}\left(l_0-\alpha +\frac{\beta \theta }{2}\right)}\right\}\\ M_{bc}=-\frac{N^2{P}_c{P}_b}{P}=0\end{array}$ (5)

其中，L₁是定子A相绕组的自感，L₂是定子B相绕组的自感，L₃是定子C相绕组的自感，M_ab是定子绕组AB的互感，M_ac是定子绕组AC的互感，M_bc是定子绕组BC的互感， $P=P_a+P_b+P_c$。由于只有A相通电，BC相绕组没有自感，两相也不会互感，所以L₂、L₃、M_bc都为零。因此，A相绕组的电感矩阵为：

$\left[L\right]=\left[\begin{array}{ccc}{L}_1& M_{ab}& M_{ac}\\ M_{ab}& L_2& M_{bc}\\ M_{ac}& M_{bc}& L_3\end{array}\right]$ (6)

3.4. 电磁悬浮力和转矩表达式

从电机平衡公式推导电磁悬浮力和转矩的表达式，具体是在定子电压方程 $U=IR+LI$ 的两边左乘电流矩阵，求出球形关节的功率方程：

$W=W_r+W_c=I^{2}R+{\left[I\right]}^{\text{T}}L\left[I\right]$ (7)

其中，W_r是电阻发热导致的损耗功率，W_c是磁场储能。

由机电能量转换原理可知，磁场储能可以转换成作用在转子上的XYZ三向的悬浮力在XY方向的分量：

$\{\begin{array}{l}{F}_{A2x}=\frac{\partial W_c}{\partial \alpha }=\frac{1}{2}{I}_1^2\frac{\partial L_1}{\partial \alpha }=\frac{1}{2P}{\left(NI\right)}^2\left[G\frac{\theta {\mu }_{0}hr{F}_g}{N{I}_1{G}_{d1}{\left(l_0-\alpha +\frac{\theta \beta }{2}\right)}^2}-\frac{4}{\theta \beta +2\left(l_0-\alpha \right)}\right]\\ F_{A2y}=\frac{\partial W_c}{\partial \beta }=\frac{1}{2}{I}_1^2\frac{\partial L_1}{\partial \beta }=\frac{1}{2P}{\left(NI\right)}^2[\frac{r\left(\pi -r\right)\ln \left[\theta \beta +\pi \theta r+2\left(l_0-\alpha \right)\right]}{\left(\pi -2r\right)\ast \left(\pi r+\beta \right)\ast \left(2r+\beta \right)}\begin{array}{c}\\ \\ \\ \end{array}\\ +\frac{r\left[\left(\pi -r\right)\beta +4\pi r-8r\right]\theta }{\left[\theta \beta +\pi \theta r+2\left(l_0-\alpha \right)\right]\left(\pi -2r\right)\ast \left(\pi r+\beta \right)\ast \left(2r+\beta \right)}\\ -\frac{r\left[\left(\pi -r\right)\beta +4\pi r-8r\right]\ln \left[\theta \beta +\pi \theta r+2\left(l_0-\alpha \right)\right]\left(\pi r+\beta \right)\ast \left(2r+\beta +1\right)}{\left(\pi -2r\right)\ast {\left(\pi r+\beta \right)}^2\ast {\left(2r+\beta \right)}^2}\\ -G\frac{\theta {\mu }_{0}hr{F}_g\frac{\theta }{2}}{N{I}_1{G}_{d1}{\left(l_0-\alpha +\frac{\theta \beta }{2}\right)}^2}]\end{array}$ (8)

磁场储能对转子自旋角度θ的求偏导，可以得出作用在转子上的电磁转矩表达式：

$\begin{array}{l}{T}_{A2}=\frac{\partial W_c}{\partial \theta }=\left[\frac{{\mu }_{0}hr}{l_0}+\frac{2{\mu }_{0}hr}{2\left(l_0-\alpha \right)+\theta \beta }+\frac{r\left[\left(\pi -2\right)\beta +4\pi r-8r\right]}{\left(\pi -2r\right)\ast \left(2r+\beta \right)\ast \left[\left(\pi r+\beta \right)\theta +2\left(l_0-\alpha \right)\right]}\right]\\ \ast \frac{\theta {\mu }_{0}hr{F}_g}{N{I}_1{G}_{d1}\left(l_0-\alpha +\frac{\beta \theta }{2}\right)}-G\frac{\theta {\mu }_{0}hr{F}_g\theta {\beta }^2}{2{\left(l_0-\alpha +\frac{\theta \beta }{2}\right)}^2}\end{array}$ (9)

由此得到P2位置的悬浮力和转矩的表达式，同理可得另外三处位置的悬浮力分量和转矩。

悬浮力在XY轴方向的合力的公式是：

$\begin{array}{l}{F}_x=F_{A1x}+F_{A3x}+F_{A2x}+F_{A4x}\\ F_y=F_{A1y}+F_{A3y}+F_{A2y}+F_{A4y}\end{array}$ (10)

4. 有限元分析

在工程领域中，Ansoft Maxwell是专门应用于电磁场的有限元仿真软件。根据表1建立MMLSJ的三维物理模型并导入MAXWELL中。在有限元软件中，划分的数量越多，元素长度越小，得到的结果越精细更接近真实状况，然而这势必对运算的资源要求更高，时间更长，因此综合考虑选择设置10,000个划分数量，对变形、不规则的位置增加划分数量，平整无曲折的区域减少划分数量，得到网格图如图6所示。设置A = 0 W/M的边界条件，给定子磁极上的A相线圈绕组通入0.5 A的电流进行仿真，在定转子之间的气隙中间设置半径为56.34 mm的周向磁密观测线。

Table 1. Basic structural material and dimension parameters of MMLSJ

表1. MMLSJ的基本结构材料和尺寸参数表

Figure 6. Grid diagram of 3D model

图6. 三维模型的网格图

图7是定转子气隙中的不同半径的周向路径磁密图。通过气隙中的周向路径磁密观测线可以看出，磁密线的半径(54~58 mm)从转子磁极到定子磁极(包含整个气隙)，有部分位置呈现红色凸起，越靠近定子磁极突出红色现象越明显，且最高幅值达到了0.286 T，造成这种现象的原因是定子磁极处的磁密最强，磁场最大，极易发生磁饱和的现象；而较远处由于磁漏等现象，磁密不如定子磁极处，但整体变化趋势呈平稳。

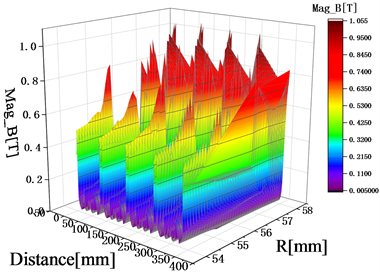
Figure 7. Magnetic density map of air gap at different positions

图7. 气隙不同位置磁密图

图8是不同转角对应的不同位置的气隙路径的磁密值。从图8中可以看出有五个红色凸起，磁密观测线是一个封闭的圆圈，所以第一个和最后一个凸极是重合的，因此，共有四个红色凸起(后面的情况类似，不再重复解释)，底部有数个蓝色小凸起，其值在0.01~0.02 T之间，这是由于A相线圈通电，其对应的转子磁极处的磁密达到最大值为0.0874 T，使转子在正交方向受力相同，保持悬浮力的平衡；底部的蓝色凸起则是相邻转子齿极的磁密，其值在0.02 T左右，符合工作要求。

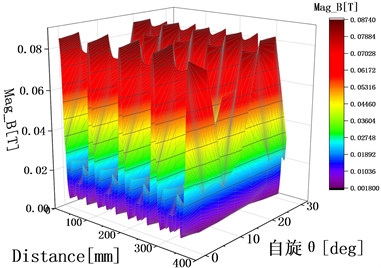
Figure 8. Magnetic density diagram of different rotation angles

图8. 不同转角的磁密图

图9显示的是在A相电流的改变下，气隙中的磁密变化情况。图中显示随着通入电流的增加，整体呈明显的开口向下圆弧形上升趋势，说明磁场的大小主要是由定子磁极线圈中电流决定的，线圈电流越大产生的磁密越强，通过转子的磁力线越多，对转子的悬浮力和转矩的作用越大，然而电流太大通常会损坏线圈绝缘体，而机械受损则可能导致短路。因此，为保证球形关节平稳运行，合理的设计其结构，最终设置线圈匝数为318匝、通入电流为0.5 A。

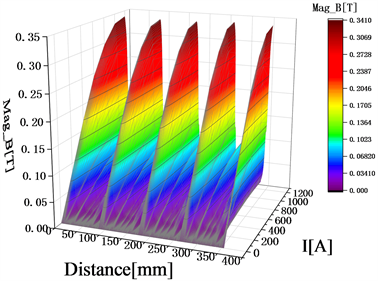
Figure 9. Magnetic density diagram of phase A current

图9. A相电流磁密图

从图7~9的三维磁密变化与运行原理中的分析相同，以定转子中线对齐位置为起始，A1~A4相位置对应的气隙中存在的磁密最高，其余B、C相与转子齿极间的对齐面积小、磁密很低，所以在三幅图中大都处于最低的磁密区间内，与峰值相比几近忽略。符合设计情况。

结合悬浮力公式(8)和图10可知，当转角从θ₁转到θ₃之间，电感与电磁力总体呈正相关，即电感下降的同时导致悬浮力不断下降；由于忽略了磁漏、磁滞以及磁饱和等原因，线性化的电感在θ₁到θ₃之间存在一段恒定电感，仿真图则不存在。同理根据转矩公式(9)可知，转矩的变化是因电感决定的，而电感的曲线呈余弦变化，θ₁处绕组电感最大、磁通最多、磁阻最小，所以转矩是正弦的变化曲线，与下图11的悬浮力和转矩变化图吻合。

Figure 10. Linear inductance curve

图10. 线性电感曲线

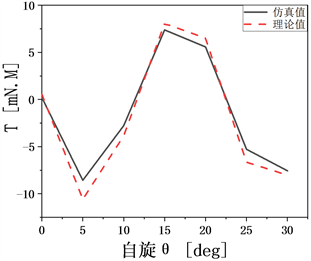(a) (b)

Figure 11. The levitation force and torque of the rotor with the change of spin θ. (a) Chart of levitation force variation; (b) Torque change diagram

图11. 自旋θ变化下，转子的悬浮力和转矩。(a) 悬浮力变化图；(b) 转矩变化图

以A1相为例，通入0.5A的绕组电流进行有限元仿真得到如图11所示。图11(a)中的悬浮力随着角度的增大，悬浮力随之下降，当转角为零时，悬浮力为17.5 mN；当转角为15˚时悬浮力2 mN左右，最终在5 mN的区间上下波动，这是由于开始的位置是A相线圈通电的位置，此处正是定转子磁极相对的地方，磁密最大且悬浮力最强。而在20˚产生上升的原因是该位置对应着一个转子齿极与相邻的磁极有磁通形成回路存在磁场。因此悬浮力大小主要受电流产生的主磁场的影响，离磁极位置越远，悬浮力就下降的越快。为了确保转子齿极在自旋和偏转两个状态受力稳定，当A1相的磁极处悬浮力与A3、A2和A4的磁极悬浮力变化相同，因此A1~A4在XY轴分量上的悬浮力相同，保持支承平衡。图11(b)是转矩图，表示了转子随着转角的变化所受到的旋转力矩的变化，由于受到转子特殊结构的影响，转角的范围在0˚~22.5˚之间。从图中可以明显看出，仿真转矩值最大为8 mN∙m左右，最小为−8 mN∙m左右。通过公式(9)得到的转矩数据表与Maxwell有限元进行虚位移计算仿真得到的数据对比，在电流0.5 A的设置下发现两者的波形相同，两者相差最大值为2 mN∙m，符合设计要求。

图12是转子转动过程中不同电流产生的悬浮力。蓝色曲线虽然电流最大为1200 A (安匝数与实际电流的乘积，以下相同)，但是产生的悬浮力并不是最大的，反而低于800 A、1000 A的曲线，这是由于1200 A已经超过其最大电流值，磁极已经达到饱和状态，超出了控制。各个曲线的整体运动趋势相似，再结合各曲线的平缓程度，可以选择电流600~800 A是一个比较适合区间，既能保持悬浮力在一定高位区间，不至于太低；也可以保证悬浮力的变化波动不会太大，避免转子转动过程中发生偏移和振动。

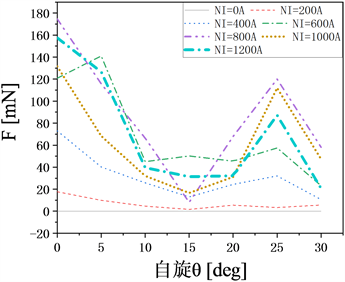
Figure 12. Variation of levitation force at spin angle

图12. 自旋角度下的悬浮力变化

图13是不同电流下的转矩变化，与悬浮力不同的是，在0~1200 A的电流区间，转矩随着电流的增大而增大，在自旋为0的位置，此时的转矩为零，这是由于转子的磁极中线与定子磁极的中线相重合，此时的磁通量达到最大，磁阻最小。在5˚和15˚左右转矩达到最大值150 mN∙M，这是因为转子磁极处于定子磁极之间的位置，磁通量最小，因此转矩达到了最大。

Figure 13. Torque variation at spin angle

图13. 自旋角度下的转矩变化

5. 结论

提出一种新型的16齿极转子结构和线圈驱动机制，根据电磁作用机制建立四个磁悬浮力的力平衡支承模型，确保在自旋或偏转过程中转子齿极始终受到两对正交磁悬浮力，为转子提供稳定支承。通过有限元软件进行了各种工况和电流转角参数下的三维磁场、力和转矩的分析，确定四个主磁场的存在以及磁场对转子齿极的正交磁悬浮力、转子的矩角特性的影响，为磁阻式磁悬浮球形关节的稳定悬浮和驱动提供保证。