能量密度对反射式聚光光伏系统电学特性的实验研究

Experimental Analysis of Energy Density on Electrical Characteristics of Reflective Concentrator Photovoltaic System

摘要: 本文搭建了一套户外反射式聚光光伏系统，并基于光伏电池的单二极管等效电路，建立了InGaP/InGaAs/Ge三结砷化镓聚光光伏模组的数学模型，研究了模组温度为323 K，能量密度为350~500 kW/m2时的反射式聚光光伏系统的基本电学特性，并将实验计算值与理论计算值进行了对比分析。研究结果表明：峰值功率随着能量密度的增加而线性增加，而填充因子与转换效率随着能量密度的增加而减小。当模组温度为323 K，能量密度从350 kW/m2增长到500 kW/m2时，三结砷化镓聚光光伏模组的峰值功率从7.088 W增加到9.589 W，而填充因子从0.816下降到0.786，转换效率从31.64%下降到29.97%。

Abstract: Based on the equivalent circuit of the single diode, the mathematical model of the InGaP/InGaAs/Ge triple-junction solar cells photovoltaic module is established, a set of reflective concentrating pho-tovoltaic system is built. The electrical characteristics of the reflective concentrating photovoltaic system are studied when the module temperature is 323 K and the energy density is 350~500 kW/m2, and the experimental results are compared with the theoretical values. The research results show that the peak power increases linearly with the increase of energy density, while the fill factor and conversion efficiency decrease with the increase of energy density. When the module temperature is 323 K and the energy density increases from 350 kW/m2 to 500 kW/m2, the peak power of the InGaP/InGaAs/Ge triple-junction solar cells photovoltaic module increases from 7.088 W to 9.589 W, while the fill factor decreased from 0.816 to 0.786, and the conversion efficiency decreased from 31.64% to 29.97%.

1. 引言

随着当今世界经济的不断发展以及工业化程度的不断提高，有限的化石能源的消耗逐年增大。过度的化石能源的开采及使用，造成了环境污染及生态破坏，由此产生了能源安全问题 [1]。在当前的能源局势下，研究开发利用可再生能源无疑是一种很好的选择。近年来，太阳能发电技术成为了可再生能源领域发展最快的研究领域之一，其中聚光光伏发电技术迎来了巨大的发展机遇 [2] [3] [4]。

聚光光伏发电系统是指利用光学器件将分散的太阳光汇聚到一块面积很小的电池上，然后通过光生伏特效应将太阳光转化成电能 [5] [6] [7]。经聚光器投射到电池表面的辐照强度是未聚光的太阳能电池的200~1000倍，大大提高了单位面积太阳能电池的输出功率 [8]。

国内外有关学者对聚光光伏系统及其理论计算模型进行了大量的研究：Mintairov等人 [9] 研究了InGaP/InGaAs/Ge三结太阳能电池与GaInP/GaAs双结太阳能电池在高倍聚光比下的I-V特性。研究结果表明在聚光比超过1000倍时，电池的开路电压随着光生电流密度的增加而减小，双结太阳能电池的开路电压下降约为三结太阳能电池的2/3。Tzu-Hsuan Huang等人 [10] 研究了单结、双结、三结砷化镓太阳能电池的转换效率随温度的变化关系。研究结果表明，太阳能电池的转换效率随着电池温度的升高而下降，其中三结砷化镓太阳能电池的温度性更好，其温度系数为−0.0152%/℃。Aho等人 [11] 在实验室内对三结砷化镓电池的温度系数进行了研究，研究结果表明在电池温度为80℃时，开路电压、短路电流和转换效率的温度系数分别为−7.5 mV/℃、0.04 mA/cm²/℃和−0.09%/℃。马帅旗等人 [12] 基于单二极管等效电路模型，利用Matlab研究了不同光照、不同温度时太阳电池的输出特性并与电池厂家提供的I-V特性曲线进行了对比，该模型的输出特性曲线与厂家提供的输出曲线基本一致，验证了该模型的有效性。刘默等人 [13] 基于单二极管模型利用Simulink对CIMJ三结聚光太阳能电池的输出特性进行了研究，研究结果表明开路电压随着温度的升高而减小，随着聚光比的增加呈对数形式增加。转换效率随着聚光比的增加呈现出先增加后减小的趋势，在聚光比为450倍时，转换效率最大为32.93%。Ataser等人 [14] 利用解析太阳能电池模型计算了200~450 K温度范围内AM1.5G太阳光谱的GaInP/GaInAs/Ge三结太阳电池的开路电压和转换效率。结果表明：太阳电池在1个太阳下298 K时的转换效率为35.114%。

目前聚光光伏系统采用的多是折射式聚光器，一般为菲涅尔聚光器，该聚光器普遍存在光学设计简单，聚光效果不明显等缺点，导致聚光系统的效率降低 [15]。文献 [9] [10] [11] 在室内条件下对三结砷化镓电池进行了实验研究，虽然其实验结果可以反映出太阳电池在不同条件下的变化趋势，但是模拟光源与实际太阳光存在着一定的差别，因而其结果并不能真实反应出电池在实际工况下的工作特性。文献 [12] [13] [14] 为利用数学模型对三结砷化镓太阳能电池进行了仿真与理论计算，但是缺乏与实验的对比分析。

综上，本文基于单二极管等效电路模型，建立了InGaP/InGaAs/Ge三结砷化镓聚光光伏模组的数学模型，并基于户外搭建的反射式聚光光伏系统进行实验研究，着重分析了能量密度对InGaP/InGaAs/Ge三结砷化镓聚光光伏模组的峰值功率、填充因子以及转换效率等电学特性的影响，并与理论计算值进行了对比，分析产生误差的原因，为进一步提高聚光光伏系统的效率提供一定的经验。

2. 实验系统

2.1. 反射式聚光光伏系统

图1为本文搭建的反射式聚光光伏系统，该系统位于上海理工大学动力二馆楼顶。系统中发电模组采用的是边侧型聚光光伏发电模组，模组中的聚光镜采用反射式设计。入射后的光线经反射式聚光器反射聚光，聚集到位于模组两侧的三结砷化镓光伏电池上，此装置的光能利用率高达98%，有效地克服了菲涅尔透镜聚光技术透过率低的缺陷(85%以下)。聚光光伏电池采用的是InGaP/InGaAs/Ge三结砷化镓聚光光伏电池，该电池与普通晶硅电池相比具有温度特性好，效率高等优点，目前三结砷化镓光伏电池的最高转换效率达到了44.4% [16]。跟踪控制系统采用双轴太阳能自动跟踪系统，主要由阳光传感器、步移电机、直射辐射表组成。系统运行时，阳光传感器将接收到的光信号转换成电信号传送到控制箱内的PLC控制系统然后经过信号处理传递给步移电机控制其实时精确追踪太阳，达到高倍聚光目的。直射辐射表主要作用是验证聚光光伏系统是否精确追踪太阳。当光斑位置恰好位于标准孔时，说明跟踪系统精确追踪太阳。

Figure 1. Reflective InGaP/InGaAs/Ge triple junction concentration photovoltaic system

图1. 反射式InGaP/InGaAs/Ge三结砷化镓聚光光伏系统

2.2. 实验方法与测量设备

搭建的反射式聚光光伏系统性能测试系统如图2所示。

Figure 2. Reflective concentrating photovoltaic system performance test system diagram

图2. 反射式聚光光伏系统性能测试系统图

3. 三结砷化镓光伏电池的数学模型

图3为三结砷化镓电池的单二极管等效电路模型。

Figure 3. Single diode equivalent circuit model of the cell

图3. 电池的单二极管等效电路模型

电流总的电流密度可表示为：

$I_L=I_{sc}-I_o\left({\text{e}}^{\frac{q\left(V+I_L{R}_s\right)}{n{k}_{B}T}}-1\right)-\frac{V+I_L{R}_s}{R_{sh}}$ (1)

$I_o=k{T}^{\left(3+\frac{\gamma }{2}\right)}{\text{e}}^{-\frac{E_g}{n{k}_{B}T}}$ (2)

$E_g=E_g\left(0\right)-\frac{\alpha T^2}{T+\sigma }$ (3)

式中：I_L、I_sc、I_o分别为电池电流、短路电流和暗饱和电流；q为电子电荷；V为电池电压；k_B为玻尔兹曼常数；R_s、R_sh分别为串联电阻和并联电阻；E_g为禁带宽度；k和n为常数；α和σ为材料参数。

忽略并联电阻，则根据公式(1)可得出电池电压的表达式为：

$V=\frac{n{k}_{B}T}{q}\left[\ln \left(\frac{I_{sc}-I_L}{I_o}+1\right)\right]-I_L{R}_s$ (4)

式中， $R_s=R_{s,1}+R_{s,2}+R_{s,3}$。

当I_L = 0时，由式(4)可得开路电压的表达式为：

$V_{oc}=\frac{n{k}_{B}T}{q}\ln \left(\frac{I_{sc}}{I_o}+1\right)$ (5)

光伏电池的填充因子FF是指光伏电池峰值功率与开路电压及短路电流乘积的比值，用符号FF表示。填充因子按下式定义：

$FF=\frac{P_m}{V_{oc}{I}_{sc}}$ (6)

式中：P_m为峰值功率。

光伏电池的转换效率h为电池峰值功率P_m与入射功率P_in之比：

$\eta =\frac{P_m}{P_{in}}=\frac{P_m}{A{E}_{d}C}$ (7)

式中：C为聚光倍数；A为电池面积；E_d为直射辐照强度。

光伏电池能量密度指单位面积的直射辐照强度与聚光倍数的乘积，即：

$E=C\times E_d$ (8)

式中：E为能量密度。

在聚光条件下，聚光太阳电池的光生电流与入射光的辐照强度之间存在一定的线性关系。假设光生电流与聚光倍数成正比，则聚光倍数可定义为：

$C=\frac{I_{sc}}{I_{sc,1sun}}$ (9)

式中：I_sc,1sun为未聚光时太阳电池的短路电流。

本文采用均方根误差(RMSE)来分析理论值和实验值之间的误差，即：

$e_{\text{EMS}}=\sqrt{\frac{1}{nm}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{m}{\sum }}{\left(\frac{X_{ij}-{\tilde{X}}_{ij}}{{\tilde{X}}_{ij}}\right)}^2}}}$ (10)

式中： ${\tilde{X}}_{ij}$ 、X_ij分别为理论值、实验值。

4. 结论与分析

4.1. 峰值功率

三结砷化镓聚光光伏模组的峰值功率随能量密度的变化如图4所示。由图4可知，在模组温度为323 K时，峰值功率随着能量密度的增加呈线性增加。当能量密度从350 kW/m²上升到500 kW/m²时，峰值功率的实验值从7.088 W增加到9.589 W，而其理论值从7.497 W增加到10.871 W。这是因为随着能量密度的升高，太阳光子通量成倍增加，从而让更多的光子能量被半导体材料吸收，产生更多的载流子使得短路电流随着能量密度的增加而线性增加。此外，由公式(5)可知，开路电压随着能量密度的增加呈对数增加。能量密度的增加使得短路电流与开路电压均变大，进而使得聚光光伏模组的峰值功率与峰值电压增加，因此峰值功率随着能量密度的增加而增加。实验值均小于理论值，峰值功率的实验值与理论值的均方根误差从350 kW/m²时的5.45%增长到500 kW/m²时的11.79%。这主要是由于串联电阻随着能量密度的增加而增加，从而导致串联电阻对电池性能的影响越来越显著，导致其误差相对较大。此外，由文献 [17] 可知，开路电压的温度系数随着聚光比的增加而减小，而在理论计算时将开路电压的温度系数设为定值，这也是误差随能量密度增大的原因之一。

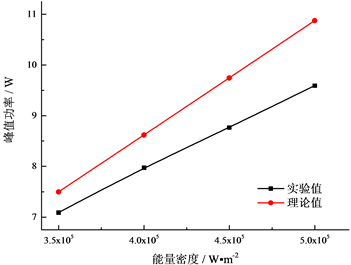
Figure 4. The peakpower of the three-junction concentrating photovoltaic module changes with the energy density

图4. 三结砷化镓聚光光伏模组的峰值功率随能量密度的变化

4.2. 填充因子

三结砷化镓聚光光伏模组的填充因子随能量密度的变化如图5所示。由图5可知，在模组温度为323 K时，填充因子随着能量密度的增加而降低。当能量密度从350 kW/m²上升到500 kW/m²时，填充因子的实验值从0.816下降到0.786，而其理论值从85.54%下降到82.64%。这是因为在聚光条件下，串联电阻的影响加剧，由公式(4)可知，电流流过串联电阻的压降为I_LR_s，降低了负载两端的电压，从而引起填充因子下降。实验值均小于理论值，填充因子的实验值与理论值的均方根误差从350 kW/m²时的4.64%增长到500 kW/m²时的4.86%。这是因为随着串联电阻随着能量密度的增加而增加，串联电阻的增大是引起误差增大的主要原因 [18]。

Figure 5. The fill factor of the three-junction concentrating photovoltaic module changes with the energy density

图5. 三结砷化镓聚光光伏模组的填充因子随能量密度的变化

4.3. 转换效率

三结砷化镓聚光光伏模组的转换效率随能量密度的变化如图所示。由图6可知，转换效率随着能量密度的增加而降低。当能量密度从350 kW/m²上升到500 kW/m²时，转换效率的实验值从31.64%下降到29.97%，而其理论值从33.47%下降到32.87%。这是因为串联电阻会降低等效电路中的短路电流以及负载两端的电压，从而导致光伏电池转换效率的减小。实验值均小于理论值，转换效率实验值与理论值的均方根误差从350 kW/m²时的5.45%增长到500 kW/m²时的8.84%。当能量密度从350 kW/m²上升到500 kW/m²时，均方根误差逐渐加大，这会因为在高倍聚光条件下，投射到聚光光光伏电池表面的能量分布是不均匀的，能量密度越大，电池中心与边缘的光照强度的差异就越大，因此导致转换效率下降的幅度加剧，这是误差增大的主要原因。此外，随着能量密度的增加，电池内部的复合过程趋于复杂化，再加之随着能量密度的增加，聚光电池的物理参数会发生变化，进而导致其误差相对较大。

Figure 6. The efficiency of the three-junction concentrating photovoltaic module changes with the energy density

图6. 三结砷化镓聚光光伏模组的转换效率随能量密度的变化

5. 结论

本文搭建了一套户外反射式聚光光伏系统，并基于光伏电池的单二极管等效电路，建立了InGaP/ InGaAs/Ge三结砷化镓聚光光伏模组的数学模型，着重分析了InGaP/InGaAs/Ge三结砷化镓聚光光伏模组在电池温度为323 K，能量密度为350 kW/m²、400 kW/m²、450 kW/m²、500 kW/m²时的电学特性，并将理论计算值与实验计算值进行对比分析，研究结果表明：

1) 温度一定时，三结砷化镓聚光光伏模组的峰值功率随着能量密度的增大而增大，而填充因子和转换效率随着能量密度的增大而减小。当模组温度为323 K，能量密度从350 kW/m²上升到500 kW/m²时，三结砷化镓聚光光伏模组的峰值功率从7.088 W增加到9.589 W，而填充因子从0.816下降到0.786，转换效率的实验值从31.64%下降到29.97%；

2) 理论计算值与实验计算值存在着一定误差，且理论计算值与实验计算值之间的均方根误差随着能量密度的增大而增大。当模组温度为323 K时，能量密度从350 kW/m²上升到500 kW/m²时，峰值功率的均方根误差为从5.45%增长到11.79%，填充因子的均方根误差从4.64%增长到4.86%，转换效率的均方根误差从5.45%增长到8.84%。